简介
- 二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
- 我们已知二分查找是有序的,为了方便讲解,这次我以一种升序的序列为例进行讲解。
问题解决
溢出问题
在循环体中,一般计算中间值middle时所用的是:
middle=(left+right)/2;但是这种情况容易溢出,因为一旦left+right超过所在类型的范围的话,就会出现错误,为了不出现这种问题,我们引入了:
middle=left+(right-left)/2;边界问题
循环体外的初始化条件,与循环体内的迭代步骤, 都必须遵守一致的区间规则,也就是说,如果循环体初始化时,是以左闭右开区间为边界的,那么循环体内部的迭代也应该如此.如果两者不一致,会造成程序的错误。
左闭右开区间类似[left,right)
while (left < right)
{
middle = (left + right) / 2;
if (list[middle] = target)
{
printf("已找到该值,数组下标为:%d\n", middle);
return list[middle];
}
else if (list[middle] > target)
{
right = middle;
}
else if (list[middle] < target)
{
left = middle + 1;
}
}左闭右闭区间[left,right]
while (left <= right)
{
middle = (left + right) / 2;
if (list[middle] = target)
{
printf("已找到该值,数组下标为:%d\n", middle);
return list[middle];
}
else if (list[middle] > target)
{
right = middle-1;
}
else if (list[middle] < target)
{
left = middle + 1;
}
}最终代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
int binary_search(int* list, int len, int target)
{
int left = 0;
int right = len - 1;
int middle;
while (left < right)
{
middle = (left + right) / 2;
if (list[middle] = target)
{
printf("已找到该值,数组下标为:%d\n", middle);
return list[middle];
}
else if (list[middle] > target)
{
right = middle;
}
else if (list[middle] < target)
{
left = middle + 1;
}
}
printf("未找到该值!");
return -1;
}
int main()
{
int a[] = { 1,4,5,6,9,10,18,23 };
int ret = binary_search(a, sizeof(a) / sizeof(int), 5);
printf("ret=%d\n", ret);
system("pause");
return 0;
}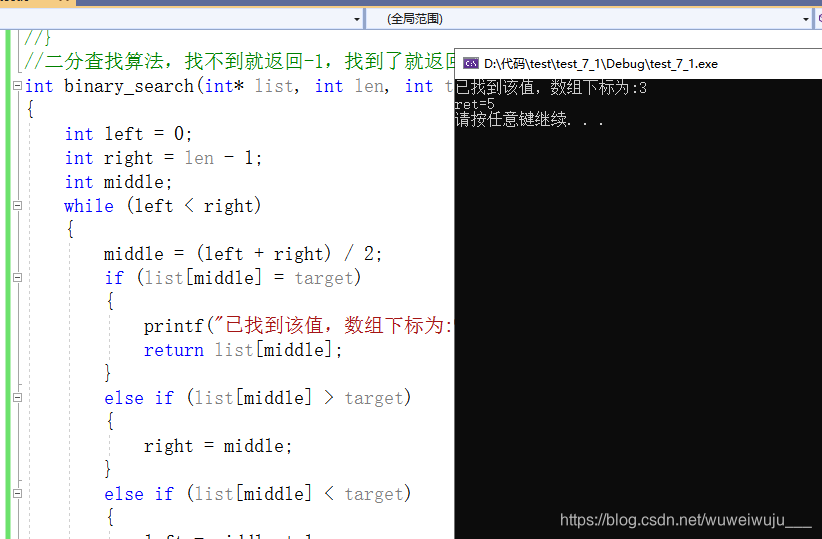





 本文深入解析二分查找算法,探讨其在升序序列中的应用,包括解决溢出问题的技巧和边界条件的处理,附带完整代码示例。
本文深入解析二分查找算法,探讨其在升序序列中的应用,包括解决溢出问题的技巧和边界条件的处理,附带完整代码示例。

















 1731
1731

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










