【数据结构九】二叉树

二叉树：如果树中的每个节点最多只有两个子节点，这样的树就称为二叉树。

所有的树本质上都可以使用二叉树模拟出来。

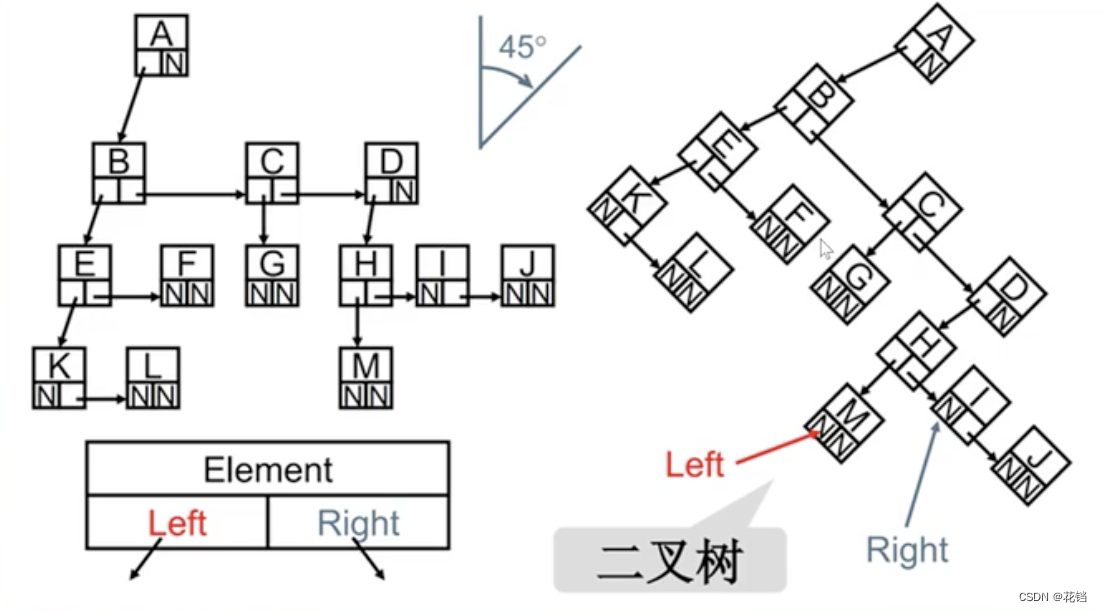
上面的例子并不是二叉树，将它用儿子-兄弟表示法表示，并旋转 45 度，就可以看到模拟成了一颗二叉树。

二叉树的特性：

1. 一个二叉树的第 i 层的最多有 2^(i - 1)，i >= 1 个节点。第 1层最多有 1 个节点，第 2 层最多有 2 个节点，第 3 层最多有 4 个节点…
2. 一个深度为 k 的二叉树最多有 2 ^ k - 1，k >= 1 个节点。第 1层最多有 1 个节点，第 2 层最多有 3 个节点，第 3 层最多有 7 个节点…
3. 对于任何非空二叉树，如果用 n0 来表示叶子节点的个数，用 n2 来表示度为 2 的节点的个数，那么 n0 = n2 + 1。

完美二叉树（满二叉树）：

完美二叉树（满二叉树）：对于一棵二叉树，假设其深度为 d，除了第 d 层外，其余各层的节点都有左右两个子节点，且叶子节点都处在第 d 层。

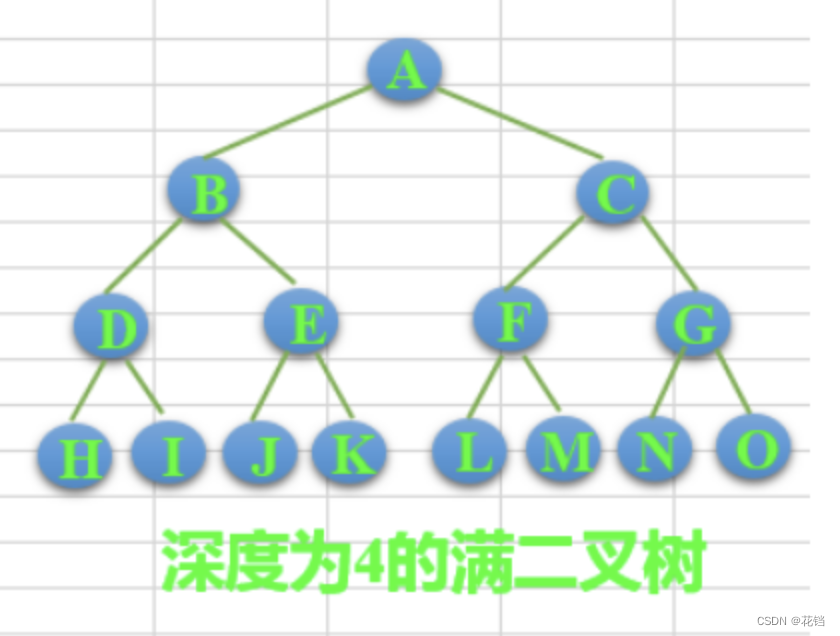
完全二叉树：

完全二叉树：对于一棵二叉树，假设其深度为 d，除了第 d 层外，其余各层的节点数都已达到最大值，且第 d 层的叶子节点从左到右连续存在（也就是说，即使缺少节点，也只能缺少右侧的节点，从左到右必须是连续的）。

完美二叉树是特殊的完全二叉树。

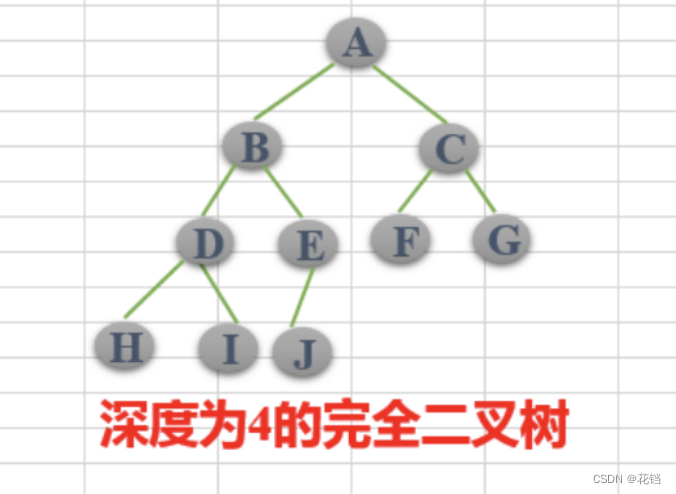
二叉搜索树（BST、Binary Search Tree、二叉排序树、二叉查找树）：

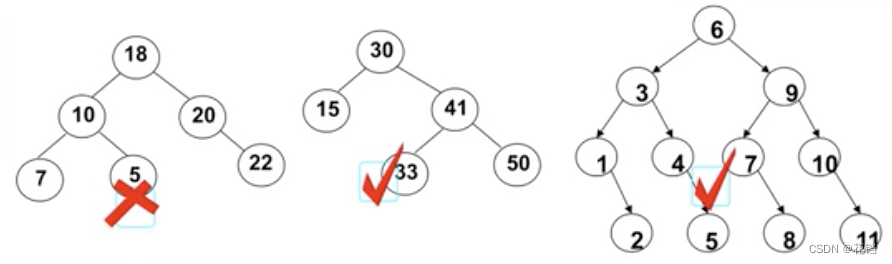
二叉搜索树：不管是哪个节点，它的左子树的节点的值都小于它，右子树的节点的值都大于它。

二叉搜索树的特点就是相对较小的值总是保存在左节点上，相对较大的值总是保存在右节点上，这一特性使得查找的效率非常高。

二叉搜索树的优缺点：

优点：可以快速地找到给定关键字的数据项，并且可以快速地插入和删除数据项。

二叉搜索树查找的方式就是二分查找的思想，效率非常高。

缺点：如果插入的数据是连续的，那么就会导致树的不平衡，那么查找、插入等操作的效率就会变低。

二叉搜索树查找的最大次数就是树的深度，查找到最后一层一定会有一个存在或者不存在的结果。

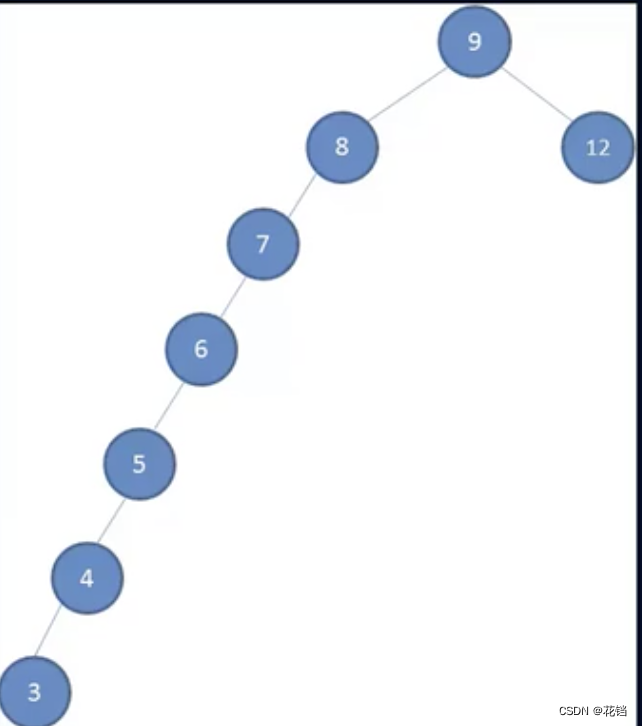
例如：有一棵初始化为 9、8、12 的二叉搜索树，然后一次插入：7、6、5、4、3、2，就形成了一棵非平衡的二叉搜索树。假设想查找 3，就需要查找 7 次才可以找到，严重降低了查找的效率。

二叉搜索树的遍历：

二叉树常见的遍历方式（此处遍历，针对所有的二叉树都适用，不仅仅是二叉搜索树）：

1. 先序遍历：以同样的方式先访问根节点，然后访问左子树，最后访问右子树。从根节点开始，以根-左-右的顺序访问。
   
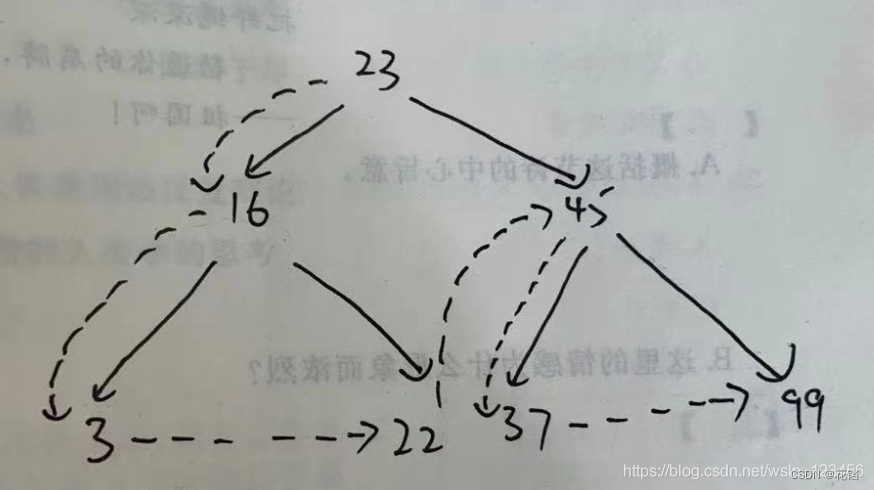
   从根节点 23 开始，可以分为 16、3、22 这棵左子树和 45、37、99 这棵右子树；
   按照根-左-右的顺序也就是先访问 23 这个根节点；
   然后访问 16、3、22 这棵左子树，此时，16 又可作为一个根节点，3 是左节点，22 是右节点，按照根-左-右的顺序也就是先访 16，然后 是3，最后是 22，此时 16、3、22 这棵左子树已经访问完毕；
   按照根-左-右的顺序接下来要访问 45、37、99 这棵右子树，此时，45 又可作为一个根节点，37 是左节点，99 是右节点，按照根-左-右的顺序也就是先访问 45，然后是 37，最后是 99。

2. 中序遍历：以同样的方式先访问左子树，然后访问根节点，最后访问右子树。从根节点开始，以左-根-右的顺序访问。

   中序遍历输出的节点的值是以升序排序的。

   
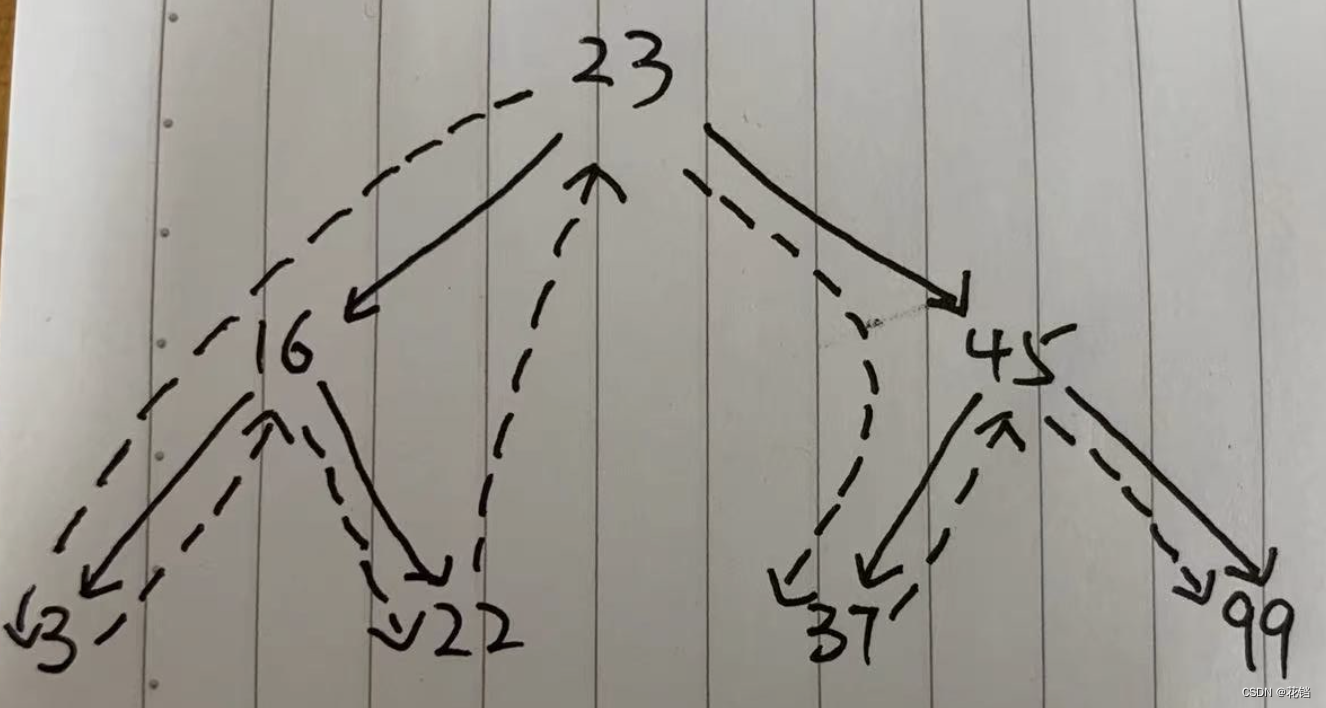
   从根节点 23 开始，可以分为1 6、3、22 这棵左子树和 45、37、99 这棵右子树；
   按照左-根-右的顺序也就是先访问 16、3、22 这棵左子树，此时，16 又可作为一个根节点，3 是左节点，22 是右节点，按照左-根-右的顺序也就是先访问 3，然后是 16，最后是 22，此时 16、3、22 这棵左子树已经访问完毕；
   按照左-根-右的顺序接下来要访问 23；
   然后是 45、37、99 这棵右子树，此时，45 又可作为一个根节点，37 是左节点，99 是右节点，按照左-根-右的顺序也就是先访问 37，然后是 45，最后是 99。

3. 后序遍历：以同样的方式先访问左子树，然后访问右子树，最后访问根节点。从根节点开始，以左-右-根的顺序访问。
   
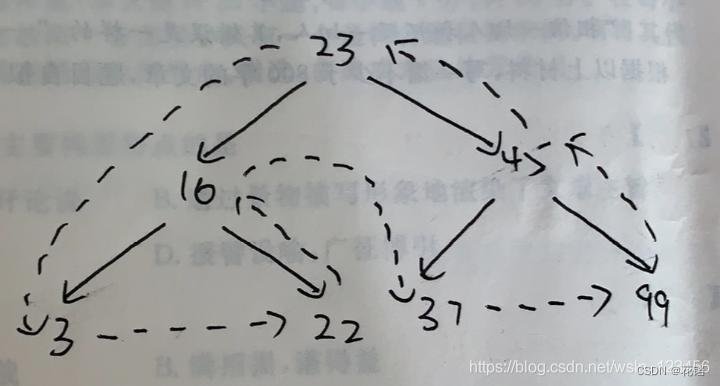
   从根节点 23 开始，可以分为 16、3、22 这棵左子树和 45、37、99 这棵右子树；
   按照左-右-根的顺序也就是先访问 16、3、22 这棵左子树，此时，16 又可作为一个根节点，3 是左节点，22 是右节点，按照左-右-根的顺序也就是先访问 3，然后是 22，最后是 16，此时 16、3、22 这棵左子树已经访问完毕；
   按照左-右-根的顺序接下来要访问 45、37、99 这棵右子树，此时，45 又可作为一个根节点，37 是左节点，99 是右节点，按照左-右-根的顺序也就是先访问 37，然后是 99，最后是 45；
   最后访问 23；

4. 还有一种层序遍历，就是一层一层地遍历，使用较少。

二叉搜索树的实现：

// 封装节点类
function Node(key) {
  // 二叉搜索树中的节点需要包含三个内容：节点本身的值、左子节点、右子节点
  this.key = key
  this.left = null
  this.right = null
}

// 封装二叉搜索树
function binarySearchTree() {
	// 二叉搜索树中的根节点
	this.root = null
}

// 二叉搜索树中的操作
// 向二叉搜索树中插入一个新的节点
binarySearchTree.prototype.insert = function(key) {
	// 1. 根据 key 创建节点
  var newNode = new Node(key)

  // 2. 判断根节点是否存在：如果不存在，直接将当前新插入的节点作为根节点
  if (this.root === null) {
    this.root = newNode
    return
  }

  // 3. 如果存在，通过递归函数插入新节点
  insertNode(this.root, newNode)
}

// 插入节点的递归函数
function insertNode(node, newNode) {
  // 1. 如果新插入节点的值小于被比较节点的值，向左查找
  if (newNode.key < node.key) {
    // 2. 如果被比较节点的值的左子节点不存在，直接将当前新插入的节点作为其左子节点
    if (node.left === null) {
      node.left = newNode
      return 
    }

    // 3. 如果被比较节点的值的左子节点存在，调用插入节点的递归函数再次比较
    insertNode(node.left, newNode)
  } else {
    // 4. 如果新插入节点的值大于被比较节点的值，向右查找

    // 5. 如果被比较节点的值的右子节点不存在，直接将当前新插入的节点作为其右子节点
    if (node.right === null) {
      node.right = newNode
      return 
    }

    // 6. 如果被比较节点的值的右子节点存在，调用插入节点的递归函数再次比较
    insertNode(node.right, newNode)
  }
}

// 测试二叉搜素树的插入
var bst = new BinarySearchTree()
bst.insert(23)
bst.insert(45)
bst.insert(16)
bst.insert(37)
bst.insert(3)
bst.insert(99)
bst.insert(22)

// 通过先序遍历的方式遍历二叉搜索树中的所有节点
BinarySearchTree.prototype.preOrderTraversal = function() {
	preOrderTraversalNode(this.root)
}

// 先序遍历的递归函数
function preOrderTraversalNode(node) {
  if (node !== null) {
    // 1. 访问经过的节点
    console.log(node.key)
    // 2. 查找经过节点的左子节点
    preOrderTraversalNode(node.left)
    // 3. 查找经过节点的右子节点
    preOrderTraversalNode(node.right)
  }
}

// 测试先序遍历
bst.preOrderTraversal() // 23 16 3 22 45 37 99

先序遍历的递归函数为什么可以按照想要的顺序输出结果呢？和函数的执行上下文有关系。

1. 23 的函数执行上下文入栈；
2. 16 的函数执行上下文入栈；
3. 3 的函数执行上下文入栈；
4. 3.left 的函数执行上下文入栈；
5. 3.left 的函数执行上下文出栈，控制权回到 3 的函数执行上下文中；

   3.left 为 null，执行完毕不再递归。

6. 3.right 的函数执行上下文入栈；
7. 3.right 的函数执行上下文出栈，控制权回到 3 的函数执行上下文中；

   3.right 为 null，执行完毕不再递归。

8. 3 的函数执行上下文出栈，控制权回到 16 的函数执行上下文中；
9. 22 的函数执行上下文入栈；
10. 22.left 的函数执行上下文入栈；
11. 22.left 的函数执行上下文出栈，控制权回到 22 的函数执行上下文中；

    22.left 为 null，执行完毕不再递归。

12. 22.right 的函数执行上下文入栈；
13. 22.right 的函数执行上下文出栈，控制权回到 22 的函数执行上下文中；

    22.right 为 null，执行完毕不再递归。

14. 22 的函数执行上下文出栈，控制权回到 16 的函数执行上下文中；
15. 16 的函数执行上下文出栈，控制权回到 23 的函数执行上下文中；
16. 45 的函数执行上下文入栈；
17. …

// 通过中序遍历的方式遍历二叉搜索树中的所有节点
BinarySearchTree.prototype.inOrderTraversal = function() {
	inOrderTraversalNode(this.root)
}

// 中序遍历的递归函数
function inOrderTraversalNode(node) {
  if (node !== null) {
    // 1. 查找经过节点的左子节点
    inOrderTraversalNode(node.left)
    // 2. 访问经过的节点
    console.log(node.key)
    // 3. 查找经过节点的右子节点
    inOrderTraversalNode(node.right)
  }
}

// 测试中序遍历
bst.inOrderTraversal() // 3 16 22 23 37 45 99

// 通过后序遍历的方式遍历二叉搜索树中的所有节点
BinarySearchTree.prototype.postOrderTraversal = function() {
	postOrderTraversalNode(this.root)
}

// 后序遍历的递归函数
function postOrderTraversalNode(node) {
  if (node !== null) {
    // 1. 查找经过节点的左子节点
    postOrderTraversalNode(node.left)
    // 2. 查找经过节点的右子节点
    postOrderTraversalNode(node.right)
    // 3. 访问经过的节点
    console.log(node.key)
  }
}

// 测试后序遍历
bst.postOrderTraversal() // 3 22 16 37 99 45 23

// 返回二叉搜索树中值最大的节点
BinarySearchTree.prototype.max = function() {
	// 1. 获取根节点
  var node = this.root

  // 2. 依次向右不断地查找，直到节点的右子节点为 null 
  // 最右边的节点就是值最大的节点
  while (node.right !== null) {
    node = node.right
  }

  return node.key
}

// 返回二叉搜索树中值最小的节点
BinarySearchTree.prototype.min = function() {
	// 1. 获取根节点
  var node = this.root

  // 2. 依次向左不断地查找，直到节点的左子节点为 null 
  // 最左边的节点就是值最大的节点
  while (node.left !== null) {
    node = node.left
  }

  return node.key
}

// 判断二叉搜索树中是否存在某个节点，如果节点存在，则返回 true；如果节点不存在，则返回 false
BinarySearchTree.prototype.search = function(key) {
	// 1. 获取根节点
  var node = this.root

  // 2. 循环搜索 key
  while(node !== null) {
    if (key < node.key) {
      node = node.left
    } else if (key > node.key) {
      node = node.right
    } else {
      return true
    }
  }

  return false
}

// 测试搜索操作
console.log(bst.search(16)) // true

二叉搜索树的删除过程：

1. 先查询要删除的节点，如果没有找到，直接返回 false；
2. 如果找到了要删除的节点：

1. 要删除的是没有子节点的节点；
2. 要删除的是只有一个子节点的节点；
3. 要删除的是有两个子节点的节点：那么需要从其子孙节点中找到一个节点，来替换当前节点。
   要找的这个节点，是子孙节点中值最接近当前节点的，要么比当前节点小一点点，要么比当前节点大一点点。
   比当前节点小一点点的节点，称为当前节点的先驱，一定是当前节点左子树中的最大值（左子树中最右侧的值）；比当前节点大一点点的节点，称为当前节点的后继，一定是当前节点右子树中的最小值（右子树中最左侧的值）。
   
   可参考上面的图来梳理删除的逻辑。

// 从二叉搜索树中删除某个节点
BinarySearchTree.prototype.remove = function(key) {
  // 1. 定义变量，存储一些信息
  var current = this.root
  var parent = null
  var isLeftChild = true

  // 2. 遍历查询要删除的节点，直到 current.key === key，跳出循环，找到要删除的节点
  while(current.key !== key) {
    parent = current

    if (key < current.key) {
      isLeftChild = true
      current = current.left
    } else {
      isLeftChild = false
      current = current.right
    }

    // 2.1. 遍历循环到最后，依然没有找到，返回 false，退出函数
    if (current === null) return false
  }

  // 3. 要删除的节点没有子节点：只需要修改其父节点的指向即可
  if (current.left === null && current.right === null) {
    if (current === this.root) {
      // 3.1. 要删除的节点是根节点
      this.root = null
    } else if (isLeftChild) {
      // 3.2. 要删除的节点是叶子节点，且是左子节点
      parent.left = null
    } else {
      // 3.3. 要删除的节点是叶子节点，且是右子节点
      parent.right = null
    }
  }
  
  // 4. 要删除的节点只有一个子节点：只需要修改其父节点的指向即可
  else if (current.right === null) {
    // 4.1 要删除的节点只有一个子节点，且只有左子节点
    if (current === this.root) {
      // 4.1.1 如果当前节点是根节点，那么让根节点指向当前节点的左子节点
      this.root = current.left
    } else if (isLeftChild) {
      // 4.1.2. 如果当前节点是其父节点的左子节点，那么让其父节点的左子节点指向当前节点的左子节点
      parent.left = current.left
    } else {
      // 4.1.3. 如果当前节点是其父节点的右子节点，那么让其父节点的右子节点指向当前节点的左子节点
      parent.right = current.left
    }
  } else if (current.left === null) {
    // 4.2. 要删除的节点只有一个子节点，且只有右子节点
    if (current === this.root) {
      // 4.2.1 如果当前节点是根节点，那么让根节点指向当前节点的右子节点
      this.root = current.right
    } else if (isLeftChild) {
      // 4.2.2. 如果当前节点是其父节点的左子节点，那么让其父节点的左子节点指向当前节点的右子节点
      parent.left = current.right
    } else {
      // 4.2.3. 如果当前节点是其父节点的右子节点，那么让其父节点的右子节点指向当前节点的右子节点
      parent.right = current.right
    }
  }

  // 5. 要删除的节点有两个子节点（代码实现以找到后继替换为例）：要修改其父节点、左子节点、右子节点的指向
  else {
    // 5.1 获取后继节点
    var succssor = getSuccssor(current)

    if (current === this.root) {
      // 5.2. 如果当前节点是根节点，那么让根节点指向后继节点
      this.root = succssor
    } if (isLeftChild) {
      // 5.3 如果当前节点是其父节点的左子节点，那么让其父节点的左子节点指向后继节点
      parent.left = succssor
    } else {
      // 5.4 如果当前节点是其父节点的右子节点，那么让其父节点的右子节点指向后继节点
      parent.right = succssor
    }

    // 5.5 后继节点是要删除节点的右子树中最左侧的节点，一定没有左子节点的，因此可以直接让后继节点的左子节点指向原先要删除节点的左子节点
    succssor.left = current.left
  }
}

// 寻找当前节点的后继的函数
function getSuccssor(delNode) {
  // 1. 定义变量，保存找到的后继
  var parent = delNode
  var current = delNode.right // 右子树中的根节点

  // 2. 循环查找右子树中的最左侧的节点
  while (current.left !== null) {
    parent = current
    current = current.left
  }

  // 修改右子节点的指向
  // 3. 判断寻找到的后继节点是否直接就是要删除节点的右子节点：如果是的话，直接提上去就可以，这棵右子树没有节点变化，不需要再做什么操作；如果不是的话，表示后继节点是要删除节点的右子节点的左子树中的某一个节点，提上去替换了要删除的节点，那么这个后继节点的指向就有问题了，后继节点一定是最左侧的节点，且不会再有左子节点，只可能会有右子节点，那么就让后继节点的父节点的 left 等于后继节点的 right，然后让后继节点的 right 等于要删除节点的 right
  if (current !== delNode.right) {
    parent.left = current.right
    current.right = delNode.right
  }

  return current
}

// 测试删除节点
bst.remove(16)
bst.postOrderTraversal() // 3 22 37 99 45 23