《算法笔记》第4章 入门篇（2）---算法初步 10.4 最短路径

原创 于 2020-09-12 12:32:01 发布 · 290 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法

这篇博客介绍了算法初步中的最短路径问题，特别是Dijkstra算法和Bellman-Ford算法。讲解了Dijkstra算法的理解、实现、应用场景，包括邻接矩阵和邻接表的比较，以及Dijkstra与DFS的结合应用。同时，讨论了Bellman-Ford算法在处理负权边时的作用，并通过实例A1003来辅助理解。最后提及了Floyd算法作为解决最短路径的另一种方法。

1.Dijkstra算法：

我的理解：

找出中介点，使原本从起点到目标点的距离能够通过中间点减少，从而超出两点之间的最短路径

引子：

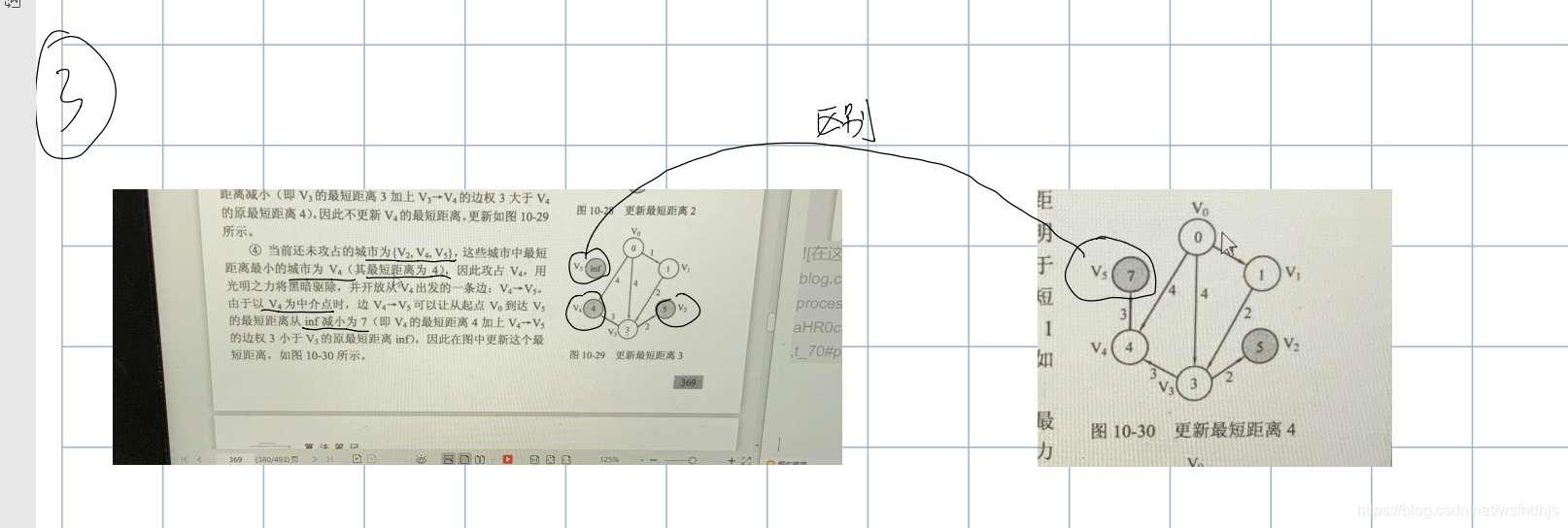
在这里插入图片描述
最短路径的方法：
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

低级斯特拉算法策略：

在这里插入图片描述
在这里插入图片描述

低级斯特拉算法的伪代码：
在这里插入图片描述

上面例子的具体实现代码：（邻接矩阵法）

#include<iostream>
using namespace std;

const int maxn=10000;
const int INF=10000000000;

int G[maxn][maxn],d[maxn],n,m,start;

bool vis[maxn]={false};

void D(int s)
{
    fill(d,d+maxn,INF);
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
        {
            return ;
        }

        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF && d[u]+G[u][v]<d[v])
                d[v]=d[u]+G[u][v];
        }
    }
}

int main()
{
    cin >> n >> m >> start;
    fill(G[0],G[0]+maxn*maxn,INF);         //初始化图G
    for(int i=0; i<m; i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        G[a][b]=c;
    }
    D(start);
    for(int i=0; i<n; i++)
        cout << d[i] << " ";
}

使用邻接矩阵和邻接表的区别：

在这里插入图片描述

邻接矩阵法：
//设置int类型 n， 邻接矩阵G, 起点到大各顶点的最小距离d 
//全局变量 MAXV为1000 INF为1000000000
/*
    void函数类型： 参数为 int类型 s
        1.使用fill函数：形参1：d  形参2:d+MAXV 形参3:INF
        2.双层for循环：知道距起点距离最短的顶点
            1.设置u为-1 MIN为INF
            2.for:如果j未被访问且距离小于最小值MIN
                1.则让u=j，且将MIn改为d[j]
    
    如果u任为-1，return则放回
    在vis中标记u已被访问过
    
    for循环：
        1.若果vis中顶点未被访问过，u可到达v 同时d[u]+G[u][v]小于d[v] 则优化d[v]
*/

const int MAXV=1000;
const int INF=10000000000;

int n,G[MAXV][MAXV],d[MAXV];
bool vis[MAXV]={false};

void D(int s)
{
    fill(d,d+MAXV,INF);
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=1000000;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
    }
    if(u==-1)
        return ;
    vis[u]=true;
    for(int v=0; v<n; v++)
    {
        if(vis[v]==false && G[u][v]!=INF && d[u]+G[u][v]<d[v])
            d[v]=d[u]+G[u][v];
    }
}
邻接表法：
//struct结构 成员：顶点v dis为边权

//vector的结构数组 Adj

//顶点数 n  最短路径数组 d  vis

const int MAXV=1000;
const int INF=1000000000000;

struct node
{
    int v;
    int dis;
};

vector<node> Adj[MAXV];

int n,d[MAXV];

bool vis[MAXV]={false};

void D(int s)
{
    fill(d,d+MAXV,INF);
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
            return ;
        vis[u]=true; 
        for(int v=0; v<Adj[u].size(); v++)
        {
            int k=Adj[u][v].v;
            if(vis[k]==false && d[u]+Adj[u][v].dis<d[k])
                d[k]=d[u]+Adj[u][k].dis;
        }
    }
}

如何将无向图改为有向图
在这里插入图片描述

最短路径求法：

在这里插入图片描述

const int maxn=1000;
const int INF=10000000000;

int G[maxn][maxn],d[maxn],pre[maxn];
bool vis[maxn]={false};


void D(int s)
{
    fill(d,d+maxn,INF);
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && MIN<d[j])
            {
                u=j;
                MIN=d[j];
            }
        }
        
        if(u==-1)
            return ;
        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF && d[u]+G[u][v]<d[v])
            {
                d[v]=d[u]+G[u][v];
                pre[v]=u;          //记录v的前驱结点为u
            }
        }
    }
}

void DFS(int s, int v)
{
    if(v==s)
    {
        cout << s << " ";
        return ;
    }
    DFS(s,pre[v]);
    cout << v << " ";
}

迪杰斯特拉算法的3种出题方式及解法：

在这里插入图片描述

新增边权：（最小花费）

在这里插入图片描述

for(int v=0; v<n; v++)
{
    if(vis[v]==false && G[u][v]!=INF)
    {
        if(d[u]+G[u][v]<d[v])
        {
            d[v]=d[u]+G[u][v];
            c[v]=c[u]+cost[u][v];
        }
        else if(d[u]+G[u][v]==d[v]) && c[u]+cost[u][v]<c[v])
            c[v]=c[u]+cost[u][v];
    }
}
新增点权：（最大物资数）

在这里插入图片描述

for(int v=0; v<n; v++)
{
    if(vis[v]==false && G[u][v]!=INF)
    {
        if(d[u]+G[u][v]<d[v])
        {
            d[v]=d[u]+G[u][v];
            w[v]=w[u]+weight[v];
        }
        else if(d[u]+G[u][v]==d[v]) && w[u]+weight[v]>w[v])
            w[v]=w[u]+weight[v];
    }
}
求最短路径条数：

在这里插入图片描述

for(int v=0; v<n; v++)
{
    if(vis[v]==false && G[u][v]!=INF)
    {
        if(d[u]+G[u][v]<d[v])
        {
            d[v]=d[u]+G[u][v];
            num[v]=num[u];      //如果u做中间结点，则在num中更新v所对应的中间元素
        }
        else if(d[u]+G[u][v]==d[v]))
            num[v]+=num[u]; //如果距离相同，则直接累加
    }
}

A1003

解题思路：

在这里插入图片描述
注意其中C1这个结点是起始的位置，C2这个结点是终点的位置
在这里插入图片描述

/*
  迪杰斯特拉算法：
  1.对于距离而言：
        都是从起点--各个点的最短路径，保存在一个数组中
  2.对于最短路径条数而言：
        从起点出发--各个点的最短路径条数，保存在一个数组中
题目只是恰好问的是c2这个点对应的最短路径条数及最大的军队数，通过迪杰斯特拉算法得到的是每一个点的

*/
#include<iostream>
#include<cstring>
using namespace std;

const int maxn=501;
const int INF=100000000000;

int d[maxn],G[maxn][maxn],num[maxn],w[maxn],weight[maxn];
bool vis[maxn]={false};

int n,m,s,must;

void D(int s)
{
    fill(d,d+maxn,INF);       //fill放的是无限大的数
    memset(num,0,sizeof(num));      //放的是确定值的数
    memset(w,0,sizeof(w));
    num[s]=1;
    d[s]=0;
    w[s]=weight[s];      //结点权值也要赋初值
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && MIN>d[j])
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
            return ;
        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF)
            {
                if(d[u]+G[u][v]<d[v])
                {
                    d[v]=d[u]+G[u][v];
                    w[v]=w[u]+weight[v];
                    num[v]=num[u];
                }
                else if(d[u]+G[u][v]==d[v])
                {
                    if(w[u]+weight[v]>w[v])
                        w[v]=w[u]+weight[v];
                    num[v]+=num[u];
                }

            }
        }
    }
}

int main()
{
    cin >> n >> m >> s >> must;
    for(int i=0; i<n; i++)        //注意n个结点放入结点权值
    {
        cin >> weight[i];
    }
    fill(G[0],G[0]+maxn*maxn,INF);
    for(int i=0; i<m; i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        G[a][b]=c;
        G[b][a]=G[a][b];
    }
    D(s);
    cout << num[must] << " " << w[must];
    return 0;
}

注意事项：

如果当程序输入完相关的信息后没有反应，注意检查for循环的次数是否和输入的次数一致

Djie+DFS

在这里插入图片描述
在这里插入图片描述

if(d[u]+G[u][v]<d[v])
{
    d[v]=d[u]+G[u][v];
    pre[v].clear();
    pre[v].push_back(u);
}

在这里插入图片描述

if(d[u]+G[u][v]==d[v])
{
    pre[v].push_back(u);
}

//设置vector的数组 pre
//void 函数 D 形参为 int类型 s
//用fill将数组d，全部初始化为INF
//在d中默认初始起点的值为0
//双层for循环，找出距离最小的结点u，和最小距离MIN
//如果u为-1，返回空
//在vis中标记u已被访问过
//for循环，如果点在vis中没访问过且从u--v存在该值
//if + else if语句： 设置前驱结点
vector<int> pre[maxn];

void D(int s)
{
    fill(d,d+maxn,INF);
    d[s]=0;        //初始位置的距离为0
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
            return ;
        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF)
            {
                if(d[u]+G[u][v]<d[v])
                {
                    d[v]=d[u]+G[u][v];
                    pre[v].clear();
                    pre[v].push_back(u);
                }
                else if(d[u]+G[u][v]==d[v])
                {
                    pre[v].push_back(u);
                }
            }
        }
    }
}

在这里插入图片描述
在这里插入图片描述

int optValue;
vector<int> path,tempPath; 
vector<int> pre[maxn];      //存放结点的先驱结点
void DFS(int v)
{
    if(v==st)
    {
        int value;
        tempPath.push_back(v);
        if(value 优于 optValue)
        {
            optValue=value;
            path=tempPath;
        }
        tempPath.pop_back();       //对于vector而言删除是pop_back
        return ;
    }
        tempPath.push_back(v);
        for(int i=0; i<pre[v].size(); i++)
        {
            DFS(pre[v][i]);        //遍历的是pre的所有先驱结点
        }
        tempPath.pop_back();   //和递归边界一样，最后都要将tempPath的最后一个结点v弹出
}

在这里插入图片描述

//边权之和
//int类型 value 初值为0
//for循环：倒着循环
//设置id=tempPath[i] idnext=tempPath[i-1]
//对value增加边id->idNext的边权

int value=0;
for(int i=tempPath.size()-1; i>0; i--)       //注意这个for循环是：从最后一个开始，倒着倒着两个两个往前走，所以根本不用到第0个位置的元素
{
    int id=tempPath[i],idnext=tempPath[i-1];
    value+=V[id][idnext];
}

















//点权之和
//int类型 value为0
//for循环：倒着循环
//int 类型 id为当前tempPath中的i
//累加

int value=0;
for(int i=tempPath.size()-1; i>=0; i--)              //这个是计算他的每一个点 
{
    int id=tempPath[i];
    value+=V[id];
}

在这里插入图片描述

A1030:

纯迪杰斯特拉算法算法

/*
    1.通过迪杰斯特拉算法算出最小路径，计算最小路径下所对应的边权，同时令数组pre记录每个结点的前驱结点，然后递归输出



*/


#include<iostream>
#include<vector>
#include<cstring>
using namespace std;

const int maxn=503;
const int INF=10000000;


bool vis[maxn]={false};

int d[maxn],c[maxn],pre[maxn];          //d的值怎么存放, pre表示先序根结点
int G[maxn][maxn],num[maxn][maxn];    //num表示的二维数组就和G表示的二维数组所代表的两个结点之间的距离一样在这里表示的是两个结点之间的路费

int n,m,s,e;

void D(int s)
{

/*
    1.找出距离起点最小的值
    2.然后将其打通，如果有能通过该结点来是原来的路径变小的，则通过该结点
*/
    fill(d,d+maxn,INF);
    memset(c,0,sizeof(c));            //注意这个c表示的数组是，从起始点到目标点的最小费用，初始化为0
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
            return ;
        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF)      //如果有合适的结点
            {
                if(d[u]+G[u][v]<d[v])        //先判断是否为最小路径，如果是，则同时修改距离d和费用c
                {
                    d[v]=d[u]+G[u][v];
                    c[v]=c[u]+num[u][v];
                    pre[v]=u;      //令结点v的前驱为u
                }
                else if(d[u]+G[u][v]==d[v] && c[v]>c[u]+num[u][v])     //如果距离相同，则就需要找出最小的费用
                {
                    c[v]=c[u]+num[u][v];
                    pre[v]=u;      //令结点v的前驱为u
                }
            }
        }
    }
}

void DFS(int v)
{
    if(v==s)         //如果是起始结点则直接输出该结点
    {
        cout << v << " ";
        return ;
    }
    DFS(pre[v]);        //递归调用v的前驱结点pre[v]
    cout << v << " ";    //输出后面的
}

int main()
{
    cin >> n >> m >> s >> e;
    fill(G[0],G[0]+maxn*maxn,INF);       //不要忘记给G进行初始化操作
    for(int i=0; i<m; i++)
    {
        int a,b,c,k;
        cin >> a >> b >> c >> k;
        G[a][b]=c;
        G[b][a]=c;
        num[a][b]=k;
        num[b][a]=k;
    }
    D(s);
    DFS(e);       //调用这个递归函数输出访问的结点，应该从最后一个结点开始
    cout << d[e] << " " << c[e];
    return 0;
}

DJ+DFS

在这里插入图片描述

/*
    DJ+DFS：DJ的作用是找到所有的最短路径，并且将所有的前驱结点放入到pre这个vector数组中，其实这个时候vector相当于一颗树，就如上图
    DFS的作用是：遍历这个树，结合第2尺标，找出使第2尺标最优的路径，为什么是深度优先搜索：答：从根结点出发，不装南墙不回头，一直到叶子结点
    同时计算第2尺标下的值

*/


#include<iostream>
#include<vector>
#include<cstring>
using namespace std;

const int maxn=503;
const int INF=10000000;

vector<int> pre[maxn],tempPath,path;
bool vis[maxn]={false};

int d[maxn],c[maxn],minconst=INF;
int G[maxn][maxn],num[maxn][maxn];

int n,m,s,e;

void D(int s)
{
    fill(d,d+maxn,INF);
    d[s]=0;
    for(int i=0; i<n; i++)
    {
        int u=-1,MIN=INF;
        for(int j=0; j<n; j++)
        {
            if(vis[j]==false && d[j]<MIN)
            {
                u=j;
                MIN=d[j];
            }
        }
        if(u==-1)
            return ;
        vis[u]=true;
        for(int v=0; v<n; v++)
        {
            if(vis[v]==false && G[u][v]!=INF)
            {
                if(d[u]+G[u][v]<d[v])
                {
                    d[v]=d[u]+G[u][v];
                    pre[v].clear();
                    pre[v].push_back(u);
                }
                else if(d[u]+G[u][v]==d[v])
                {
                    pre[v].push_back(u);
                }
            }
        }
    }
}

void DFS(int v)       //v表示当前结点
{
    if(v==s)    //如果遍历到叶子结点
    {
        tempPath.push_back(v);    //将v压入数组
        int consd=0;     
        //计算该路径上，费用
        for(int i=tempPath.size()-1; i>0; i--)
        {
            int id=tempPath[i],idnext=tempPath[i-1];
            consd+=num[id][idnext];  
        }
        if(minconst>consd)     //找出最小费用和路径
        {
            minconst=consd;
            path=tempPath;
        }
        tempPath.pop_back();
        return ;
    }
    tempPath.push_back(v);
    for(int i=0; i<pre[v].size(); i++)    //这是遍历树pre，而不是temppath，temppath只是表示临时的路径
        DFS(pre[v][i]);
    tempPath.pop_back();
}

int main()
{
    cin >> n >> m >> s >> e;
    fill(G[0],G[0]+maxn*maxn,INF);
    for(int i=0; i<m; i++)
    {
        int a,b,c,k;
        cin >> a >> b >> c >> k;
        G[a][b]=c;
        G[b][a]=c;
        num[a][b]=k;
        num[b][a]=k;
    }
    D(s);
    DFS(e);
    for(int i=path.size()-1; i>=0; i--)
            cout << path[i] << " ";
    cout << d[e] << " " << minconst;
    return 0;
}

10.4.2 Bellman-Ford算法和SPFA算法：

个人见解：BF算法也是计算最短路径（含有负值的情况），前面的三层for还是求出值为正的最短路径，后面的双层for是再去判断是否还有负的情况
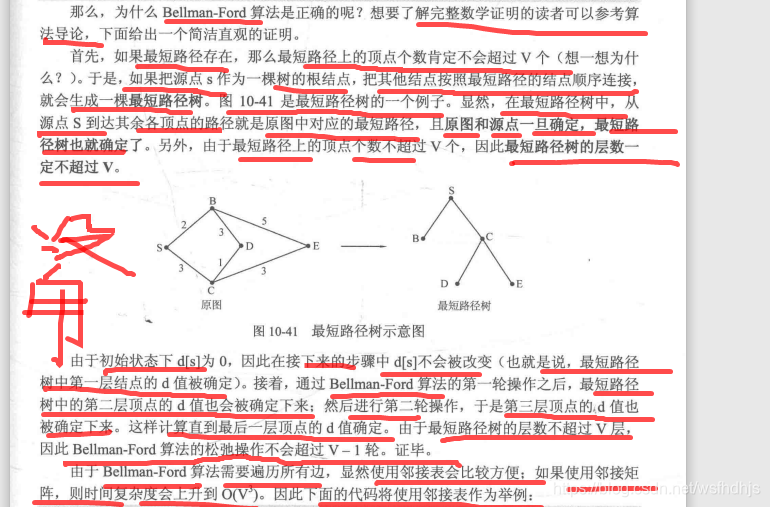
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

//设置结点结构：两个int类型值 v为邻接边的目标顶点 dis为邻接边的边权
//vector 的node数组 Adj[maxn]   //图G为邻接表
//n为最大顶点数 maxn为上限
//最短路径长度数组 d[maxn]

/*
    bool 类型 函数 Bellman 形参为 int 类型 s
    1.通过fill，将数组d的值均改为 INF
    2.设置起点的距离为0
    3.求解数组d，三层for循环：
        1.第1层for i从0--n-1，进行n-1个操作
        2.第2层for u从0--n，每轮操作遍历n条边
        3.第3层for j从0--Adj[u].size()
            1.设置int类型 v为邻接边的顶点 Adj[u][j].v
            2.设置int类型 dis为邻接边的边权 Adj[u][j].dis
            3.如果值能更小，松弛操作
            
    4.以下为判断负环的代码：
        1.对每条边进行判断for循环 u从0--n
        2.for循环：j从0--Adj[u].size() 
            1.设置int类型 v 和dis 分别放邻接点的 顶点和边权
            2.如果能松弛，则放回false
    5.最后放回true
    


*/


struct node
{
    int v;
    int dis;
};
const int maxn=10000;
vector<node> Adj[maxn];

int n;

int d[maxn];

bool Bellman(int s)
{
    fill(d,d+maxn,INF);
    d[s]=0;
    for(int i=0; i<n-1; i++)
        for(int u=0; u<n; u++)
            for(int j=0; j<Adj[u].size(); j++)
            {
                int v=Adj[u][j].v;
                int dis=Adj[u][j].dis;
                if(d[u]+dis<d[v])
                    d[v]=d[u]+dis;
            }
    //以下为判断正负环：
    for(int u=0; u<n; u++)   //对每条边进行判断
    {
        for(int j=0; j<Adj[u].size(); j++)
        {
            int v=Adj[u][j].v;
            int dis=Adj[u][j].dis;
            if(d[u]+dis<d[v]) 
                return false;       //有可达到的负环，返回false
        }
    }
    return true;  	//没有可达到的负环
}

在这里插入图片描述

通过A1003来理解BF算法：

本题其实只使用了BF算法的前半部分，由于值都是正的，所以不用后面的再次判断

//设置一个结构node ，注意在其中使用 结构数组 node(int _v, int _dis):v(_v),dis(_dis){}
//设置vector类型 node 数组 Adj[maxn]

/*
    注意使用BF算法统计最短路径的条数：
    1.设置前驱： set类型 pre[maxn]




*/

/*
    BF算法：
    1.三层for 0--n-1 0--n 0
    2.如果能松弛：
        1.更新d的距离
        2.更新点权w
        3.更新最短路径条数num
        4.统计前驱：1.在pre中清空v  2.将u插入v的下面
    3.如果距离相同：
        1.如果点权更大则更新
        2.将u插入v的后面
        3.重新统计num中的v设为0
        4.for循环，累加
*/

/*
    for循环输入信息时
    1.在Adj对应的u位置，压入N


*/

#include<iostream>
#include<vector>
#include<set>
#include<cstring>
using namespace std;

const int maxn=504;
const int INF=100000000;

struct node
{
    int v,dis;
    node(int _v, int _dis):v(_v),dis(_dis){};
};



vector<node> Adj[maxn];

int num[maxn],weight[maxn],w[maxn],d[maxn],n,m,st,e;

set<int> pre[maxn];

void Ballman(int s)
{
    fill(d,d+maxn,INF);
    memset(w,0,sizeof(w));
    memset(num,0,sizeof(num));
    num[s]=1;
    w[s]=weight[s];
    d[s]=0;
    for(int i=0; i<n-1; i++)
        for(int u=0; u<n; u++)
            for(int j=0; j<Adj[u].size(); j++)
            {
                int v=Adj[u][j].v;
                int dis=Adj[u][j].dis;
                if(d[u]+dis<d[v])
                {
                    d[v]=d[u]+dis;
                    num[v]=num[u];
                    w[v]=w[u]+weight[v];
                    pre[v].clear();
                    pre[v].insert(u);
                }
                else if(d[u]+dis==d[v])
                {
                    if(w[v]<w[u]+weight[v])
                    {
                        w[v]=w[u]+weight[v];
                    }
                    pre[v].insert(u);
                    num[v]=0;   //重新计算v的值
                    set<int>::iterator it;  //设置指针遍历set
                    for(it=pre[v].begin(); it!=pre[v].end(); it++)
                    {
                        num[v]+=num[*it];       //对num下的v进行累加
                    }
                }
            }
}

int main()
{
    cin >> n >> m >> st >> e;
    for(int i=0; i<n; i++)
        cin >> weight[i];
    for(int i=0; i<m; i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        Adj[a].push_back(node(b,c));
        Adj[b].push_back(node(a,c));
    }
    Ballman(st);
    cout << num[e] << " " << w[e];
}

在这里插入图片描述
在这里插入图片描述

/*
    设置vector的邻接矩阵Adj
    int类型：n,d[maxn],num[maxn]      num数组记录顶点的入队次数
    bool 类型： inq数组
    
    bool类型 SPFA 形参为 int 类型 s:
    
    1.初始化部分：
    将inq数组和num数组初始化为false，0
    将d数组初始化为 INF
    
    2.源点入队部分：
    设置队列Q
    将源点s如队列Q
    在inq中标记s为true
    在num中标记s对应的值++
    d中原点s的值为0
    
    3.主体部分：
        1.while循环：队列Q不为空
        2.设置int类型u的值为 队列Q的队首元素
        3.出队
        4.在inq中标记u为false
        5.for循环遍历u的所有临边
            1.记录v，dis
            2、松弛操作
                1.如果v不在队列中
                    1.将v如队
                    2.标记v为true
                    3.v的入队次数++
                    4.如果入队顶点次数大于等于n，则返回false
        6.最后返回true

*/

vector<node> Adj[maxn];

int n,d[maxn],num[maxn];

bool inq[maxn];

bool SPFA(int s)
{
    memset(inq,false,sizeof(inq));
    memset(num,0,sizeof(num));
    fill(d,d+maxn,INF);
    
    queue<int>Q;
    
    Q.push(s);
    inq[s]=true;
    num[s]++;
    d[s]=0;
    
    while(!Q.empty())
    {
        int u=Q.front();
        Q.pop();
        inq[u]=false;
        for(int j=0; j<Adj[u].size(); j++)
        {
            int v=Adj[u][j].v;
            int dis=Adj[u][j].dis;
            if(d[u]+dis<d[v])
            {
                d[v]=d[u]+dis;
                if(inq[v]==false)
                {
                    Q.push(v);
                    inq[v]=true;
                    num[v]++;
                    if(num[v]>=n)
                        return false;  //有可到达的负环
                }
            }
        }
    }
    return true;      //无可到达的负环
    
}

在这里插入图片描述

Floyd算法：

在这里插入图片描述
在这里插入图片描述

/*
    设置int类型的二维数组dis
    1.void类型 Floyd函数
        1.三层for循环：均是0--n
        2.如果从i到k，和k到j的值均不为INF，且ik+kj的值<ij的值则更新
    2.main函数
        1.对dis进行赋初值
        2.注意对主队角线上元素全部设置为0，表示自身到自身的距离为0
        3.for循环输入，以有向的方式输入，即单边输入
        4.调用Floyd函数
        5.输出值

*/

#include<iostream>
using namespace std;

const int maxn=200;

const int INF=1000000;

int dis[maxn][maxn],n,m;

void Floyd()
{
   for(int k=0; k<n; k++)
        for(int i=0; i<n; i++)
            for(int j=0; j<n; j++)
               {
                   if(dis[i][k]!=INF && dis[k][j]!=INF && dis[i][k]+dis[k][j]<dis[i][j])
                        dis[i][j]=dis[i][k]+dis[k][j];
               }
}

int main()
{
    cin >> n >> m;
    fill(dis[0],dis[0]+maxn*maxn,INF);   //注意赋初始值的方式
    for(int i=0; i<maxn; i++)
        dis[i][i]=0;
    for(int i=0; i<m; i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        dis[a][b]=c;
    }
    Floyd();
    for(int i=0; i<n; i++)
    {
        for(int j=0; j<n; j++)
        {
            cout << dis[i][j] <<  " ";
        }
        cout << endl;
    }
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值