卡特兰数

 

快速求第n位卡特兰数模板

https://blog.youkuaiyun.com/qq_36428388/article/details/77466410

https://blog.youkuaiyun.com/qq_33435265/article/details/68954205

以下内容整理自以上两篇博客

Calatan数的结论

n个“1”和n个“0”组成的2n位的二进制数，要求从左到右扫描，“1”的累计数不小于“0”的累计数，这样的二进制数的个数为著名的Calatan数 C(2n,n)/(n+1) 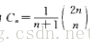，（n>=0）

证明：

令An为n个“1”和n个“0”组成的符合二进制数的个数，n个“1”和n个“0”组成的二进制数可以看作是一种类型（1型）为n个元素和另一种类型（0型）的n个元素的两种不同元素的排列，这样的排列个数位C(2n,n) = (2n)!/(n!n!)，从C(2n,n)中减去不符合要求的个数即为所求的An，考虑n个"1"和n个"0"组成的不符合要求的二进制数，不符合要求的数应为：从左到右扫描时，必然存在一个最小的k使得在这k位上首先出现"0"的累计数多于"1"的累计数，特别得，k是一个奇数，而在k之前的k-1位数中，有相等个数的"0"和"1"，而且这第k位上是"0"，现在把这前k位中每一位上的数进行交换，"1"换成"0"，"0"换成"1"，并且保持剩下的数不变，结果这样的二进制数是一个有n+1个"1"和n-1个"0"的二进制数，即一个不合要求的二进制数对应一个由n+1个"1"和n-1个"0"组成的一个排列，这个过程是可逆的：任何一个由n+1个"1"和n-1个"0"组成的2n位数，由于"1"的个数比"0"的个数多2个，2n是偶数，因此必在某个奇位数上出现"1"的累计数超过"0"的累计数，同样对他们进行交换，并使其余的不动，使之成为由n个"1"和n个"0"组成的2n位数，这时"0"的累计个数多于"1"的累计个数，是一个不符合要求的二进制数，从而不符合要求的二进制数与n+1个"1"和n-1"0"组成的排列一一对应，这样的排列个数为C(2n,n+1) = (2n)!/((n+1)!(n-1)!) 因此有An = C(2n,n)-C(2n,n+1)

 

常用应用场景：

1.如图1，从原点O（0,0）到点A（n，n）的路径数（要求中途所经过的点（a，b），满足关系式a<=b）为第n个Catalan数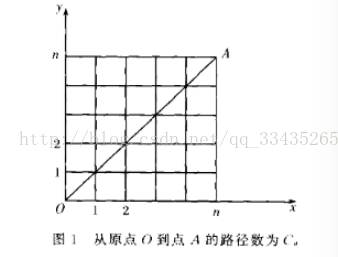

2.

3

甲、乙各n张选票的方式数(要求任一时刻所公布的甲的票数都不少于乙的票数)为Catalan数

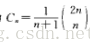
4.当然还有许多与Catalan数有关的例子，举例如下：

（1） 设有n+1个点的凸多边形，用内部不交的对角线（共n-2条）将它剖分成为n-1个三角形，不同的剖分方式数Catalan数Cn。

（2）设2n个点均匀地分布在一个圆的圆周上，能用n条不相交的弦把这些点全配成对，则这种配对的方法数是Catalan数Cn。

（3）有2n个人在售票处前站队买票，入场门票是50元，而n个人恰有这样的钱数，其他n个人每个人恰有100元钞票，不巧开始时售票处

没有零钱，如果到第一个位置为止，有50元的人数不少于有100元的人数，就称这2n个人的序列是可行的，在这种情况下，能对每个需要

找零钱的人找给零钱，这种可行的序列数为Catalan数Cn。

（4）给定不同高度的2n个人，把这些人排列成两行，每行是n个人，使得第一行的任何一个人高于第二行对应的人，这样的排列方式有Cn种。

快速求第n位卡特兰数模板

mod1e9+7版

#include <iostream>
#include <cmath>
#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <set>
#include <list>
#include <queue>
#include <stack>
#include <vector>
#include <algorithm>
#define ULL unsigned long long
using namespace std;

long long n;
const long long M=1000000007;
long long inv[1000010];
long long last,now=1;

void init()
{
    inv[1]=1;
    for(int i=2;i<=n+1;i++)inv[i]=(M-M/i)*inv[M%i]%M;
}

int main()
{
    scanf("%lld",&n);
    init();
    for(int i=2;i<=n;i++)
    {
        last=now;
        now=last*(4*i-2)%M*inv[i+1]%M;
    }
    printf("%lld\n",last);
    return 0;
}

不mod版

#include<stdio.h>
//*******************************
//打表卡特兰数
//第 n个 卡特兰数存在a[n]中，a[n][0]表示长度；
//注意数是倒着存的，个位是 a[n][1] 输出时注意倒过来。
//*********************************
int a[105][100];
void ktl()
{
    int i,j,yu,len;
    a[2][0]=1;
    a[2][1]=2;
    a[1][0]=1;
    a[1][1]=1;
    len=1;
    for(i=3;i<101;i++)
    {
        yu=0;
        for(j=1;j<=len;j++)
        {
            int t=(a[i-1][j])*(4*i-2)+yu;
            yu=t/10;
            a[i][j]=t%10;
        }
        while(yu)
        {
            a[i][++len]=yu%10;
            yu/=10;
        }
        for(j=len;j>=1;j--)
        {
            int t=a[i][j]+yu*10;
            a[i][j]=t/(i+1);
            yu = t%(i+1);
        }
        while(!a[i][len])
        {
            len--;
        }
        a[i][0]=len;
    }

}
int main()
{
    ktl();
    int T, n;
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=a[n][0];i>0;i--)
        {
            printf("%d",a[n][i]);
        }
        puts("");
    }
    return 0;
}