算法与数据结构基础

算法基础知识

算法思想

分治法

  分而治之，前端常用的一种。对一个大的问题进行求解时，将这个大问题分成相同的小问题，然后对这些小问题分别求解，这些解可以合并为该问题的解。
  前提：
1. 该问题缩小到一定的程度之后可以被很容易的解决。
2. 该问题可以被分解为若干规模较小的相同问题
3. 利用该问题分解出的子问题的解可以合并为该问题的解

动态规划

  与分治法相似，不同点在于动态规划一般用于有大量重叠子问题的情况。分治法中所有的子问题都会被重新计算一遍，而动态规划会保留子问题的解，遇上重复的就不需要计算了。用空间来换时间效率。

贪心算法

  贪心算法把眼前看到的最优解当做最优解。贪心算法不一定会得到最优解但是效率高。

数据结构（数据的组织形式）

哈希（hash）

  利用键值对进行存储。哈希可以用对象表示，也可以用数组表示。
  数组a[],a[0]=43,a[1]=12,a[2]=58.这种一一对应的关系就是键值对，一个键对应着一个值，我们需要用到值12的时候直接引用键a[1]即可。

栈

  先进后出为栈，可以用数组表示。a.push('wcy');入栈。a.pop()出栈。

队列

  先进先出为队列，也可以用数组表示。a.push('wcy');入队列。a.shift()出队列。

链表

  带有指针指向下一个元素，如果要对一串数字进行频繁的增删改操作并且不是在数据的尾部，那么用链表是一个很好的选择。因为数组里边，如果想单独删除里边的某一项，必须要把那一项删除，然后再把后边的全部往前提。
  数组查询快，链表删除快。

树

  树是层级结构，有根节点子节点以及叶子结点，没有子节点的节点称为叶子节点。
  如果一棵树没有分支，那它就是一个链表。
  对于完全二叉树和满二叉树用数组的形式存储，这样比较好取出数据，因为这两种树的节点在这棵树中的第几位可以计算出来。而其他不规则的树都用链表表示。
  二叉树：每个节点有最多两个子节点。
  满二叉树：除叶子结点外每个节点有两个子节点
  完全二叉树：在满二叉树的基础上从最后一个叶子节点开始依次往左拿掉叶子结点，不管拿掉几个剩下的二叉树都叫做完全二叉树。

排序算法

排序的可视化

冒泡排序

  第一位和第二位比较，大的往后边排。然后此时的第二位再与第三位进行比较，以此类推。每一趟都得到一个最大值，length减一。重复执行直至所有的数字都排序完毕。平均时间复杂度为O(n*n)。

js实现：

var a = [4,6,3,2,7,9,8]
var index
var length = a.length
for(;length>1; length--){
  for(index = 0; index<length-1; index++){
    a[index] > a[index+1]?(swap(index,index+1)):undefined
}
}
function swap(i,j){
  let temp = a[i]
  a[i] = a[j]
  a[j] = temp
  return a
}
console.log(a)  //[2,3,4,6,7,8,9]

选择排序

  遍历数组，找到最大值然后与数组的第一位进行交换，第二趟找到剩下的数当中的最大值，然后与此时这个数组的第二位（除去第一趟找到的那个最大值之外的第一位）进行交换，最后得到排好序的数组。

快速排序

  快速排序的的平均时间复杂度为O(m=n log2 n)，采用递归实现。设置一个mid数组，一个left数组和一个right数组，mid里边存一个数，然后拿数组里的其它数分别与它比较，小于mid[0]的push到left里边，大于mid[0]的push到right里边，然后再分别对left和right递归调用该方法，在函数里边添加判断，如果传入的数组的length小于或等于1就将其return出去，然后将三个数组连接就可以得到一个排好序的数组了。

function quickSort(a){
  if (a.length <= 1)
        return a.slice(0);
  var left = []
  var right = []
  var mid = [a[0]]
  for (let i = 1; i < a.length; i++) {
    if (mid[0] > a[i]) {
      left.push(a[i])
    } else {
      right.push(a[i])
    }
  }
  return quickSort(left).concat(mid.concat(quickSort(right)))
}
var a = [4, 3, 5, 2, 7, 9, 1, 0, 12]
console.log(quickSort(a))  // [0, 1, 2, 3, 4, 5, 7, 9, 12]

归并排序

计数排序vs桶排序vs基数排序

  计数排序必须要有一个hash作为计数的工具，无法对小数和负数进行排序。适合有确定范围的正整数，计数排序只需要遍历一遍，速度非常快，但是很耗空间。
  计数排序的时间复杂度为O(n + max)，用一个哈希来存储数组中每个元素出现的个数。哈希的长度是数组中元素的最大值，遍历需要排序的数组，数组中元素的值是我们新建的哈希表的key，数组中元素出现的次数是哈希表中对应的value。遍历完数组后将哈希表中的元素依次输出就可以得到一个排好序的数组。

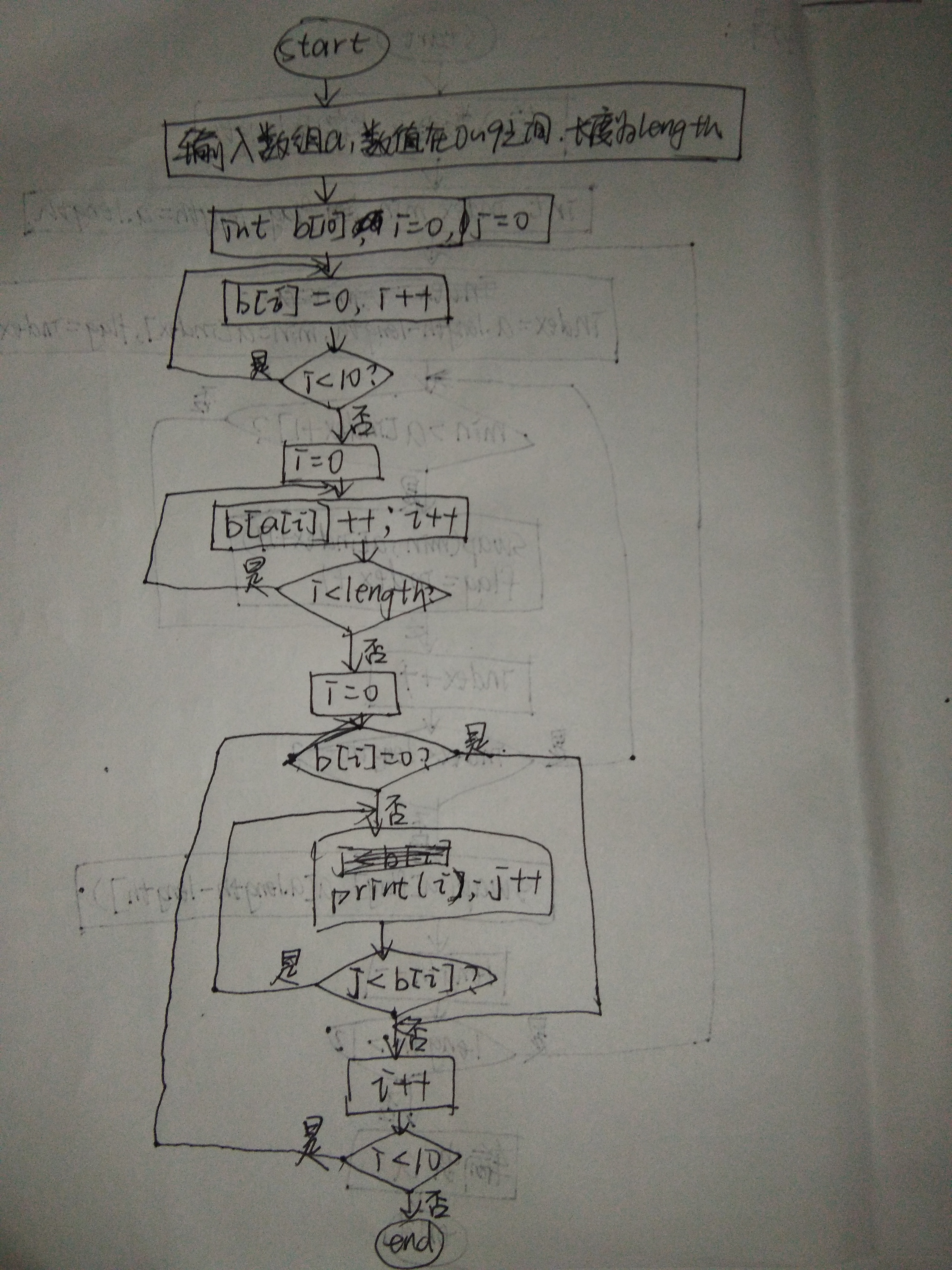
  伪代码：

int a[]={2,6,5,4,5,8,9,7};  //或者输入a的值，设置只能为正整数
int aMax = a[0];
for(int i=1; i<a.length; i++){
    if(aMax<a[i]){
        aMax = a[i];
    }
}//算出数组a的最大值aMax , aMax+1是数组b的长度
int b[aMax+1];
for(int i=0; i<a.length; i++){
    if(b[a[i]]==null){
        b[a[i]]=1;
    }else{
        b[a[i]]++;
    }//此时b中是已经排好序的数组
    //将排好序的数组输出到a中。
    int x = 0;
    for(int i=0; i<b.length; i++){
        if(b[i] != null){
            for(int j=0; j<b[i]; j++){
                a[x++] = i;
            }
        }
    }
    print(a);//将排好序的数组a输出
}

  桶排序，在桶里边放一定范围的数字，桶的个数由自己决定。计数排序是每个桶里边只放一个数字，桶的个数为待排序的数组的最大值加一（数组是从0开始的，如果你想有a[12]，那就必须要有13个桶），这种比较浪费桶（空间）。但是桶排序必须要对每个桶里的数字进行新一轮的排序。没有计数排序快。时间换空间。
  基数排序适用于大范围的特别随机的数。如果是十进制数就分为十个桶0,1,2,3,4,5,6,7,8,9，先将个位数相同的放到一个桶里，然后按队列出桶（先进先出），然后再将十位数相同的放到一个桶里，然后再出桶，依次类推直到排完最大的位数。入桶出桶操作次数多。

堆排序

堆排序的可视化
  算法描述：
1. 将一维数组视作完全二叉树，从最后一个非叶子结点开始构建最大堆，比较该结点的左子树和右子树，将大的跟该结点进行比较，如果子节点大于父节点的话将两者进行交换。
2. 如果交换过后的结点不是叶子结点，再将其视为父节点与它的左右子树进行最大堆构建。保证调整过的子树依然是最大堆。
3. 遍历一遍之后将最大堆堆顶元素与最后一个叶子结点进行交换，然后用除去最后一个结点的新的完全二叉树重新进行最大堆的构建。
4. 重复上述步骤直至只剩最后一个结点。
5. 输出排好序的数组。