机器学习笔记

其他

学术界用PyTorch。工业界PyTorch、TensorFlow都用。初学者用TensorFlow。
TensorFlow代码实现不用深究，因为我后面发论文用PyTorch。

用来学PyTorch的网站：
PyTorch官网：PyTorch 。
代码有PyTorch、TensorFlow、PADDLE、MXNET这4种实现：《动手学深度学习》 — 动手学深度学习 2.0.0 documentation 。

• 人工智能、机器学习、深度学习的区别：

人工智能（AI，Artificial Intelligence）：研究的目的是为了“模拟、延伸和扩展人的智能”。我们现在看到的貌似很高端的技术，如图像识别、NLP，其实依然没有脱离这个范围，就是“模拟人在看图方面的智能”和“模拟人在听话方面的智能”，本质上和“模拟人在计算方面的智能”没啥两样，虽然难度有高低，但目的是一样的——模拟、延伸和扩展人的智能。
机器学习（ML，Machine Learning）：常用的10大机器学习算法有：决策树、随机森林、逻辑回归、SVM、朴素贝叶斯、K最近邻算法、K均值算法、Adaboost算法、神经网络、马尔科夫。
深度学习：“深度学习”是与机器学习中的“神经网络”是强相关。深度学习又分为卷积神经网络（Convolutional neural networks，简称CNN）和深度置信网（Deep Belief Nets，简称DBN）。
总结：人工智能是一个很老的概念，机器学习是人工智能的一个子集，深度学习又是机器学习的一个子集。

• 没全看的练习：

D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week2\3.Activation Functions\C2_W2_Relu.ipynb

PyTorch学习

关于torch.flatten的笔记 - Dilthey - 博客园 https://www.cnblogs.com/dilthey/p/12376179.html

用到的url

课件PPT+Python代码：
kaieye/2022-Machine-Learning-Specialization
D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\

视频课：
【双语人译|带测试】吴恩达2022机器学习专项课程(一）自监督学习_哔哩哔哩_bilibili
San__的个人空间_哔哩哔哩_bilibili 发的3个视频课 。
用于知道自己的进度：(强推|双字)2022吴恩达机器学习Deeplearning.ai课程_哔哩哔哩_bilibili 。
接下来直接看CNN这部分，机器学习剩下部分不看了：(强推|双字)2021版吴恩达深度学习课程Deeplearning.ai。第四课01 - 1.1计算机视觉+卷积神经网络CNN_哔哩哔哩_bilibili 。

教程：
Python：Python教程 - 廖雪峰的官方网站
NumPy：NumPy 教程 | 菜鸟教程
Matplotlib：Matplotlib 教程 | 菜鸟教程
scikit-learn: machine learning in Python — scikit-learn 1.1.2 documentation https://scikit-learn.org/stable/index.html

from sklearn.linear_model import LinearRegression, SGDRegressor

怎么使用Jupyter

在菜单栏里打开 Anaconda Prompt（anaconda3）
activate tensorflow
jupyter notebook D:\Desktop\机器学习
jupyter lab D:\Desktop\机器学习

双击进入编辑模式，鼠标点击空白其他cell或者按Esc键可以进入命令模式。如果是markdown文本，需要点击运行按钮，才能显示markdown格式的文本。
Shift+Enter：运行选中的cell的代码，并且跳到下一个cell。
Ctrl+Enter：运行选中的cell的代码。

matplotlib可视化

import matplotlib.pyplot as plt
fig = plt.figure() # plt.figure(figsize=(a, b)) 生成一个空白的图片，其中figsize用来设置图形的大小，a为图形的宽， b为图形的高，单位为英寸。
fig.add_subplot(221)   #top left。表示将整个图像窗口分为2行2列，当前位置为1，第1个子图。
fig.add_subplot(222)   #top right。表示将整个图像窗口分为2行2列，当前位置为2，第2个子图。
fig.add_subplot(223)   #bottom left
fig.add_subplot(224)   #bottom right 
plt.show()

fig代表绘图窗口(Figure)；ax代表这个绘图窗口上的坐标系(axis)，一般会继续对ax进行操作。

fig, ax = plt.subplots()等价于：
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)

下方代码来自：D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week2\3.Activation Functions\C2_W2_Relu.ipynb 。

def widgvis(fig):
    fig.canvas.toolbar_visible = False
    fig.canvas.header_visible = False
    fig.canvas.footer_visible = False
def plt_act_trio():
    X = np.linspace(-5,5,100)
    fig,ax = plt.subplots(1,3, figsize=(6,2)) # 生成宽6英寸，高2英寸的空白图片，分成1行3列。
    widgvis(fig)
    ax[0].plot(X,tf.keras.activations.linear(X))
    ax[0].axvline(0, lw=0.3, c="black")
    ax[0].axhline(0, lw=0.3, c="black")
    ax[0].set_title("linear")
    ax[1].plot(X,tf.keras.activations.sigmoid(X))
    ax[1].axvline(0, lw=0.3, c="black")
    ax[1].axhline(0, lw=0.3, c="black")
    ax[1].set_title("sigmoid")
    ax[2].plot(X,tf.keras.activations.relu(X))
    ax[2].axhline(0, lw=0.3, c="black")
    ax[2].axvline(0, lw=0.3, c="black")
    ax[2].set_title("relu")
    fig.suptitle("Common Activation Functions", fontsize=14)
    fig.tight_layout(pad=0.2)
    plt.show()
plt_act_trio()

第一部分

第一周：总体介绍+一元线性回归+代价函数+梯度下降

• 监督学习：supervised learning
  • 回归：regression，预测数字 predict numbers。
    • 线性回归模型：linear regression model。
  • 分类：classification，预测类别 predict categories。
    • 分类模型：classification model。逻辑回归（分类）。
• 无监督学习：unsupervised learning
  • 聚类：clustering。
  • 异常检测：anomaly detection。
  • 降维：dimensionality reduction。

符号 notation
训练集：training set。
x：输入变量。input variable，feature。
y：输出变量。output variable，target。
m：训练例子数量。number of training examples。
（x，y）：单一的训练例子。single training example。
（x^（i），y^（i））：第i个训练例子。ith training example。

ŷ：y的估计值或预测值。estimate or the prediction for y。
f：函数function，模型 model。
f（x）=f_w，b（x）=wx+b ： 单变量线性回归 univariate linear regression，一元线性回归 linear regression with one variable。
代价函数：cost function。评价模型的一个指标，有助于我们去优化模型。
代价函数J：
下图，m是数据集中数据点的个数，也就是样本数。

截距：intercept
斜率：slope

梯度下降法：gradient descent。
局部最小值：local minima。

导数：derivative。
微积分：calculus。

同时更新w和b：simultaneously update w and b

学习率：learning rate。太小会导致梯度下降的非常慢；太大可能会导致无法到达最小值，就是梯度下降法可能不收敛，甚至可能发散。
聚集、收敛：converge。
发散：diverge。

---

第二周：Numpy（Jupyter练习中）+多元线性回归+特征缩放+多项式回归

2022-Machine-Learning-Specialization-main/Supervised Machine Learning Regression and Classification/week2/5.Week 2 practice lab Linear regression/C1_W2_Linear_Regression.ipynb：这个文件展示了所有的线性回归的公式和代码，包括f(x)、cost、gradient、gradient_desenct。

向量：vector。向量头上一般需要加上向右的箭头，当然也可以不加。
箭头：arrow。
多元线性回归 multiple linear regression。多个变量的线性回归 linear regression with multiple features。
矢量化：vectorization。

---

import numpy as np # python的科学计算包。
%matplotlib widget # matplotlib包只能绘出静态图，加上这句就能使用ipympl后端绘制动态图。注意：这一行和下方一行的先后顺序不能变，必须先%matplotlib widget，再import matplotlib.pyplot as plt，才能实现，绘出动图，且动图是在Jupyter里而不是在新键的弹窗中。
import matplotlib.pyplot as plt # python的绘图包。

a = np.array([1, 2, 3, 4])
b = np.array([-1, 4, 3, 2])
c = np.dot(a, b) # c=24。向量点乘 Vector dot product。

能在Jupyter里形成动图，且动图是在Jupyter里而不是在新键的弹窗中，的代码，的导入顺序参考：
下方代码来自：2022-Machine-Learning-Specialization-main/Supervised Machine Learning Regression and Classification/week1/4.Regression Model/C1_W1_Lab04_Cost_function_Soln.ipynb

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_uni import plt_intuition, plt_stationary, plt_update_onclick, soup_bowl
plt.style.use('./deeplearning.mplstyle')

• ndarray.shape # 数组的维度，n行m列。下面列出了几个数组的维度。

[1,2] # (2,)

[[1,2,3],
[4,5,6]] # (2,3)

[[1 2]
[3 4]
[5 6]] # (3,2)

3 # () 。标量，比如一个数字的维度是空括号。

---

• Feature scaling 特征缩放

归一化后，梯度下降能进行的更快。

normalization：标准化，归一化，规范化。
特征缩放：feature scaling。min<=x<=max，x_scaled=x/max。x_scaled在[0，1]。
平均归一化：mean normalization。min<=x<=max，x_scaled=（x-μ）/（max-min）。x_scaled在[-1，1]。
Z-score归一化：Z-score normalization。min<=x<=max，x_scaled=（x-μ）/σ。x_scaled在[-3，3]。

哪种情况需要重新归一化，哪种情况不需要，如下图。

---

一些关于特征缩放的自己的理解

包含特征缩放的线性回归的步骤：y=w₁x₁+w₂x₂²+w₃x₃³+b。对X矩阵（所有训练数据的x，不包括y）（对X矩阵一列一列进行特征缩放）进行特征缩放——>用特征缩放后的X矩阵和原始的y向量得到w_norm、b_norm——>对要预测的x数据进行相同的特征缩放——>使用w_norm、b_norm、特征缩放后的x得到预测出的y——>[可选步骤：画图时，可以画原始单位的X和预测出的y，容易别人理解图]。

问：为什么特征缩放后再进行线性回归，会得到没有特征缩放后的线性回归的，最终的预测结果y？
答：从横轴x₁或x₂或x₃，纵轴y的图的形式来考虑，一堆要用于训练的数据在图上就是一堆散点。而训练，就是找出一个函数y=w₁x₁+w₂x₂²+w₃x₃³+b，来得到w₁、w₂、w₃、b。
那么，特征缩放，即只把这些训练数据的x₁、x₂、x₃都换个单位（不改y的单位），这并不会影响这些点的散布趋势（纵轴相对横轴。图：y相对x₁。图：y相对x₂。图：y相对x₃。）。
所以，该拟合一次函数的还是会拟合一次函数，该拟合二次函数的还是会拟合二次函数。只不过用特征缩放后的训练数据得到的w₁、w₂、w₃、b是与使用未经特征缩放的训练数据得到的这些不同。

问：y=w₁x₁+w₂x₂+b。为什么特征缩放是x₁除以x₁里的一个最大值、x₂除以x₂里的一个最大值，而不是除以一个共同的值？
答：x₁都除以同一个值，x₂都除以同一个值，相当于x₁换单位，x₂换单位。x₁相对y的散点图，点的散布趋势没变。x₂相对y的散点图，点的散布趋势没变。所以没有问题。
(也可以把X和y都除以一个共同值如1000，匹配出w和b后，y=wx+b，把预测出的y再乘以1000。见C1_W2_Linear_Regression.ipynb 最下面。)

问：X矩阵有多列(y=w₁x₁+w₂x₂+b)，那么能只对一列x进行 特征缩放/同时除以某个数 吗？这样能得到正确的预测结果吗?
答：能。能。

问：X矩阵只有一列时会进行特征缩放吗，即一次函数y=wx+b，需要进行特征缩放吗？
答：不知道。盲猜下，只有一列，那没必要进行特征缩放吧。

---

• 判断梯度下降是否收敛checking gradient descent for convergence

学习曲线：learning curve。横轴是迭代次数iterations，纵轴J（$\overrightarrow{w}$，b）。一条下降的曲线。
自动收敛测试：automatic convergence test。让 ε “eplison”是0.001，当某次迭代中，J（$\overrightarrow{w}$，b）下降<=ε，就说下降收敛了。

• 如何设置学习率choose the learning rate

先用0.001作为学习率α，然后进行递归下降并画出学习曲线。然后用这个数的3倍0.003进行递归下降并画出学习曲线。再用这个数的3倍0.01，即学习率依次乘3直到学习率达到1。直到找到某个学习率的学习曲线不是平滑下降，而是有所上涨，那么就选择前面某一个不会导致上涨的学习率。即选择那个能够收敛的又能下降最快或较快的学习率。

• feature engineering 特征工程

Feature engineering：Using intuition to design new features ，by transforming or combining original features.

特征工程：通过转换或组合原始特征，使用直觉设计新特征。比如：给出了土地的长和宽，要预测土地的价格，你可以把土地的面积（面积=长×宽）作为新特征。

• polynomial regression 多项式回归

有一些关于多项式方程（一次多项式、二次多项式、三次多项式、平方根多项式。。。）的图片：以一元及二元函数为例，通过多项式的函数图像观察其拟合性能；以及对用多项式作目标函数进行机器学习时的一些理解。 - it610.com

• 一个开源的、商业上可用的机器学习工具包 Scikit-Learn：scikit-learn: machine learning in Python — scikit-learn 1.1.2 documentation

第三周：逻辑回归（分类）+过拟合+正则化（过拟合解决方法）

2022-Machine-Learning-Specialization-main/Supervised Machine Learning Regression and Classification/week3/9.Week 3 practice lab logistic regression/C1_W3_Logistic_Regression.ipynb：这个文件展示了逻辑回归的所有公式和代码（f(x)、cost、gradient、gradient_desenct、regularization的cost和gradient）。包括怎么做出非线性的决策边界。

• motivation 动机

逻辑回归：logistic regression。
类：class。==类别：category
正样本：1，true，yes，positive class，presence。
负样本：0，false，no，negative class，absence。
决策边界：decision boundary。

线性回归不足以进行逻辑回归，线性模型不足以对分类数据建模。

• logistic regression 逻辑回归

Sigmoid function，logistic function。g(z)=1/(1+e^-z)。Sigmoid函数如下图，当z趋于较大的负值时，Sigmoid函数趋于0，当z趋于较大的正值时，Sigmoid函数趋于1。

逻辑回归算法：logistic regression algorithm。


上图的公式理解为，在给定$\overrightarrow{x}$ ($\vec{x}$)、参数w、b的情况下，y=1的概率。

• decision boundary 决策边界

阈值：threshold。

为了从逻辑回归模型得到最终的预测(𝑦=0或𝑦=1)，我们使用如下公式：
if $f_{\mathbf{w},b}(x)>=0.5$, predict $y=1$
if $f_{\mathbf{w},b}(x)<0.5$, predict $y=0$

g(z)>=0.5等同于z>=0。
g(z)<0.5等同于z<0。
$z=\mathbf{w}\cdot \mathbf{x}+b$

所以有：
if $\mathbf{w}\cdot \mathbf{x}+b>=0$, the model predicts $y=1$
if $\mathbf{w}\cdot \mathbf{x}+b<0$, the model predicts $y=0$
即：
$\mathbf{w}\cdot \mathbf{x}+b=0$ 的这条线，就是决策边界。

• cost function for logistic regression 逻辑回归中的代价函数

$$f_{w,b}(x^{(i)})=sigmoid(w{x}^{(i)}+b)$$

下方代价函数（cost function）不适合逻辑回归的公式，因为当把逻辑回归公式带入如下公式后，做出的三维图，w、b、J(w，b)，是一个有许多局部最小值的曲面，如果使用梯度下降，会使得下降被终止在某些局部最小值。我们需要一个光滑的碗状的曲面。
$$J(w,b)=\frac{1}{2m}\sum _{i=0}^{m-1}(f_{w,b}(x^{(i)})-y^{(i)}{)}^2$$

逻辑损失函数：Logistic Loss Function

损耗（loss）是衡量单个示例与目标值之间的差异，而成本（cost）是对训练集损失的度量。

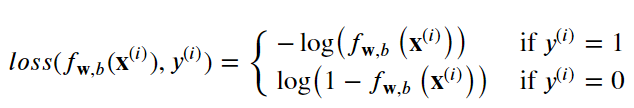
• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})$ is the model’s prediction, while $y^{(i)}$ is the target value.

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=g(\mathbf{w}\cdot {\mathbf{x}}^{(i)}+b)$ where function $g$ is the sigmoid function.

---

逻辑损失函数如下图：

---

逻辑损失函数也可以写为：
$$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=(-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)$$

• simplified cost function for logistic regression 逻辑回归的简化代价函数

logistic regression 逻辑回归（分类）：loss function 损失函数 、cost function 代价函数。

• gradient descent implementation 逻辑回归的梯度下降

逻辑回归梯度下降的公式和线性回归梯度下降的公式完全一致，只不过f(x)不同。

• the problem of overfitting 过拟合

overfitting：过拟合。模型能够非常好地拟合训练数据，但是不适用于大多数没出现在训练集中的样本。比如一个房价y-房子大小x的训练集，训练数据较少，整体呈现先快速上升，然后逐渐平稳的曲线，有个别点可能略微偏上或偏下，无法用2阶函数x²完全地拟合，但你为了能够拟合所有数据，用了一个非常高阶的函数比如x⁵，导致拟合出来的曲线能连接到所有点，但在没有点的地方会凸起或下凹，所以不适用于大多数没出现在训练集中的样本。
underfitting：欠拟合。模型不能很好地拟合训练数据。比如一个训练集，明明把点连接起来是个曲线，拟合不到线性模型上，但你非要用线性模型来拟合，导致欠拟合。
regularization：规范化，正则化。
bias：偏见。
preconception：偏见。
generalization：泛化。算法不仅能很好的拟合训练数据，也能拟合（适用于）没出现在训练集中的样本。
high-bias：高偏差。含义等同于欠拟合。
high-variance：高方差。含义等同于过拟合。

underfitting 欠拟合——overfitting 过拟合
| |
high-bias 高偏差——high-variance 高方差

• addressing overfitting 解决过拟合

解决过拟合的几种方法：
1、collect more data。获取更多训练数据。在有足够多训练数据的情况下，你用一个非常高阶的函数来拟合，也能得到很好的结果。
2、select feature，feature selection。减少特征feature的数量，只选择最能影响y的那部分特征。比如（房子大小x₁，房子年龄x₂，房子卧室数量x₃）和房子价格y，那可以只选择（房子大小x₁，房子年龄x₂）作为特征。
3、reduce size of parameters，regularization。regularization：规范化，正则化。正则化：会让你保留所有的特征，但会防止特征权重过大。特征权重过大有时会导致过拟合，而当高阶的特征的权重足够小的时候，比如w₁x⁵，w₁是一个接近0的数，那么x⁵相当于被消除了。

• cost function with regularization 带有正则化的代价函数

正则化线性回归的代价函数：

正则化逻辑回归的代价函数：

这个代价函数权衡两个目标：一个是，让第一项尽可能小，即拟合数据，即最小化（预测值-真实值）² 。另一个是，让第二项尽可能小，即让参数w_j尽可能小，减少过拟合的可能性。而λ的大小展示了你如何平衡这两个目标。
λ：lambda。希腊字母λ，是正则化参数regularization parameter。
如果λ是0，会发生过拟合，如果λ非常大，会发生欠拟合。

• regularized linear regression 线性回归的正则化

gradient descent for regularized linear regression 正则化线性回归的梯度下降：

• regularized logistic regression 逻辑回归的正则化

正则化逻辑回归的梯度下降（和正则化线性回归的梯度下降公式完全一样，只不过f(x)不同）：

第二部分：神经网络

安装tensorflow

国内镜像源：
清华：https://pypi.tuna.tsinghua.edu.cn/simple
阿里云：https://mirrors.aliyun.com/pypi/simple/
中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/
豆瓣：https://pypi.douban.com/simple/
百度: https://mirror.baidu.com/pypi/simple

都是使用activate tensorflow命令，把环境切换为tensorflow再安装。
直接在Anaconda可视化界面上安装tensorflow：安装了一天还没完成，失败。
pip install tensorflow：显示，eta（预计抵达时间（estimated time of arrival））3天，失败。
conda install tensorflow：一直停留在Solving environment: -这一步。失败。
通过conda update conda命令成功更新conda，再次使用conda install tensorflow，依然停留在Solving environment: - 这一步，失败。
conda install cudatoolkit=10 cudnn=7.6：这步貌似不需要，说tensorflow 1 是安装了这两个后才能使用GPU来运行tensorflow，tensorflow 2 不需要安装这两个，只要你有GPU，自动使用GPU来运行tensorflow。
pip install tensorflow -i https://pypi.doubanio.com/simple：后面的URL是国内镜像源，前面那几种方法都失败，就是因为是从国外下载的，速度非常慢。我用doubanio这个国内镜像源下载，3分钟就安装完成了，安装的是当前最新版本 2.6.2。

---

Jupyter中添加新的内核环境（使得Jupyter中可以使用有tensorflow包的tensorflow内核环境）

在Anaconda的tensorflow环境安装tensorflow后，可以实现PyCharm中：

# coding=utf-8
import tensorflow as tf

if __name__ == '__main__':
    print(tf.__version__) # 2.6.2
    print(tf.__file__) # E:\software-coding\anaconda3\envs\tensorflow\lib\site-packages\tensorflow\__init__.py

但是，在Jupyter中，无法切换内核环境，内核环境只能是Python 3 (ipykernel)，Jupyter中导入tensorflow会出现ModuleNotFoundError: No module named 'tensorflow'。此时，Anaconda Prompt里有：

(tensorflow) C:\Users\dell>jupyter kernelspec list # 此时，jupyter里只有1个内核环境
Available kernels:
  python3    E:\software-coding\anaconda3\share\jupyter\kernels\python3

输入以下命令：

(base) C:\Users\dell>activate tensorflow # 激活tensorflow环境
(tensorflow) C:\Users\dell>pip install -i https://pypi.tuna.tsinghua.edu.cn/simple ipykernel # 安装ipykernel，使用清华镜像
(tensorflow) C:\Users\dell>python -m ipykernel install --name tensorflow --display-name tensorflow # 将虚拟环境tensorflow导入jupyter的kernel中(自己设置显示的名字为tensorflow)
Installed kernelspec tensorflow in C:\ProgramData\jupyter\kernels\tensorflow
(tensorflow) C:\Users\dell>jupyter kernelspec list # 此时，jupyter里只有2个内核环境
Available kernels:
  python3       E:\software-coding\anaconda3\envs\tensorflow\share\jupyter\kernels\python3
  tensorflow    C:\ProgramData\jupyter\kernels\tensorflow
(tensorflow) C:\Users\dell>jupyter notebook D:\Desktop\机器学习 # 打开Jupyter notebook，此时有两个内核环境：`Python 3 (ipykernel)`、`tensorflow`，可以切换到有tensorflow的名字叫tensorflow环境。

参考链接：
Jupyter添加、删除对应虚拟环境kernel内核_jupyter_wuicer-DevPress官方社区 https://huaweicloud.youkuaiyun.com/63806aa2dacf622b8df87680.html

TensorFlow相关代码

model.fit(
    X,y,
    epochs=1000
)

model.fit()函数的参数：

• one epoch = one forward pass and one backward pass of all the training examples
• batch size = the number of training examples in one forward/backward pass. The higher the batch size, the more memory space you’ll need.
• number of iterations = number of passes, each pass using [batch size] number of examples. To be clear, one pass = one forward pass + one backward pass (we do not count the forward pass and backward pass as two different passes).
  Example: if you have 1000 training examples, and your batch size is 500, then it will take 2 iterations to complete 1 epoch.

一些常用代码：

tf.random.set_seed(1234)  # applied to achieve consistent results 用于达到一致的结果

model = Sequential(
    [ 
        Dense(1,activation="relu", name = 'l1'),
        Dense(1,activation="linear", name = 'l2')
    ]
)
model.compile(
    loss=tf.keras.losses.MeanSquaredError(),
    optimizer=tf.keras.optimizers.Adam(0.01),
)

model.fit(
    X,y,
    epochs=10
)

yhat = model.predict(X)

l1 = model.get_layer('l1')
l2 = model.get_layer('l2')
l1.get_weights()
l2.get_weights()

w1 = np.array([[-1]])
b1 = np.array([1])
l1.set_weights([w1,b1])

w2 = np.array([[1]])
b2 = np.array([0])
l2.set_weights([w2,b2])
model.fit(
    X,y,
    epochs=100
)

关于课后练习的笔记

D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week2\3.Activation Functions\C2_W2_Relu.ipynb

100条数据，X和y如下，就是拟合一条曲线，要拟合的曲线就是下图中的蓝线，是线性回归问题。

X = np.linspace(0,2*np.pi, 100)
y = np.cos(X)+1
X=X.reshape(-1,1)

w10 = np.array([[-1]])
b10 = np.array([2.6])
d10 = Dense(1, activation = "linear", input_shape = (1,), weights=[w10,b10])

w11 = np.array([[1]])
b11 = np.array([-3.7])
d11 = Dense(1, activation = "linear", input_shape = (1,), weights=[w11,b11])

yhat = relu(d10(X)) + relu(d11(X))

使用神经网络来拟合，w和b不是自己设置的，而是通过model.fit()拟合已知的X、y得到的。

model = Sequential(
    [ 
        Dense(500,activation="relu"),
        Dense(1,activation="linear")
    ]
)
model.compile(
    loss=tf.keras.losses.MeanSquaredError(),
    optimizer=tf.keras.optimizers.Adam(0.01),
)

model.fit(
    X.reshape(-1,1),y.reshape(-1,1),
    epochs=1000
)

使用上方神经网络的代码来拟合，并修改其中的参数，4种参数和4次拟合的结果，如下图。
从图2和图4可以看出，epochs数目设置太小，必然无法拟合。
而ReLU激活函数的作用就是，把z=wx+b这样的直线，通过多个unit的ReLU激活，形成分段的多条直线（就是折线图），而如果unit足够多，那么折线就足够多，就会看起来类似一条曲线。第一层使用的ReLU激活函数，所以第一层的unit个数越多，拟合效果越好，对比图1和图3也可以看出来。
目标是输入一个数字，输出一个数字，而用于训练的数据有100组。因为是输出一个数字，所以最后一层只有1个unit。

第几张图片	第一层的unit个数	model.fit()的epochs数
1	100	1000
2	100	10
3	500	1000
4	500	10

完全同样的数据、同样的神经网络、同样的参数，两次拟合出来的结果也会有不同。下图是和上图图3使用的同样的数据、神经网络、参数。应该是没有在model = Sequential()之前就，tf.random.set_seed(1234) # applied to achieve consistent results 用于达到一致的结果。

第一周：TensorFlow（神经网络概念、3种实现神经网络的代码：Tensorflow、NumPy(Forward Prop in NumPy)、Vectorized NumPy）

D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week1\9.Practice Lab Neural networks\C2_W1_Assignment.ipynb：In this exercise, you will use a neural network to recognize the hand-written digits zero and one.在这个练习中，你将使用神经网络来识别手写的数字0和1。使用了：Tensorflow Model Implementation、NumPy Model Implementation (Forward Prop in NumPy)、Vectorized NumPy Model Implementation (Optional)，并介绍了：NumPy Broadcasting Tutorial (Optional)。
3种神经网络的实现方式中，Tensorflow是最简单的一种，NumPy的两种是为了说明Tensorflow实现方式的原理。

• welcome 欢迎

neural network：神经网络。也叫做deep learning深度学习算法。
deep learning algorithm：深度学习算法。
decision trees：决策树。

• neurons and the brain 神经元和大脑

neuron：神经细胞，也叫神经元。神经细胞接受输入，进行计算，输出结果给下一个神经细胞，多个神经细胞组合成了大脑。
nucleus：细胞核。
dendrite：树突。神经细胞用于输入的突起。
axon：轴突。神经细胞用于输出的突起。
人工的神经网络从生物学上的神经细胞得到灵感，但并不是完全模仿它。

• demand prediction 需求预测

α：activation value：激活值。指一个神经元向下游的其他神经元发送的输出。在神经网络里表示，某一层向下一层发送的输出，如α，$\vec{\alpha }$（某一层有多个神经元，每个神经元都输出一个值，总共输出的多个值组合成一个向量）。
layer：层。指竖着的一层，每层可以有1个或多个神经元。input layer（layer 0）—>hidden layer（layer 1）—>output layer（layer 2）。
neural network architecture：神经网络结构。神经网络结构的问题就是：要有多少个隐藏层，每个隐藏层要有多少神经元。
perceptron：感知机。就是 一个神经元+该神经元的输入输出。$f({\sum }_{i=1}^n{w}_i{x}_i+b)=f({\vec{w}}^T\vec{x})$ 。

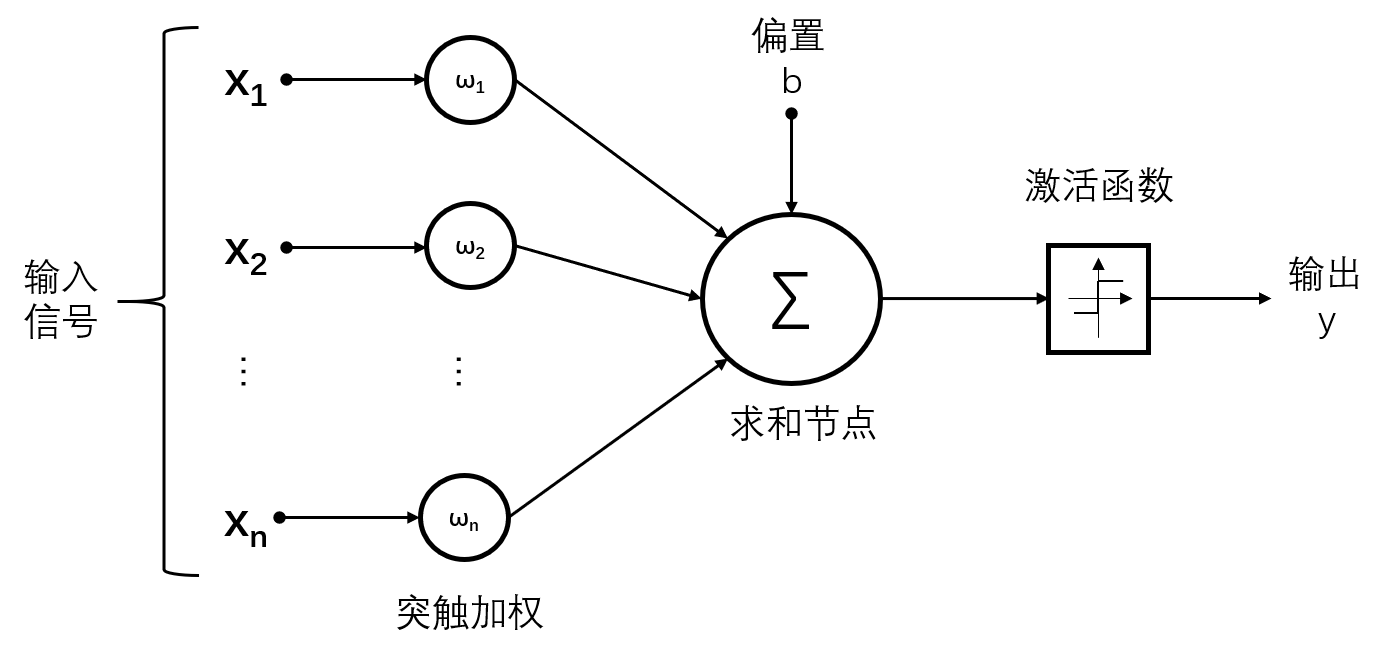
multilayer perceptron：多层感知器。有多个隐藏层的神经网络。就是神经网络的另一种叫法。
computer vision：计算机视觉。

• example：recognizing images 案例：图像识别

matrix of pixel intensity values：像素强度值矩阵。
face recognition：人脸识别。给出一张人脸照片，能输出这个照片上的人是谁。把输入的人类图像分成1000*1000的像素强度值，然后一行一行，得到一个100万像素强度值的列表。把这个列表作为输入，神经网络会分为多个隐藏层，第一个隐藏层在图像中寻找非常短的线条，第二个隐藏层寻找脸的一部分，第三个隐藏层检测这张脸与不同面部轮廓的符合程度。最后会输出这个人是谁。

• neural network layer 神经网络层

layer：层。指竖着的一层，每层可以有1个或多个神经元。给这些层从0开始往后编号，比如：input layer（layer 0）—>hidden layer（layer 1）—>output layer（layer 2）。
举例：layer 1中有3个神经元，每个神经元内都是一个逻辑回归，其中，第三个神经元的式子可以表达为：${\alpha }_3^{[1]}=g(\overrightarrow{w_3^{[1]}}\cdot \vec{x}+b_3^{[1]})$ 。式子中的上标[1]表示layer 1，下标表示是当前层的第几个神经元。而layer 1层的输出是一个向量 α [ 1 ] → = { α 1 [ 1 ] ， α 2 [ 1 ] ， α 3 [ 1 ] } \overrightarrow{α^{[1]}}=\{α^{[1]}_1，α^{[1]}_2，α^{[1]}_3\} α[1] ={α1[1]​，α2[1]​，α3[1]​} ，即组合三个神经元各自输出的标量。

• more complex neural network 更复杂的神经网络

我们说一个神经网络有4层，表示它有3个隐藏层（layer 1到layer 3）和1个输出层（layer 4）和一个输入层（layer 0），而输入层不被计入层数中，所以有4层。
对于layer 3的第二个神经元，其式子为：${\alpha }_2^{[3]}=g(\overrightarrow{w_2^{[3]}}\cdot \overrightarrow{a^{[2]}}+b_2^{[3]})$ ，式子中$\overrightarrow{a^{[2]}}$是layer 2层的输出向量，作为layer 3层的输入。
layer 0层是输入层，没有计算公式，其输出给layer 1层的是$\vec{x}$=${\alpha }^{[0]}$。
layer 4层是输出层，有计算公式，其输出的${\alpha }^{[4]}$就是最终的输出。

activation function：激活函数。上方式子${\alpha }_2^{[3]}=g(。。。)$ ，g()是sigmoid函数，在这里也可以叫做激活函数，因为g()输出了激活值α。

• 使用前向传播做预测 Inference_ making predictions (forward propagation)

handwritten digit recognition：手写数字识别。
forward propagation：前向传播。按照从左到右前进的方向进行计算，即用输入的${\alpha }^{[0]}$，计算出${\alpha }^{[1]}$，用${\alpha }^{[1]}$计算出${\alpha }^{[2]}$，依次往后，最终得到输出结果。向前传播神经元的激活值α。
backward propagation：反向传播。

• Tensorflow：inference in code 如何用代码实现推理

讲了下TensorFlow的语法。
TensorFlow：实现深度学习算法的主要框架。
Pytorch：开源的Python机器学习库，基于Torch，用于自然语言处理等应用程序。
Dense layer：another name for the layers of a neural network 神经网络层的另一个名字。有多种神经网络层，Dense layer是其中一种神经网络层。

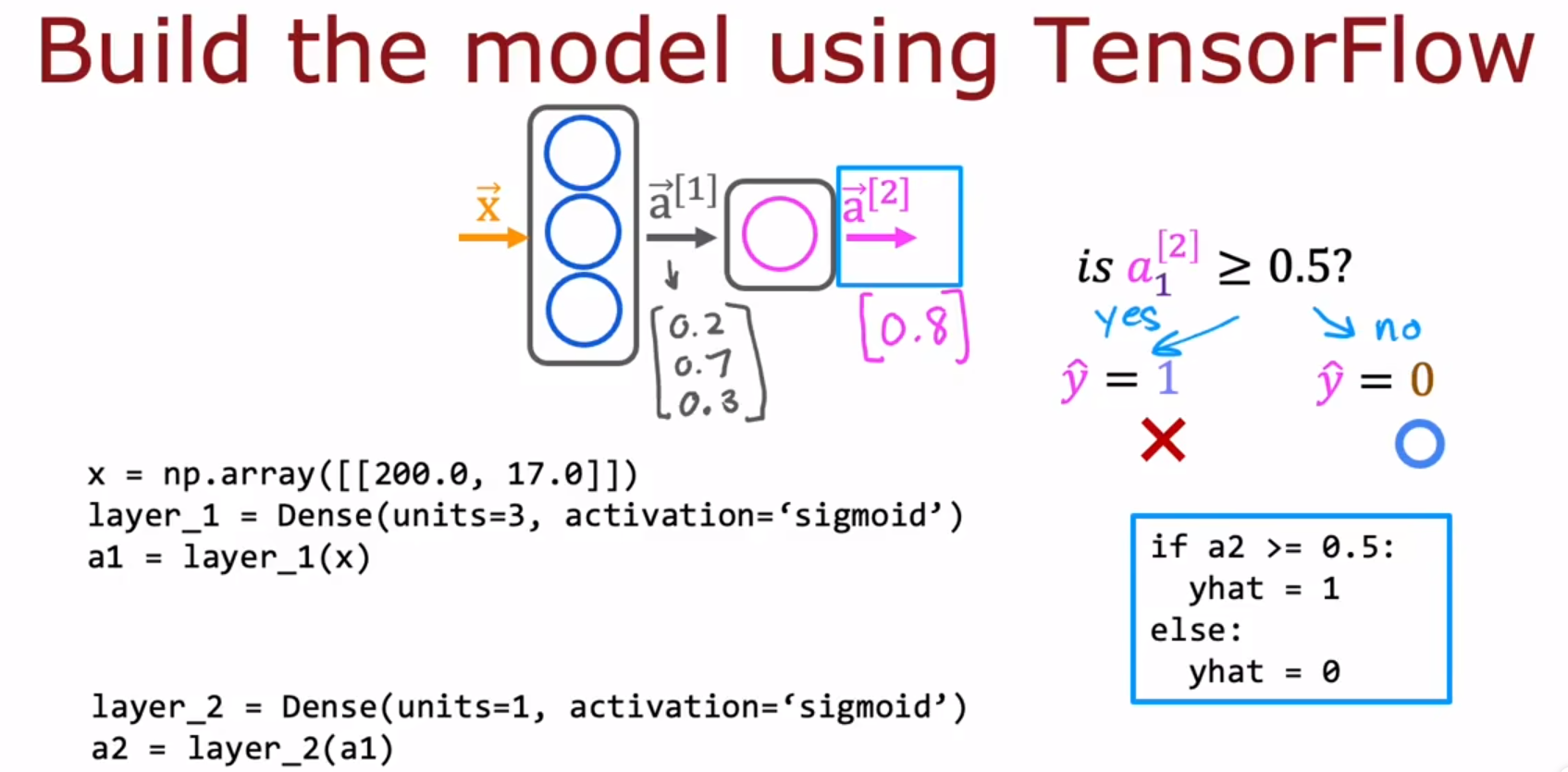
• Data in TensorFlow Tensorflow中的数据

tensor：可以理解为TensorFlow里的矩阵。
在Numpy中，np.array([1,2,3])，这只是一个没有行没有列的数组（一维），不是一个矩阵（二维）。而np.array([[1,2,3]])，这是一个1×3的矩阵。而np.array([[1],[2],[3]])，这是一个3×1的矩阵，内部的中括号会括起一行。

上图中，蓝框框起来的是代码，没框起来的是输出。layer_1是函数，这个函数接受Numpy的矩阵，然后输出一个tensor（TensorFlow里的矩阵）。这个tensor可以通过a1.numpy()来转化为Numpy中的矩阵。

• Building a neural network 构建一个神经网络

• 实践神经网络 4.1 单层中的前向传播 Forward prop in a single layer
  
  关于上图中的W1、b1、W2、b2（W1、b1是layer 1 的W和b，W2、b2是layer 2 的W和b。weights W 、 bias b）：
  W1的shape是(2,3)，b1的shape是(3)。
  W2的shape是(3,1)，b1的shape是(1)。
  原理是：The weights 𝑊 should be of size (number of features in input, number of units in the layer) while the bias 𝑏 size should match the number of units in the layer。

• 4.2 前向传播的一般实现 General implementation of forward propagation

线性代数的符号惯例（变量名规范），大写字母表示矩阵matrix，小写字母表示向量vectors和标量scalars。

• AGI猜想 5.1 是否有可能实现通用人工智能 Is there a path to AGI

AI包括AGI和ANI。
artificial general intelligence：AGI。强人工智能。能做一般人能做的所有事情的AI系统，基本没有发展。
artificial narrow intelligence：ANI。弱人工智能。自动驾驶、网络搜索等，正在高速发展。

“one learning algorithm” hypothesis：大脑皮层的听觉细胞、视觉细胞、触觉细胞，切断当前输入并换上另一种输入，可以通过听觉细胞实现看到物体，等类似操作。所以，科学家认为，大脑皮层的细胞都使用同一种算法。

• (选修)向量化计算 (optional)Vectorization 6.1 神经网络如何高效实现 How neural networks are implemented efficiently
  下图的右侧代码是左侧代码的，矩阵乘法版本的实现。
  

np.matmul()：matrix multiplication，矩阵乘法。np.array([[1]])，即使只有一个数字，但它有两个中括号，所以这是个1×1的矩阵。

This is code for a vectorized implementation of forward prop in a neural network. 这是神经网络前向传播向量化代码的实现。

def dense(A_in,W,B):
	Z=np.matmul(A_in,W)+B
	A_out=g(Z)
	return A_out

• (选修)6.2 矩阵乘法 Matrix multiplication

向量箭头：$\vec{A}$、$\overrightarrow{A}$。

vector,vector dot product：向量点积。
举例：$\vec{z}=\vec{a}\cdot \vec{w}=[1,2,3]\cdot [4,5,6]=1\times 4+2\times 5+3\times 6=4+10+18=32$

transpose：转置。
举例：
$$\vec{a}=\left[\begin{array}{c}1\\ 2\end{array}\right]$$
${\vec{a}}^T=[12]$

matrix matrix multiplication：矩阵乘法。

举例：0、1图像分类：1000张图片，每张图片有是20px × 20px，即每张图片有400个像素。

print ('The shape of X is: ' + str(X.shape)) # The shape of X is: (1000, 400)
print ('The shape of y is: ' + str(y.shape)) # The shape of y is: (1000, 1)

下方是用于model.fit()的X和y。下方的X是${\vec{A}}^T$，就是每行是一个例子，这个例子里有多个值。y也是每行是一个例子。

model.fit(
    X,y,
    epochs=1000
)

举例：
$\vec{A}$是一列一列的，${\vec{A}}^T$是一行一行的，$\vec{W}$是一列一列的。

$$\vec{A}=\left[\begin{array}{cc}1& -1\\ 2& -2\end{array}\right]$$

$${\vec{A}}^T=\left[\begin{array}{cc}1& 2\\ -1& -2\end{array}\right]$$

$$\vec{W}=\left[\begin{array}{cc}3& 5\\ 4& 6\end{array}\right]$$

$$\vec{Z}={\vec{A}}^T\vec{W}=\left[\begin{array}{cc}1\times 3+2\times 4& 1\times 5+2\times 6\\ (-1)\times 3+(-2)\times 4& (-1)\times 5+(-2)\times 6\end{array}\right]=\left[\begin{array}{cc}11& 17\\ -11& -17\end{array}\right]$$

• (选修)6.3 矩阵乘法的法则 Matrix multiplication rules

general form of how you multiply two matrices ：两个矩阵相乘的一般形式。
$\vec{Z}={\vec{A}}^T\vec{W}=$
输出矩阵$\vec{Z}$的第x行y列的数 = 第一个矩阵的第x行 点乘 第二个矩阵的第y列。
矩阵乘法有效的条件：第一个矩阵的列数 = 第二个矩阵的行数。
输出矩阵$\vec{Z}$的行数 = 第一个矩阵的行数；输出矩阵$\vec{Z}$的列数 = 第二个矩阵的列数。

• (选修)6.4 矩阵乘法代码 Matrix multiplication code

AT=A.T：A是矩阵，AT是矩阵的转置，A.T是attribute，可以理解为把A转置的方法。
Z=AT@W ：这是调用matmal函数()的另一种方法，相当于 Z=np.matmul(AT,W)。

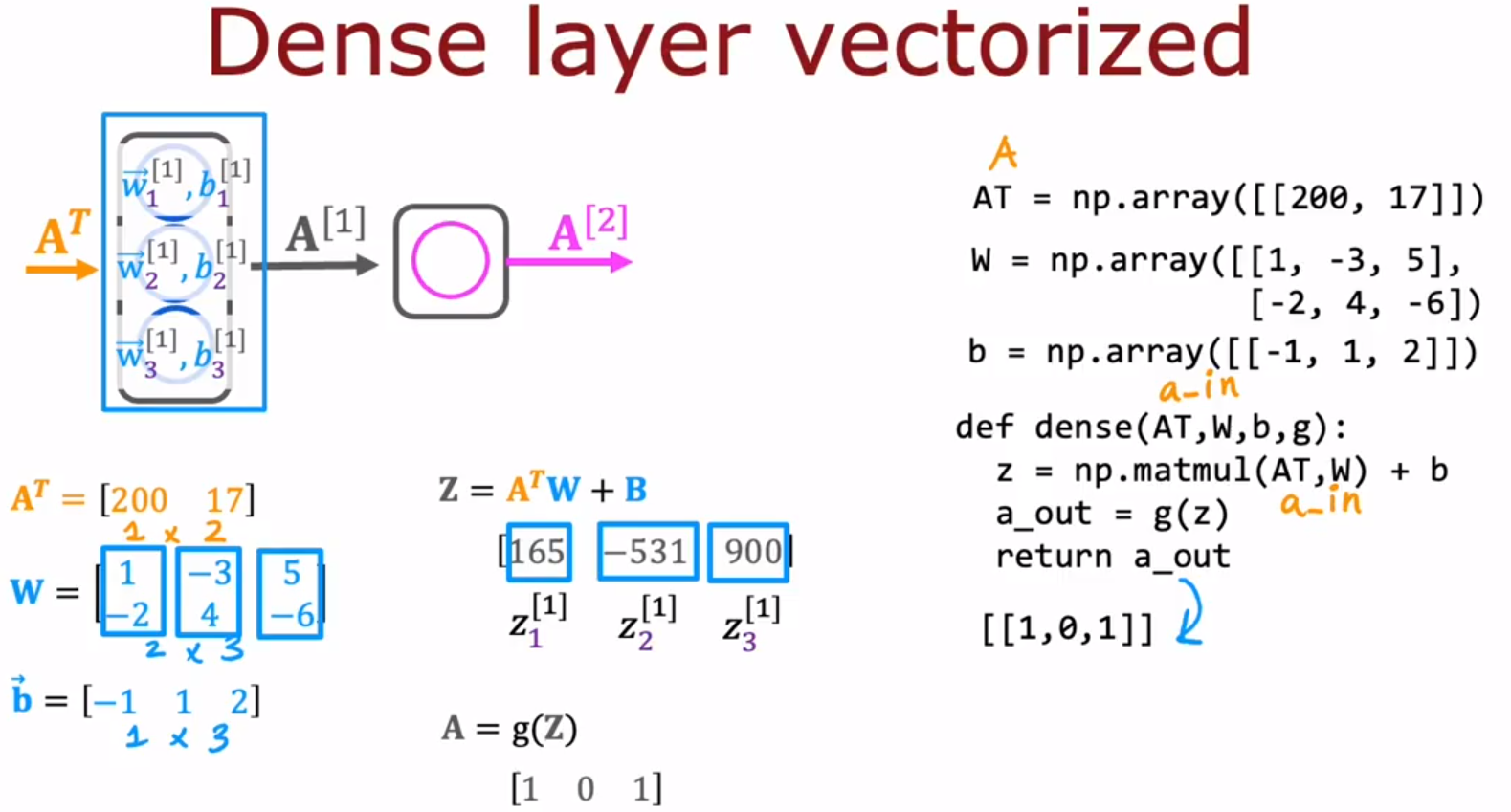
matmul matrix multiplication can be done very efficiently using fast hardware and get a huge bonus because modern computers are very good at implementing matrix multiplications such as matmul efficiently.
Matmul矩阵乘法可以使用快速硬件非常有效地完成，并获得巨大的奖励，因为现代计算机非常擅长执行矩阵乘法，例如Matmul。
意思是：神经网络的下面两种实现方式：NumPy Model Implementation (Forward Prop in NumPy)、Vectorized NumPy Model Implementation (Optional)，后者运行起来比前者快的多，花费的时间更少。

第二周：训练神经网络（神经网络的Tensorflow代码实现，如何选择激活函数：Linear、Relu、Sigmoid、Softmax，多分类，多标签分类问题，优化器Adam，卷积神经网络）

D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week2\9.Practice Lab Neural network training\C2_W2_Assignment.ipynb
：In this exercise, you will use a neural network to recognize the hand-written digits 0-9. 在这个练习中，你将使用神经网络来识别手写的数字0-9。用Tensorflow实现代码。

• TensorFlow实现 TensorFlow implementation
  
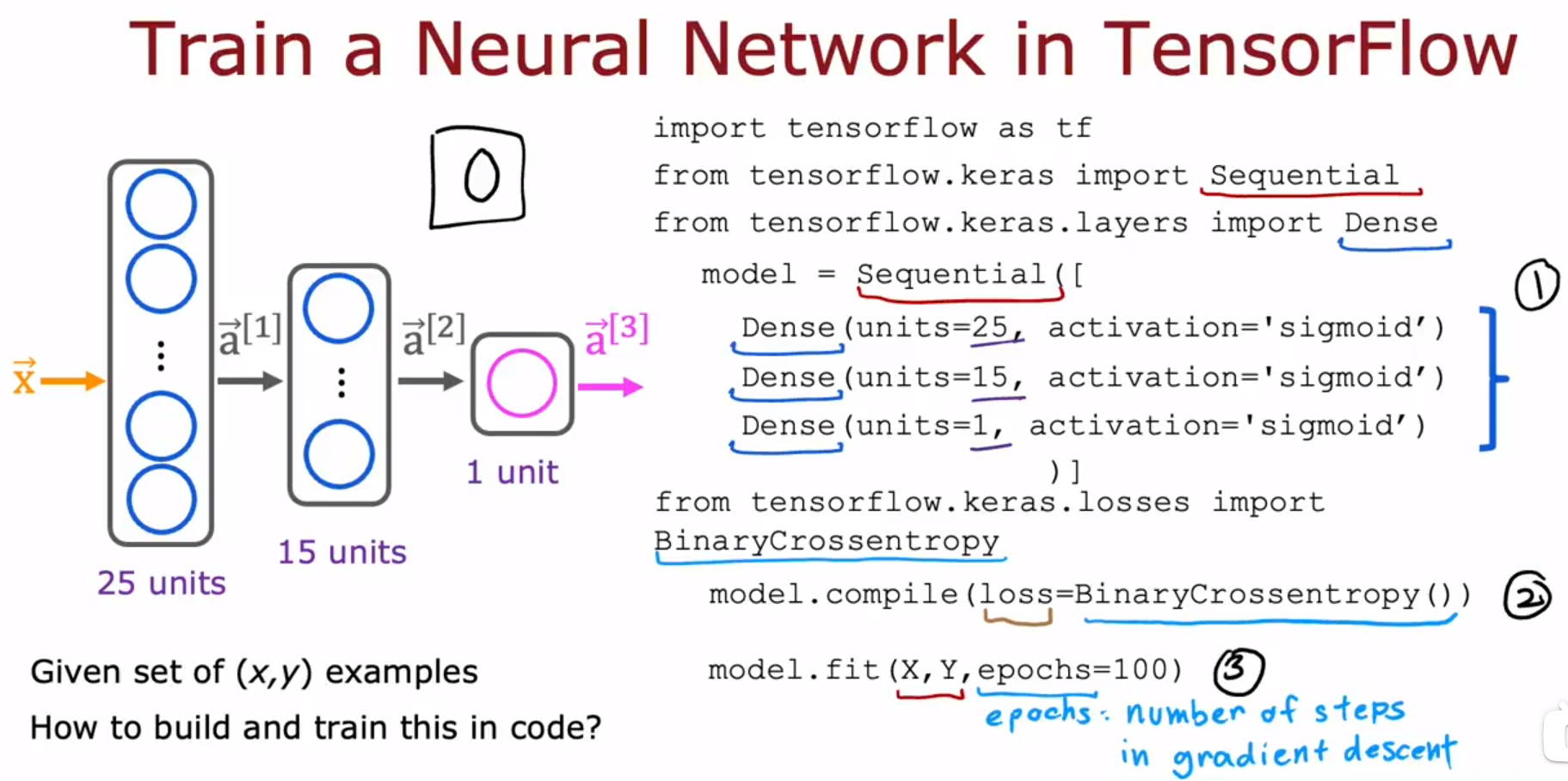
  Step 1 is to specify the model,which tells TensorFlow how to compute for the inference. Step 2 compiles the model using a specific loss function. Step 3 is to train the model.
  步骤1指定模型，该模型告诉TensorFlow如何计算推断。步骤2使用一个特定损失函数编译模型。步骤3训练模型。

• 训练细节 Training Details
  

loss=BinaryCrossentropy()，这个损失函数，就是在第一部分里讲的，logistic regression 逻辑回归（分类）：loss function 损失函数 、cost function 代价函数。，搜索标记里的内容，可以找到这个损失函数对应的公式。如下：
$$loss(f_{\mathbf{w},b}({\mathbf{x}}^{(i)}),y^{(i)})=(-y^{(i)}\log \left(f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-f_{\mathbf{w},b}\left({\mathbf{x}}^{(i)}\right)\right)$$
而已知了损失函数，就能知道代价函数：
$J(\vec{w},b)=\frac{1}{m}{\sum }_{i=1}^m[L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})]$ 。所以不需要在Tensorflow中指定代价函数是什么。

神经网络的 library库 ：TensorFlow、PyTorch。
我们只需要调用这些库就能实现神经网络。为了 tuning调参、除错debug，我们需要理解它的实现。

• Activation Functions 激活函数 8.1 sigmoid激活函数的替代方案 Alternatives to the sigmoid activation
  

• 如何选择激活函数 Choosing activation function

In choosing the activation function to use for your output layer, usually depending on what is the label y you’re trying to predict, there’ll be one fairly natural choice.
在选择用于输出层的激活函数时，通常取决于您试图预测的标签y是什么，会有一个非常自然的选择。

y的取值范围	问题类型	输出层的激活函数g(z)
0/1	Binary classification	Sigmoid
+/-	Regression	Linear activation function
0/+	Regression	ReLU（Rectified Linear Unit）

到目前为止，ReLU 激活函数 是当今许多从业者，如何训练神经网络的 最常见选择。
对比Sigmoid激活函数和ReLU激活函数，人们一般都会使用ReLU激活函数。唯一使用Sigmoid激活函数的情况是：你在处理一个二分类问题，于是你在输出层使用Sigmoid激活函数。

激活函数	函数	计算速度	model.fit(X,y,epochs=100) 梯度下降速度
ReLU	g(z)=max(0,z)	快	快
Sigmoid	$g(z)=\frac{1}{1+e^{-z}}$	慢	慢

对隐藏层的激活函数的选择，老师建议使用ReLU。

总结：
如何选择输出层的激活函数？根据y的取值范围进行选择，如下表：

y的取值范围	问题类型	输出层的激活函数g(z)
0/1	Binary classification	Sigmoid
+/-	Regression	Linear activation function
0/+	Regression	ReLU（Rectified Linear Unit）

如何选择隐藏层的激活函数？都使用ReLU激活函数。

---

也会有一些情况，选择其他的激活函数会更优。每隔几年，研究人员会提出其他的有趣的激活函数，有时它们的效果会更好一些。激活函数举例：tanh激活函数、LeakyReLU激活函数、swish激活函数。
老师认为，在大多数情况下，对于绝大多数应用，根据上方总结来选择出激活函数，就足够了。

• 为什么神经网络需要激活函数 Why do we need activation functions

一个n层的神经网络（(n-1)层是隐藏层，1层是输出层），如果它的每一层都是线性激活函数Linear activation function（函数：g(z)=z），那么输入的矩阵X经过这n层后，得到的结果f(x)是f(x)=wx+b，w和b都是一个数字，等价于线性回归模型。那么，与其使用n层的神经网络，我们不如直接使用线性回归模型。
产生这样的结果的原因是因为：一个线性函数的线性函数本身也是一个线性函数。
多层神经网络，当每一层都使用线性激活函数时，并不能提升计算复杂特征的能力，也不能学习任何比线性函数更复杂的东西。

神经网络	与同一行的神经网络相等价的模型
n层，每层都使用Linear激活函数	线性回归 linear regression
n层，n-1个隐藏层使用Linear激活函数，1个输出层使用Sigmoid激活函数	逻辑回归 logistic regression

A common rule of thumb is don’t use the linear activation function in the hidden layers of the neural network.
一个常见的经验法则是不要在神经网络的隐藏层中使用线性激活函数。
建议在神经网络的隐藏层中使用ReLU激活函数。

---

D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week2\3.Activation Functions\C2_W2_Relu.ipynb
实验报错：AttributeError: module ‘tensorflow’ has no attribute ‘layers’ 。
您使用的代码是用 Tensorflow v1.x 编写的，与 Tensorflow v2 不兼容。

• Multiclass Classification 多分类 9.1 Multiclass 多类

multiclass classification problem：target y can take on more than two possible values.
多类分类问题：目标y可以有两个以上的可能值。

• Softmax

The softmax regression algorithm is a generalization of logistic regression，which is a binary classification algorithm to the multiclass classification contexts.
softmax回归算法是逻辑回归的一种推广，它是一种针对多类分类环境的二元分类算法。

事实证明，如果应用n=2的softmax回归算法，只有2种可能的输出类，然后softmax回归的最终计算基本与逻辑回归无异。参数会有一点不同，但它最终会变成逻辑回归模型。这就是softmax回归模型是逻辑回归的推广的原因。
softmax loss、loss：

• Softmax与神经网络 Neural Network with Softmax output

• Softmax的改良代码 Improved implementation of softmax

下方两个式子在数学上是相等的，但是在计算机中计算时，由于浮点数截断，第一个式子得到的结果更加精确。

Numerical Roundoff Errors：数值舍入误差。

Better(recommended) version is actually equivalent to original implementation , at least in concept , except that is more numerically accurate.
更好的(推荐)版本实际上相当于原来的实现，至少在概念上是这样，只是在数值上更精确。

逻辑回归(分类)的多元分类的，数值舍入误差更小的，tensorflow代码如下：

逻辑回归(分类)的二元分类的，数值舍入误差更小的，tensorflow代码如下：

• 分类含多个输出 Classification with multiple outputs(Optional)

multi-label classification problem：多标签分类问题。每张图片有很多的、与之相关的标签。

• Additional Neural Network Concepts 神经网络概念加餐：Advanced Optimization 进阶优化

Adam：Adaptive Moment estimation，自适应矩估计。
Adam算法可以自动调整学习率α。
Adam算法不是全局都使用同一个学习率α，模型的每个参数都会用不同的学习率，如下图的α_{1}到α_{11}是不同的学习率。
好处：学习算法能够学习的更快。它工作通常比梯度下降快得多，它已经成为实践者训练神经网络的事实标准。

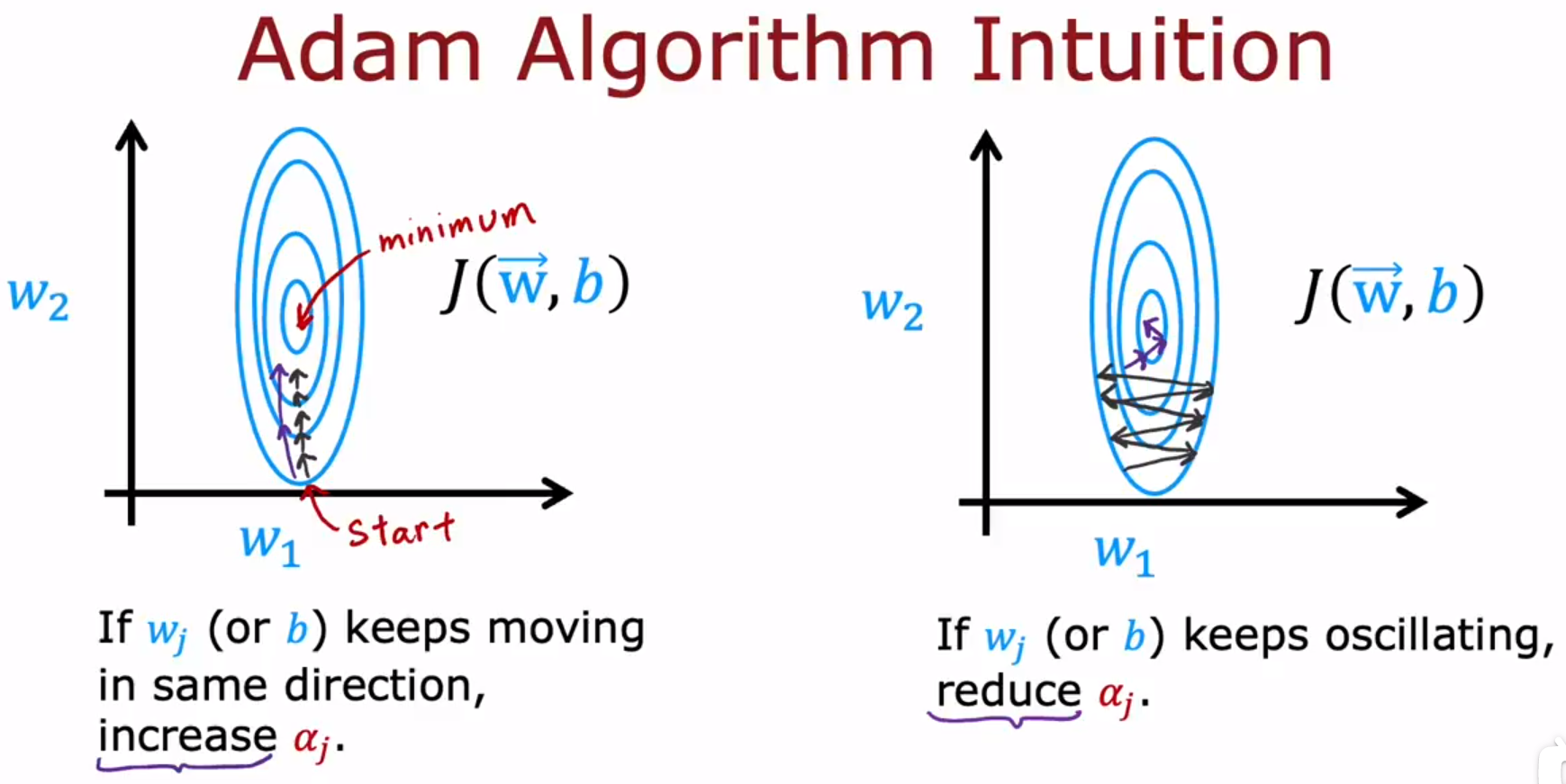
• Additional Neural Network Concepts 神经网络概念加餐：Additional Layer Types 附加层类型

Dense Layer：全连接层、稠密层。

This is the type of layer where each neuron only looks at a region of the input image is called a convolutional layer.
这种层的每个神经元只关注输入图像的一个区域，称为卷积层。
Convolutional Layer：卷积层。这一层的每个神经元，都只关注输入的一个有限的部分，不关注所有输入。
For a convolutional layer , each neuron takes as input a subset of the vector that is fed into that layer.
对于卷积层，每个神经元将输入到该层的向量的子集作为输入。

If you have multiple convolutional layers in a neural network , sometimes that’s called a convolutional neural network.
如果在神经网络中有多个卷积层，有时这被称为卷积神经网络。

It turns out that with convolutional layers you have many architecture choices , such as how big is the window of inputs that a single neuron should look at , how many neurons should layer have.
事实证明，对于卷积层，你有很多架构选择，比如单个神经元应该查看的输入窗口有多大，一层应该有多少个神经元。
And by choosing those architectural parameters effectively , you can build new versions of neural networks that can be even more effective than the dense layer for some applications.
通过有效地选择这些架构参数，你可以构建新版本的神经网络，在某些应用场景中，它甚至比全连接层更有效。

第三周：Advice for applying machine learning 机器学习实践建议（评估和选择模型，训练集、交叉验证集、测试集。诊断欠拟合还是过拟合，以及诊断出来后要怎么做【高偏差=欠拟合，高方差=过拟合】。误差分析。数据增强和数据合成。迁移学习【使用来自不同任务的数据，监督预训练和微调】。机器学习项目的全周期。倾斜数据集分类的评价指标【精确率和召回率】，及两者的权衡）

• Deciding what to try next 决定下一步要尝试什么

Machine learning diagnostic 机器学习诊断
Diagnostic：A test that you run to gain insight into what is / isn’t working with a learning algorithm , to gain guidance into improving its performance.
诊断：一种测试，您运行该测试以了解学习算法的哪些方面有效，哪些方面无效，从而获得提高其性能的指导。

Diagnostics can take time to implement but doing so can be a very good use of your time.
实施诊断可能需要时间，但这样做可以很好地利用您的时间。

• Evaluating and choosing models 评估和选择模型 ：Evaluating a model 评估模型

把数据集分成训练集training set 和测试集test set，计算test error、training error，来评估模型。

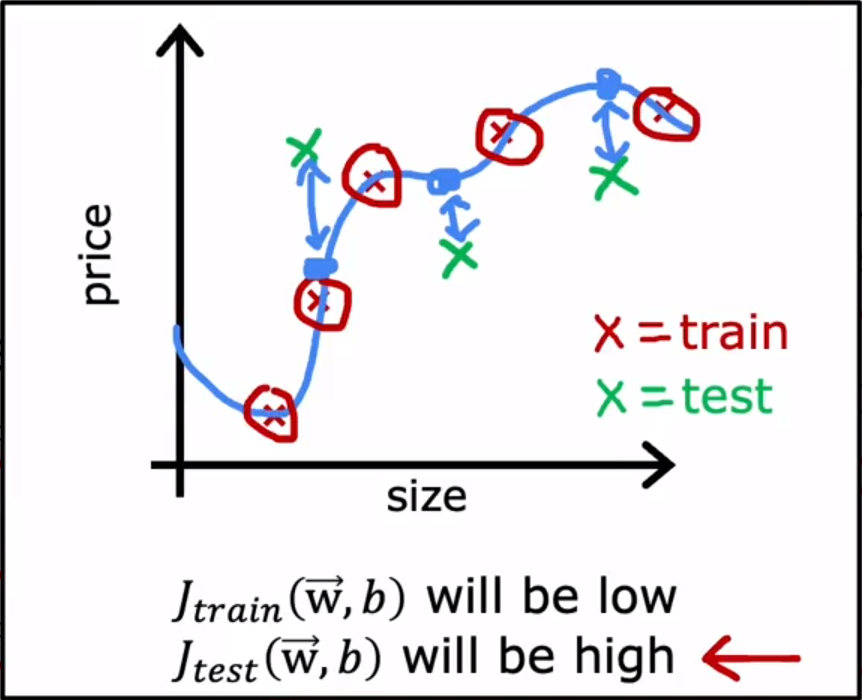
• Evaluating and choosing models 评估和选择模型 ：Model selection and training / cross validation / test sets 模型选择和 训练/交叉验证/测试集（训练集、交叉验证集、测试集）

d：the degree of polynomial 多项式次数。
下图意思是，比较不同多项式次数d的模型的 $J_{test}$ ，然后找到最小的 $J_{test}$ ，使用它对应的多项式次数d的模型。这个方法有个缺点，先使用 training set 拟合出w和b，然后使用 training set 计算 $J_{train}$ 会导致计算出的结果过于乐观，无法有效评估模型，同理，使用 test set 拟合出d，然后使用 test set 计算 $J_{test}$ ，会导致计算出的结果过于乐观，无法有效评估模型。

cv：cross-validation 交叉验证。
The name cross-validation refers to that this is an extra dataset that we’re going to use to check or trust check the validity or really the accuracy of different models.
交叉验证是一个额外的数据集，我们将使用它来检查或信任不同模型的有效性或准确性。
cross-validation set：交叉验证集。别名：validation set、development set、dev set。

正则化项 regularization term 被包含在训练对象 training objective 中，这3个公式都不包括正则化项。

下图，使用 cross-validation set 来决定选择哪个d(the degree of polynomial 多项式次数)。
下图，先使用 training set 拟合出w和b，然后使用 cross-validation set 计算 $J_{cv}$ ，比较不同多项式次数d的模型的 $J_{cv}$ ，然后找到最小的 $J_{cv}$ ，使用它对应的多项式次数d的模型，即使用 cross-validation set 拟合出d。最后使用 test set 计算 $J_{test}$， $J_{test}$ 用于 估计泛化误差 estimate generalization error。
下图举例，d=1到10的10个模型中，分别用 training set 对10个模型拟合出w和b，即$(w^{<1>},b^{<1>})$、$(w^{<2>},b^{<2>})$、。。。、$(w^{<10>},b^{<10>})$，然后，使用 cross-validation set ，对每个模型计算$J_{cv}$，即$J_{cv}(w^{<1>},b^{<1>})$、$J_{cv}(w^{<2>},b^{<2>})$、。。。、$J_{cv}(w^{<10>},b^{<10>})$，10个$J_{cv}$中，最小的是$J_{cv}(w^{<4>},b^{<4>})$，所以选择d=4对应的模型，而w和b之前已经得到了，是$(w^{<4>},b^{<4>})$。最后使用 test set 计算 $J_{test}$， $J_{test}$ 用于 估计泛化误差 estimate generalization error。因为没有使用测试集做任何决定，这确保了测试集是公平的，不会过度乐观的估计你模型的泛化能力。

下图，使用 cross-validation set 来决定选择哪个神经网络体系结构。

用处：
I use this all the time to automatically choose what model to use for a given machine learning application.
我一直使用这个来自动选择，在给定的机器学习应用场景中，应该使用什么模型。

• Bias and variance 偏差和方差：Diagnosing bias and variance 诊断偏差和方差

下图。
在某些情况下，可能会高偏差（欠拟合）和高方差（过拟合）同时存在，这种情况在线性回归中并不常见，在神经网络中比较常见。这种情况给人的直观印象是，在一部分输入上，它过拟合，在另一部分输入上，它欠拟合。

High bias (underfit) means is not even doing well on the training set , and high variance (overfit) means , it does much worse on the cross validation set than the training set.
高偏差（欠拟合）意味着算法在训练集上表现不佳，高方差（过拟合）意味着，算法在交叉验证集上的表现比训练集上的差得多。

反过来也成立，算法在训练集上表现不佳（算法在训练集上的表现比表现基准线差的多），意味着高偏差（欠拟合），算法在交叉验证集上的表现比训练集上的差得多，意味着高方差（过拟合）。
如果算法在训练集上的表现比表现基准线差的多，并且，算法在交叉验证集上的表现比训练集上的差得多，意味着该算法，既高偏差（欠拟合）又高方差（过拟合）。

• Bias and variance 偏差和方差：Regularization and bias / variance 正则化和偏差/方差

λ：the value of lambda is the regularization parameter that controls how much you trade-off keeping the parameters w small versus fitting the training data well. lambda的值是正则化参数，它控制两个目的之间的权衡程度：维持参数w小、很好地拟合 train data 训练数据。λ太小会过拟合，λ太大会欠拟合。

下图，使用 cross-validation set 来决定选择哪个λ。
下图举例，λ的12个参数中，λ的数值翻倍增长，分别用 training set 对12个参数拟合出w和b，即$(w^{<1>},b^{<1>})$、$(w^{<2>},b^{<2>})$、。。。、$(w^{<12>},b^{<12>})$，然后，使用 cross-validation set ，对每个模型计算$J_{cv}$，即$J_{cv}(w^{<1>},b^{<1>})$、$J_{cv}(w^{<2>},b^{<2>})$、。。。、$J_{cv}(w^{<12>},b^{<12>})$，12个$J_{cv}$中，最小的是$J_{cv}(w^{<5>},b^{<5>})$，所以选择λ=0.08，而w和b之前已经得到了，是$(w^{<5>},b^{<5>})$。最后使用 test set 计算 $J_{test}$， $J_{test}$ 用于 估计泛化误差 estimate generalization error。

• Bias and variance 偏差和方差：Establishing a baseline level of performance 建立表现基准水平

• Bias and variance 偏差和方差：Learning curves 学习曲线

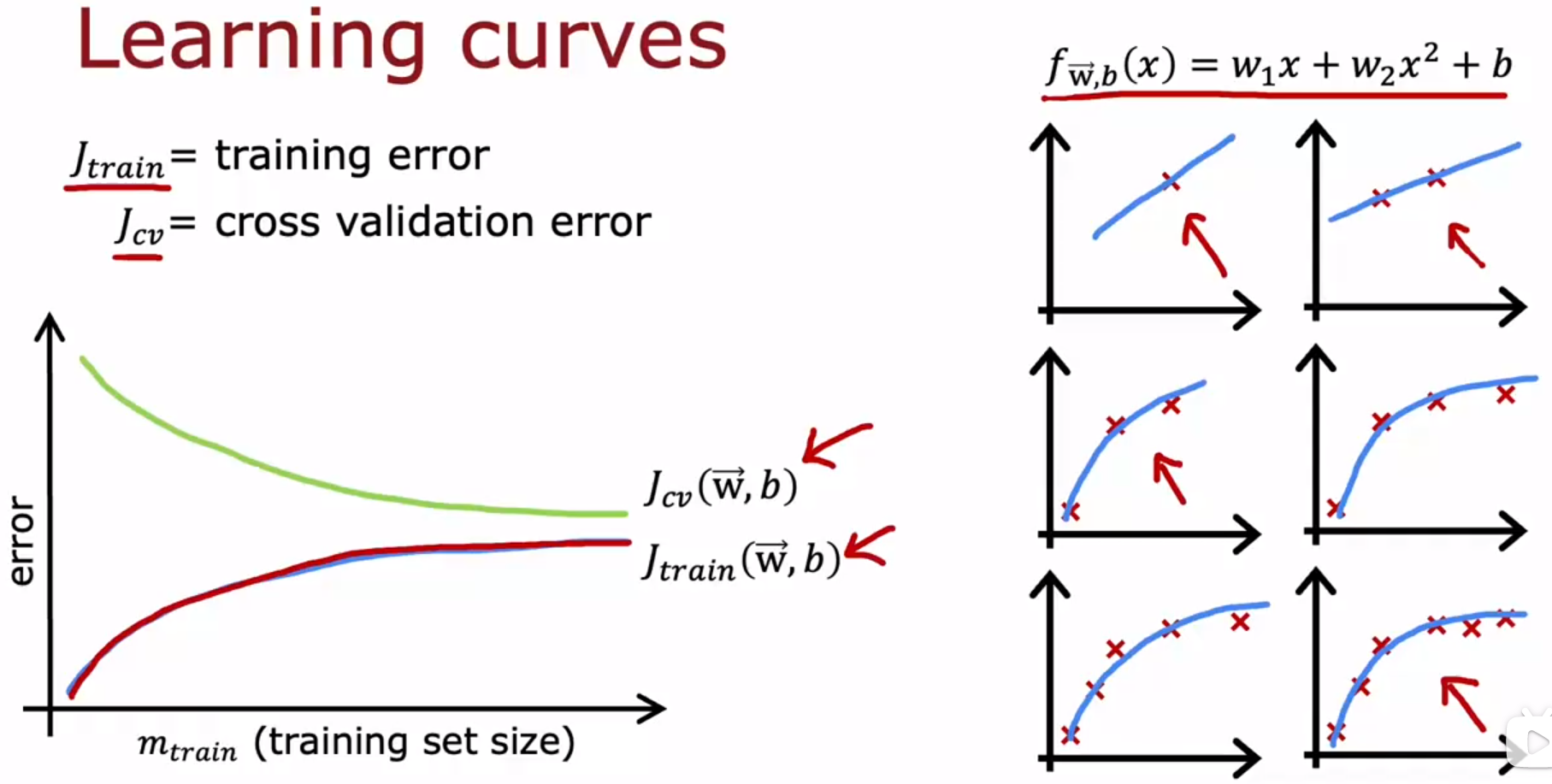
• Bias and variance 偏差和方差：Deciding what to try next revisited 决定下一步【怎么解决过拟合、欠拟合的问题】

Anyway , in case you’re wondering if you should fix high bias by reducing the training set size , that doesn’t actually help. If you reduce the training set size , you will fit the training set better , but that tends to worsen your cross-validation error and the performance of your learning algorithm , so don’t randomly throw away training examples just to try to fix a high bias problem.
无论如何，如果你想知道是否应该通过减少训练集的大小来解决高偏差（欠拟合），那实际上没有帮助。如果你减少训练集的大小，你将更好地拟合训练集，但这会让你的交叉验证误差和算法性能变差，所以不要为了解决高偏差问题而随意丢弃训练样本。

• Bias and variance 偏差和方差：Bias / variance and neural networks 偏差/方差和神经网络【在神经网络中，怎么解决过拟合、欠拟合的问题】

【在神经网络中，怎么解决过拟合、欠拟合的问题？】：欠拟合就建立更大型的神经网络，过拟合就增加训练神经网络的数据。

A large neural network will usually do as well or better than a smaller one so long as regularization is chosen appropriately.
只要选择合适的正则化参数λ，大型神经网络通常会比小型神经网络做得好或更好。

使用更大型的神经网络，只要选择合适的正则化参数λ，就不会有你想的，大型神经网络会比小型神经网络更加过拟合，这种问题。大型神经网络唯一比小型神经网络差的地方是，大型神经网络需要更好的GPU等硬件，也需要很多时间来跑。

在神经网络中，参数b通常不进行正则化，实际上，你是否正则化b没有什么区别。
不同层的正则化参数λ可以设置成不同的值。
识别手写数字分类模型的代码。

It hardly ever hurt to have a larger neural network so long as you regularize appropriately . One caveat being that having a larger new network can slow down your algorithm . So maybe that’s the one way it hurts , but it shouldn’t hurt your algorithm performance for the most part and in fact it could even help it significantly.
拥有一个更大的神经网络不会有什么坏处，只要你适当地正则化（选择正则化参数λ）。一个警告是，一个更大的新网络会减慢你的算法。这可能是它的坏处之一，但它不会在很大程度上影响算法表现，事实上，它甚至可以大大提升算法表现。

只要你的训练集不是太大，那么一种新网络，尤其是大型的神经网络，往往是低偏差机器。它可以很好地拟合非常复杂的函数。如果神经网络足够大的话，那么使用神经网络时，人不需要和偏差做斗争。

• Machine learning development process 机器学习开发过程 ：Iterative loop of ML development 机器学习开发的迭代循环

下图，左边是垃圾邮件，右边是非垃圾邮件。左边故意拼错单词：watches、Medicine、Mortgages，来骗过垃圾邮件识别器。

从字典中列出前10000个单词，每个单词作为一个特征，一封邮件有10000个特征，每个特征是：邮件中是否有这个单词（是1，否0），或者，邮件中出现几次这个单词（次数），如此得到一封邮件的特征向量 $\vec{x}$ 。

列出多种解决误差的方法，你来决定这些解决方法中哪一个更有前途，选择更有前途的方法可以加速你的项目，比你选择一些不太有前途的方向容易10倍。选择哪一个解决方法呢？举例：当有高偏差（欠拟合）时，就不使用收集更多数据的方法，当有高方差（过拟合）时，可以使用收集更多数据的方法。

• Machine learning development process 机器学习开发过程 ：Error analysis 误差分析

Pharma：pharmaceutical sales 医药销售。
误差分析举例：交叉验证集有500个邮件，其中有100个邮件被算法错误分类，人工找出这100个邮件之间的一些共同特征，列出每个特征有多少个错误分类的邮件匹配该特征，按照错误分类邮件数量对（特征，错误分类邮件数量）进行降序排序，按照从上到下的顺序来解决，即先解决最影响算法精确度的大问题。

这些特征可以同时存在，并不互相排斥，比如一封邮件，可以既有这个特征，又有那个特征，比如一封邮件，既是医药销售垃圾邮件，又有不寻常的路由。

假如被算法错误分类的邮件太多了，比如有1000个，人工看不过来，就会随机抽取一个子集来看，通常是100个或几百个，因为这是你在合理时间内能看的过来的数量。

排序后发现，最影响算法精度的问题是：医药销售邮件、钓鱼邮件。已知问题是什么，现在来解决它。
改进医药销售邮件（垃圾邮件）分类器的方法：1、增加一些特征，关于常见的推销药品名字。2、获取更多医药销售邮件来训练算法。
改进钓鱼邮件（偷密码）（垃圾邮件）分类器的方法：1、增加一个新特征，编写带有额外功能的代码，以查看邮件是否链接到可疑的URL，是1否0。2、获取更多钓鱼邮件来训练算法。

误差分类要点：手动检查一组算法错误分类或标记的样本，通常分析完以后，下一步要做什么的灵感就来了，即它可以将你的注意力集中在更重要（最影响算法分类有效性）、更有前途（解决后收益最大）的问题上。有时误差分析还可以告诉你，某种误差非常罕见，不值得你花那么多时间来修复。你不修复这种罕见的误差，可以节省时间。

再看下图，就知道哪个解决方法更有前途。这几种方法更有前途：收集更多医药销售邮件和钓鱼邮件，增加特征关于常见的推销药品，增加特征关于邮件是否链接到可以的URL。（上图，算法21%的错误分类来自医药销售邮件，算法18%的错误分类来自钓鱼邮件）。
解决邮件内的拼写错误（上图，算法3%的错误分类来自拼写错误）几乎没用，解决不寻常的邮件路由（上图，算法7%的错误分类来自不寻常的邮件路由）有效果但不多。

误差分析的局限性：它更容易处理人类擅长的问题，对于人类都不擅长的任务，可能就无法进行误差分析。比如：人可以分辨一封邮件是否是垃圾邮件，但无法预测人们会在网站上点击什么广告。

• Machine learning development process 机器学习开发过程 ：Adding data 添加数据

data augmentation 数据增强：data augmentation takes an existing training example and modifies it to create another training example. 数据增强采用现有的训练示例，并对其进行修改以创建另一个训练示例。用于OCR光学字符识别、语音识别。比如：对图片进行旋转、放大、缩小、镜面、改变对比度、增加噪声点等操作，形成新图片，对一句语音进行增加各种背景噪声，形成新音频。
OCR：Optical Character Recognition 光学字符识别。
下图，对一个字母A的图片进行 旋转、放大、缩小、改变图像对比度、镜面，得到更多关于A的图像，来作为训练集。而有了更多的A图像的训练集，可以增加算法对A的光学字符识别的精确度。

speech recognition 语音识别。
把一句话的音频，叠加各种噪音背景音，得到各种有噪音的这句话的音频，这是数据增强，用于训练算法对有噪音音频的语音识别。

要针对测试集中可能出现的情况进行数据增强，产生新的训练数据来训练算法，才能提高算法的精确度。
使用测试集中不会出现的情况进行数据增强，产生新的训练数据来训练算法，无法提高算法的精确度。
比如OCR光学字符识别，现实中人手写字母会出现扭曲，但不会出现噪声斑点，所以使用数据增强创造新的训练数据时，就只使用扭曲字母图像的数据增强方法，而不使用在字母图像上加噪声斑点的数据增强方法。

Data synthesis：数据合成。从空白开始创造全新的例子，不是通过修改现有的示例，而是通过创造全新的示例。数据合成一般被用于 computer vision toss 计算机视觉干扰，在其他应用中较少使用，对音频来说也不多。

Photo OCR / Photo Optical Character Recognition：照片OCR / 照片光学字符识别。让计算机自动读取出现在图片中的文本。

下图，左边是照片OCR中的真实数据，是在照片中出现的字母。照片OCR中的一个关键任务是，能够看到像这样的小图像，并识别出中间的字母，可以使用数据合成为这项任务创建人工数据。
右边是人工合成的数据，打开电脑的文本编辑器，写一些单词，设置不同字体、大小、颜色等，然后截图。

传统AI是 model-centric approach 以模型为中心的AI，指的是：数据集不变，研究人员专注于改进代码、算法、模型。
新型AI是 Data-centric approach 以数据为中心的AI，这建立在机器学习研究的范示上，模型（线性回归、逻辑回归、神经网络、决策树）很成熟，也能很好地用于多种应用，所以有时采用以数据为中心的方法更有效，专注于设计你的算法需要的数据。比如：使用 数据增强（data augmentation）、数据合成（Data synthesis） 的技术，创造更多数据来训练算法。比如：通过误差分析，知道缺少哪种特征的数据，然后去收集这种数据。

• Machine learning development process 机器学习开发过程 ：Transfer learning : using data from a different task 迁移学习 ：使用来自不同任务的数据

首先在与任务不太相关的大型数据集上进行训练（监督预训练），然后在与任务相关的小型数据集上进一步参数调优（微调）。

supervised pre-training：监督预训练。比如任务是手写数字0-9识别，你先在一百万张100种动物图像上训练神经网络，训练出识别100种动物的神经网络。

fine tuning：微调。指使用你已经初始化的或从预训练中获取到的参数，然后运行梯度下降，进一步微调权重，以适应你想拟合的特定应用。
比如，使用预训练得到的识别100种动物的神经网络，4个隐藏层和一个输出层，参数是w1、b1到w5、b5，因为识别100个动物和识别10个数字，类别数目不同，输出层的w、b的shape不同，所以需要舍弃掉原先的输出层和w5、b5，重新拟合输出层。
有两个选项：
选项1、4个隐藏层的w1、b1到w4、b4都固定，使用手写数字0-9的图片来微调输出层，即只训练w5、b5。选项1用于非常小的训练集。
选项2、4个隐藏层的w1、b1到w4、b4不固定，只把预训练得到的w1、b1到w4、b4的值作为起始值，使用手写数字0-9的图片，来训练所有参数，即训练w1、b1到w5、b5。选项2用于稍微大一点的训练集。

迁移学习的原理：预训练提供了一些合理的参数，然后通过将这些参数迁移到新的神经网络，新神经网络的初始值更合适了，这样我们只需要让算法再学习一点，它就能成为一个很好的模型。

迁移学习的好处：你可能不需要进行监督预训练。网络上有很多别人训练好的神经网络，可以下载，你只需要用自己的输出层替换原有的输出层，并微调预训练后的神经网络。

迁移学习的前提：预训练使用的数据、微调使用的数据，两者的类型必须一致。比如，图片对图片，音频对音频，文本对文本。

先在100万（1 million）个数据上预训练神经网络，然后在1000个，甚至50个 数据上进行微调。
神经网络例子：GPT-3、BERTs、ImageNet。这些神经网络都在非常大的图像或文本数据集上训练过，你可以微调它运用到你的应用中。他们也是使用迁移学习的成功案例。

• Machine learning development process 机器学习开发过程 ：Full cycle of a machine learning project 机器学习项目的全周期

MLOps：Machine Learning Operations，机器学习操作。指的是：系统地构建、部署和维护机器学习系统。

机器学习部署举例：浏览器搜索上的语音识别功能，用户对APP说出要搜索的内容，APP录音，并把音频发给部署机器学习模型的服务器，服务器返回语音识别出的文字记录给APP。
Scaling 是指服务器和算法可以扩展规模，能在需要时支撑更多用户比如1百万用户访问。
Logging 是指记录下客户的音频和文字数据，这些数据可以用来训练算法。
System monitoring 是指能够监控某个词被多次读出、某种事情被多次搜索，比如某个名人突然出名，某个政客突然当选，而这个人的名字，由于算法没有训练过，导致无法给出准确的拼写，这时需要使用这个名字的音频再次训练算法。
Model updates 是指把再次训练后的算法，更新到服务器上。

• Machine learning development process 机器学习开发过程 ：Fairness , bias , and ethics 公平、偏见和道德
  

一个简单的风险规避计划就是恢复到我们已知的合理公平的早期系统版本。

• skewed datasets (optional) 倾斜数据集（可选）：Error metrics for skewed datasets 倾斜数据集的错误度量

普通分类（非倾斜数据集）的评价指标：Accuracy 准确率。
Accuracy = $\frac{TP+TN}{TP+FP+FN+TN}$ 。

对于倾斜数据集，即正负样本数量差距大的数据集。比如一种罕见的疾病，所有人中有0.5%的人得病，99.5%的没得病，或者所有人中25%得病，75%没得病。需要使用下方这种评价指标。
倾斜数据集评价指标：Precision 精确率、Recall 召回率。
Precision = $\frac{TP}{TP+FP}$ 。被预测是正样本的里，有多少是真的正样本。
Recall = $\frac{TP}{TP+FN}$ 。实际的正样本里，有多少被预测出来了。

帮助记忆的方法：
TP : True Positive，正确检测（T）为正样本（P）的样本。
FP : False Positive，错误检测（F）为正样本（P）的样本。
FN : False Negative，错误检测（F）为负样本（N）的样本。
TN : True Negative，正确检测（T）为负样本（N）的样本。

• skewed datasets (optional) 倾斜数据集（可选）：Trading off precision and recall 权衡精确率和召回率

之前把分类0、1的阈值定为0.5，$f_{\vec{w},b}(\vec{x})$ ≥ 0.5就预测y=1，$f_{\vec{w},b}(\vec{x})$ < 0.5就预测y=0。现在根据情况定阈值。
当高置信度才预测y=1时，就把阈值定0.7、0.9这样大于0.5的数。阈值越大，就有更高的精确率、更低的召回率。
当要避免错过正样本，只要有可能y=1，就预测y=1时，就把阈值定为0.3这样小于0.5的数。阈值越小，就有更低的精确率、更高的召回率。

在数学中，F1 score 的方程 $\frac{1}{\frac{1}{2}(\frac{1}{P}+\frac{1}{R})}$ 也被称为P和R的调和均值（the harmonic mean of P and R）。调和平均数是一种取平均值的方法，它更强调较小的值。
权衡精确率和召回率的方法，就是使用F1 score，选择使用F1 score最大的那个算法，下图中是算法1。

在许多商业生产环境使用的先进技术中，吴恩达任务最重要的机器学习模型是：神经网络、决策树。

• 实验：D:\Desktop\机器学习\2022-Machine-Learning-Specialization-main\Advanced Learning Algorithms\week3\8.Practice Lab Advice for applying machine learning/C2_W3_Assignment.ipynb 。里的误差计算公式。

线性回归模型的Error计算：
$$J_{\text{test}}(\mathbf{w},b)=\frac{1}{2m_{\text{test}}}\sum _{i=0}^{m_{\text{test}}-1}(f_{\mathbf{w},b}({\mathbf{x}}_{\text{test}}^{(i)})-y_{\text{test}}^{(i)}{)}^2\text{\hspace{1em}(1)}$$

分类模型的Error计算：
$$J_{cv}=\frac{1}{m}\sum _{i=0}^{m-1}\{\begin{array}{ll}1,& \text{if y^(i)=y(i)}\\ 0,& \text{otherwise}\end{array}$$

第四周：Decision Trees 决策树

• Decision Trees 决策树：Decision Tree Model 决策树模型

找完实习后，
接下来直接看CNN这部分，机器学习剩下部分不看了：(强推|双字)2021版吴恩达深度学习课程Deeplearning.ai。第四课01 - 1.1计算机视觉+卷积神经网络CNN_哔哩哔哩_bilibili 。

然后，继续搞毕设，把低清转高清的代码看懂。