自动驾驶路径跟踪控制方法

自动驾驶应用中的路径跟踪控制

摘要

自动驾驶汽车正逐渐成为一种融合工业与学术领域的成熟现实，其影响已延伸至社会和政府层面，远超汽车工程范畴。本文旨在为配备线控转向和线控驱动技术的自动驾驶汽车设计一种自动转向控制方法。通过计算转向动作，使车辆能够跟踪存储在数字地图中的参考路径，该数字地图经过专门构建以支持实时访问。基于参数状态法（PSA）设计了比例+微分（PD）控制策略，并结合前馈（FF）项以提升转弯工况下的路径跟踪控制性能。最后给出了若干实验测试结果，验证了所提出控制器的有效性。

关键词

路径跟踪控制 · Autonomous转向 · Steer-by-线控实验测试

1 引言

“自动驾驶”是一个通用术语，用于指代一种能够在城市和/或高速公路场景下无需或仅需部分人工干预即可行驶的非常规车辆。为了提供统一的术语，[1]定义了从无自动化（0级）到完全自动化（5级）的不同驾驶自动化等级。本文重点研究并开发用于自动转向控制以实现路径跟踪目的的应用中的控制层。路径跟踪控制是机器人控制领域中一个众所周知的课题[2,3]。针对自动驾驶已开展大量实验测试[4,5]，其中参考路径通常通过感应电缆或磁性标记提供，但关于全球定位系统（GPS）的新技术已提高了位置精度。针对自动路径跟踪控制设计了多种反馈控制器，这些控制器通常可分为两个独立类别。

第一类包括所有基于简单几何关系的方法，这些方法利用车辆运动学模型（即通过近似为零）

前后轮胎的侧滑角Pure Pursuit算法，其目标是计算连接车辆位置与参考路径上预设目标位置的弧线曲率，该目标位置位于指定的前视距离处look-ahead距离的参考路径上[6,7]。

第二类涉及基于简化线性单轨模型的所有反馈控制器，该模型考虑了前后轴不同的侧滑角，并提供了阻尼和刚度系数随车速变化的二阶横摆动力学；比例积分微分（PID）是最常用于转向角评估的控制逻辑：一种在横向偏差误差上的PD结构，加上航向误差上的P控制，由[8]设计，证明偏航角误差的贡献进一步提升了跟踪性能，这一点也被[9]所证实，其中仅考虑横向位置误差，结果明显较差。由[10]展示了前馈贡献所带来的优势，可避免选择过高的反馈控制增益，从而也表明其在稳定性与跟踪性能之间的权衡方面的重要性。在[11]中，根据参数状态方法[12],为自动驾驶公交车的路径跟踪问题设计了一种PIDD2控制器，以确保在特定范围内对车速和质量变化具有鲁棒性。同样的参数状态方法被[13,14]用于自动驾驶乘用车。日产（Nissan）[9]提出了一种线性二次型调节器（LQR），并与PD控制器进行了比较。最后，其他控制器结构还采用了滑模控制[15]、 H∞[16]以及模型预测策略[17]。

本文除引言和结论外共分为七个部分：第2节介绍自动驾驶演示车；第3节介绍包含转向动力学的单轨模型；第4节简要介绍用于参考路径生成的数字地图；第5节重点介绍路径跟踪控制设计，该设计最终在第6节中实现并进行了实验验证。

2 自主演示车辆

用于动力学模型验证和控制标定的车辆演示装置是一辆福特Fusion混合动力车，该车通过安装Dataspeed的线控转向、线控油门和线控制动接口被改装为自动驾驶汽车，如图1所示。Dataspeed模块通过CAN总线通信与dSpace微自动箱电子单元连接，用于控制转向角、加速度和制动动作，并测量转向及油门/刹车踏板位置。车辆上安装了多种传感器（德尔福ESR雷达、Velodyne VLP‐16激光雷达、Mobileye摄像头和OXTS xNAV550 RTK GPS），以监测外部环境。

在当前的应用中，仅使用差分GPS作为车辆定位的传感器，为路径跟踪控制器提供反馈输入，并通过UDP协议与微自动箱通信。

3 车辆建模与实验验证

本节重点介绍车辆线性单轨模型和转向动力学方程，这些模型将通过图1所示的车辆演示装置进行实验验证。

3.1 单轨模型

单轨模型（STM）的假设为：
1. 假设车辆为具有质量 m和惯性矩 Jz的刚体
2. 车速 V为常数˙
3. 仅考虑两个自由度（偏 yaw 角速度 r= ψ和侧滑角 β）
4. 车辆侧滑角 β、轮胎滑移角αi和偏航角加速度 r˙足够小，可认为车辆动力学处于线性范围
5. 前轮转向角 δw较小

两个自由度方程可以表示为（见图2）：

$$
\begin{cases}
mV(\dot{\beta} + r) = F_y \
J_z \dot{r} = M_z
\end{cases}
\quad (1)
$$

其中 $F_y$ 和 $M_z$ 是用车辆参考坐标系表示的总侧向力和横摆力矩：

$$
\begin{cases}
F_y = \sum_{\forall i} F_{xi} \sin(\delta_i) + \sum_{\forall i} F_{yi} \cos(\delta_i) \approx \sum_{\forall i} F_{xi} \delta_i + \sum_{\forall i} F_{yi} \
M_z = \sum_{\forall i} F_{xi} \sin(\delta_i)x_i + \sum_{\forall i} F_{yi} \cos(\delta_i)x_i \approx \sum_{\forall i} F_{xi} \delta_i x_i + \sum_{\forall i} F_{yi} x_i
\end{cases}
\quad (2)
$$

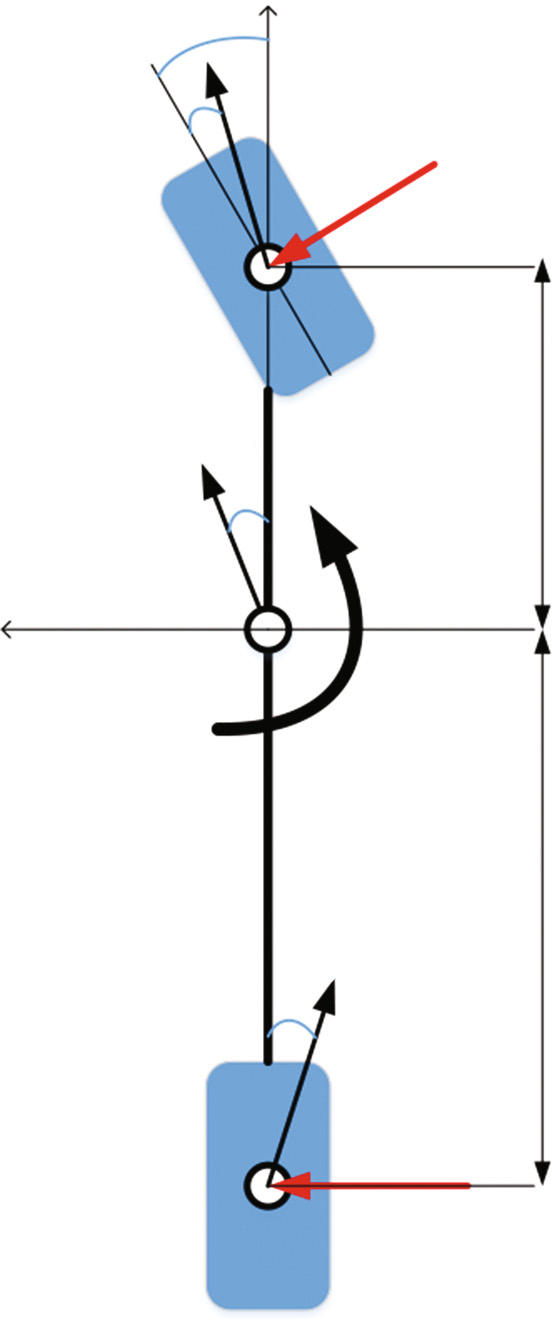
其中 $F_{xi}$、$F_{yi}$ 是作用在 $i$th车轴上的力分量，$x_i$、$y_i$ 为其轴心坐标。在(2)中，忽略了阻力和自对准偏航力矩，并通过考虑车轮转向角的较小值对三角函数进行线性化处理。$\delta_i$ 轮胎侧向力 $F_{yi}$ 取决于多个变量，如轮胎滑移角、轮胎垂直力、路面接触摩擦系数以及轮胎滑移率。为了获得线性化模型，可按以下方式计算：$F_{yi} = C_i \alpha_i$ 其中 $C_i$ 为 $i$th车轴（而非单个车轮）的侧偏刚度。前后轴的等效滑移角 $\alpha_F$ 和后轴 $\alpha_R$ 的等效滑移角可通过车轮参考系中的几何关系按下述公式计算：

$$
\begin{cases}
\alpha_F = \delta_F - \beta - \frac{a}{V} r \
\alpha_R = -\beta + \frac{b}{V} r
\end{cases}
\quad (3)
$$

其中 $a$ 和 $b$ 分别为车辆前后半轴距。线性化单轨车辆模型的最终方程为：

$$
\begin{cases}
mV(\dot{\beta} + r) = (-C_F - C_R)\beta + \left(-\frac{C_F a}{V} + \frac{C_R b}{V}\right)r + C_F \delta_F \
J_z \dot{r} = (-C_F a + C_R b)\beta + \left(-\frac{C_F a^2}{V} - \frac{C_R b^2}{V}\right)r + (C_F a)\delta_F
\end{cases}
\quad (4)
$$

这是一个关于 $\beta$ 和 $r$ 的两个一阶微分方程的系统，以转向角 $\delta_F$ 作为系统的输入。部分单轨模型参数（$m$、$J_z$、$a$ 和 $b$）通过在车辆上的特定试验台测量获得，而前轮 $C_F$ 和后轮 $C_R$ 侧偏刚度值则假定为常数并适当调校，以实现模型与实验数据之间的最佳拟合。在平坦路面（无坡度角）和高摩擦条件下执行斜坡转向和阶跃转向操作，用于验证

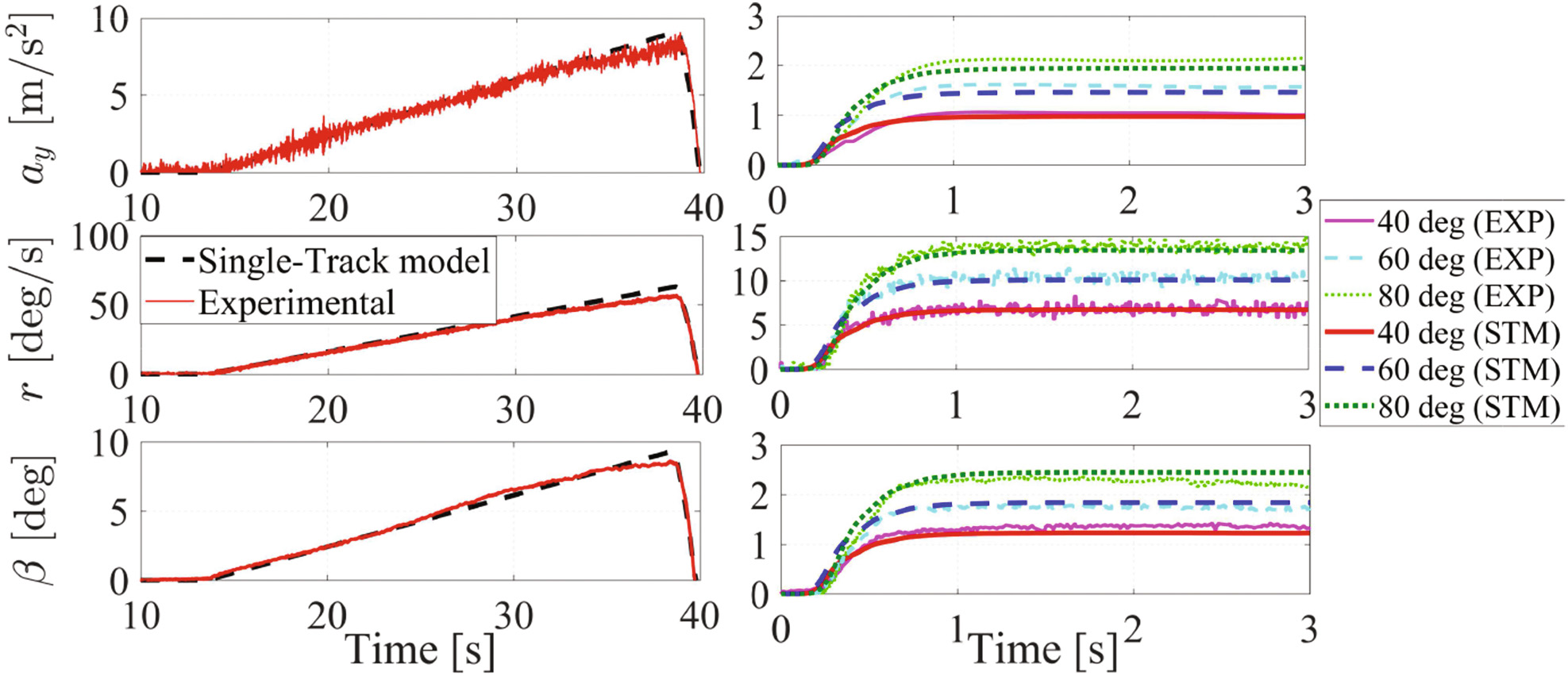
单轨模型。斜坡转向操作（在30km/h的恒定车速下逐渐增加转向角）有助于观察车辆在整个横向加速度范围内的静态横向行为。阶跃转向操作通常用于分析车辆的瞬态行为，因为它是在30公里/小时的恒定车速下施加一个瞬时恒定的转向动作。图3中给出了实验数据与单轨模型输出在偏航角速度、侧滑角和横向加速度方面的比较示例。

3.2 转向动力学

线控转向系统由一个直接连接到转向柱的电动机组成，能够提供期望的角位置。通过扫频测试（SFT）对转向执行进行系统辨识分析，以绘制输出信号 $\delta_{Out}$（测量的转向角位置）与期望转向指令 $\delta_{In}$ 之间的频率响应函数（FRF）。该扫频测试（SFT）包括施加一个具有恒定幅值和可变频率（线性时变）的正弦转向指令。

$$
\begin{cases}
\delta_{In} = \delta_0 \sin(2\pi f(t)t) \
f(t) = f_0 + \frac{f_T - f_0}{T} t
\end{cases}
\quad (5)
$$

其中 $f_0 = 0.001 \text{Hz}$ 是初始时刻的频率 $t_0$，而 $f_T = 5\text{Hz}$ 是时间 $T = 100 \text{s}$ 时的频率。通过使用 MATLAB 的系统辨识工具箱© R,，考虑了不同的传递函数结构，并在极点和零点数量方面进行了比较，如图4所示。一阶传递函数即使引入一个适当设计的零点，也无法匹配实验频率响应函数的幅值和相位滞后；二阶传递函数可以更好地描述系统响应，最高可达 2Hz 的频率，且引入两个零点可改善相位延迟

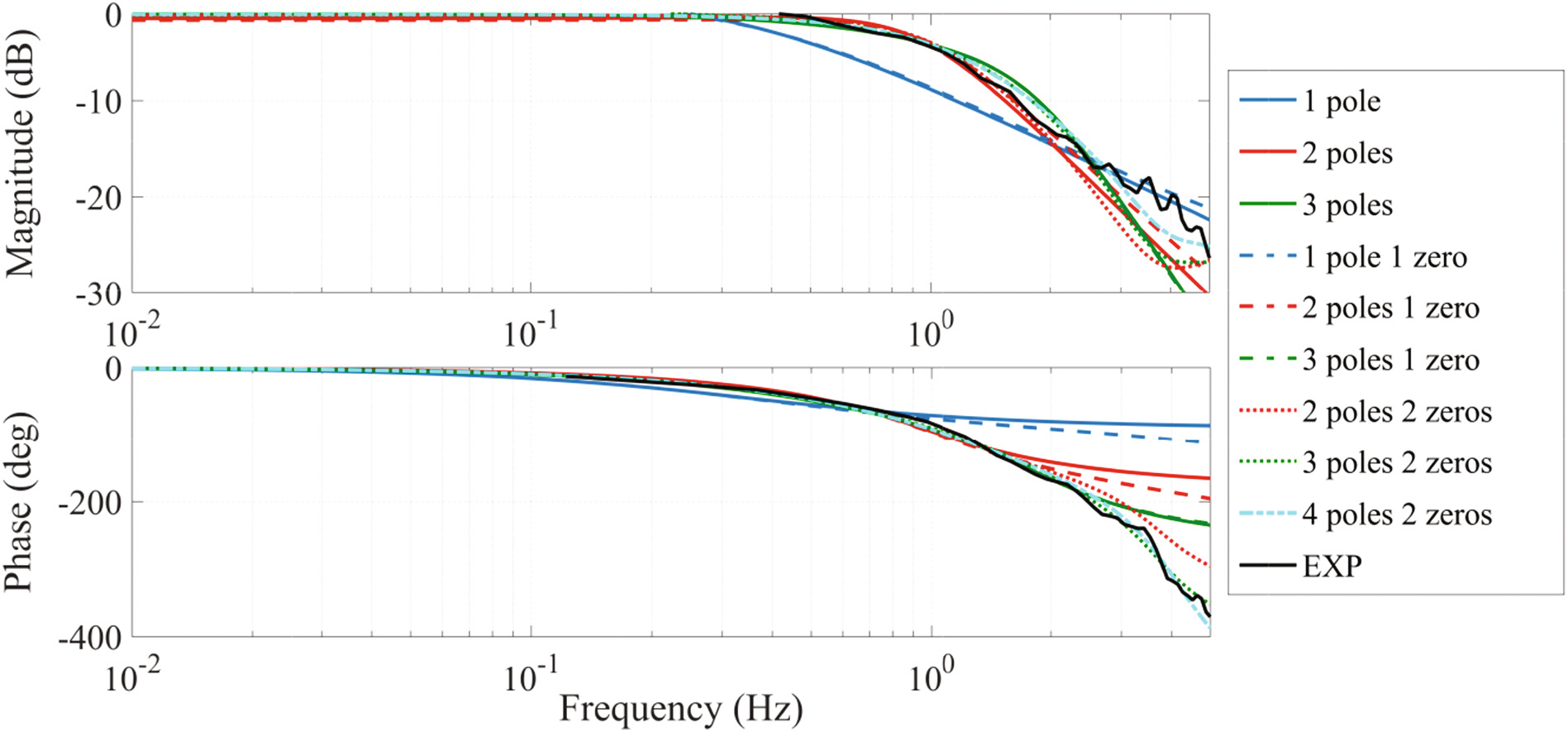
识别，但对高频值的幅值有负面影响。最终选择一个具有2个零点的 4th阶传递函数作为描述实际系统在最高工作频率条件5赫兹下的良好线性模型：

$$
H(s) = \frac{\delta_{Out}}{\delta_{In}} = \frac{n_2 s^2 + n_1 s + n_0}{n_4 s^4 + n_3 s^3 + n_2 s^2 + n_1 s + n_0}
\quad (6)
$$

3.3 侧向偏差方程

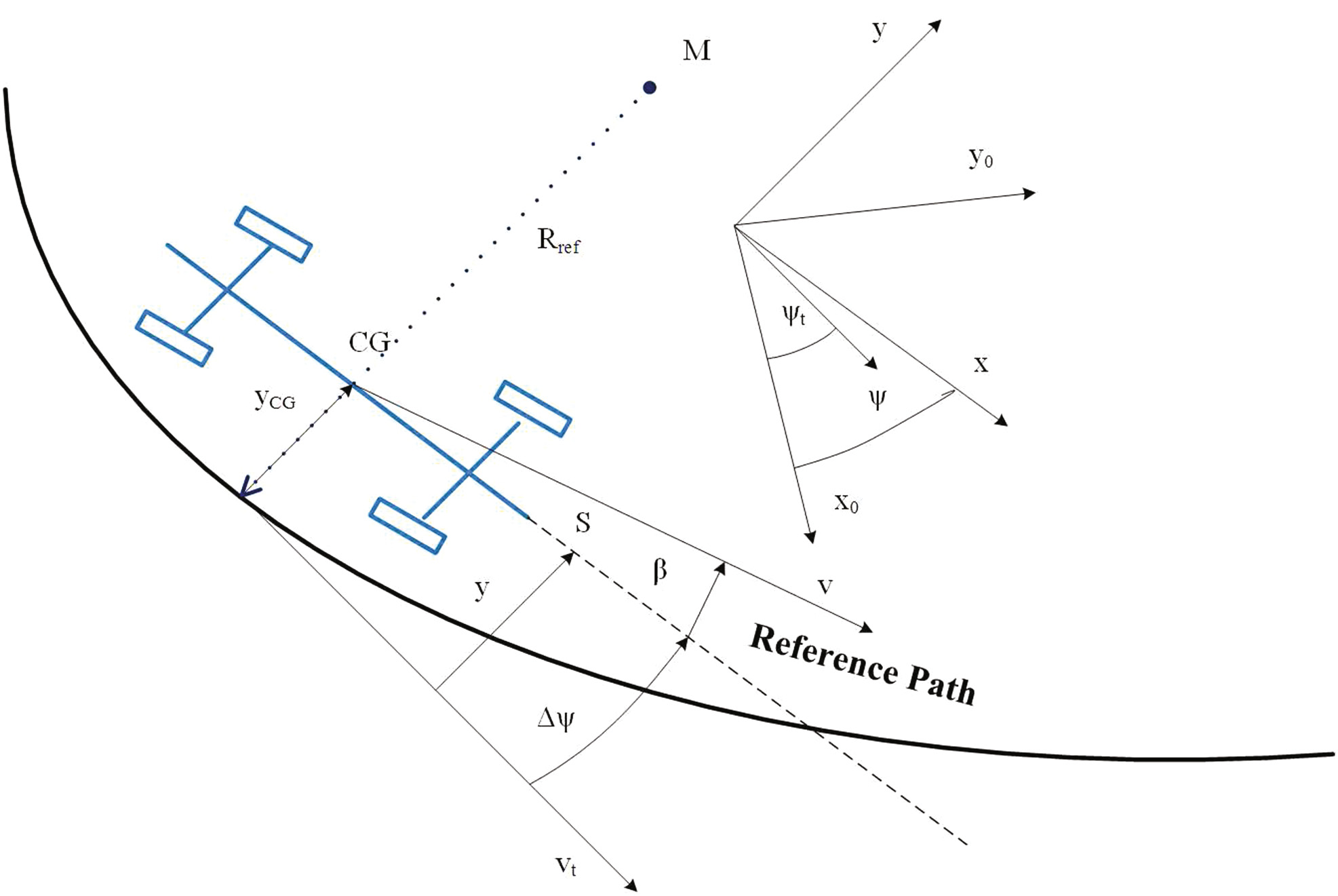
对于路径跟踪控制设计，转向模型必须扩展为不仅包含速度（$\beta$ 和 $r$），还包括车辆航向及其相对于参考路径的侧向位置。图5显示了惯性坐标系 $x_0$、$y_0$ 以及车体固定坐标系 $x$、$y$，该坐标系绕偏航角 $\psi$ 旋转。车速 $V$ 垂直于 $V_t$ 的分量等于 $y_{CG}$ 的变化率。该垂直分量表示为 $V \sin(\beta + \Delta\psi)$，其中 $\Delta\psi = \psi - \psi_t$ 是路径切线与车辆 x轴之间的夹角。通过线性化 $\sin(\beta + \Delta\psi) \approx \beta + \Delta\psi$，质心处的侧向偏差 $y_{CG}$ 按以下方式进行变化：

$$
\dot{y}_{CG} = V(\beta + \Delta\psi)
\quad (7)
$$

在所谓的preview distance $l_s$ 处的距离 $y$ 被视为控制器输入而非 $y_{CG}$，因为它是一个预测变量，从而提高了路径跟踪控制策略的及时性。预览横向偏差可表示为：

$$
y = y_{CG} + l_s \sin(\Delta\psi) \approx y_{CG} + l_s \Delta\psi
\quad (8)
$$

随着 $\dot{y}_{CG}$ 以及车辆偏航角速度 $r = \dot{\psi}$ 的影响而变化，新的位移 $y$ 的变化率为：

$$
\dot{y} = V(\beta + \Delta\psi) + l_s \dot{\Delta\psi} = V(\beta + \Delta\psi) + l_s r - l_s \dot{\psi}_t
\quad (9)
$$

其中 $\dot{\psi} t = V/R {ref} = V \rho_{ref}$ 是路径切线在稳态圆周转向下的偏航角速度。

最终，通过将(9)与单轨模型和转向响应方程(4)及(6)相结合，可得到扩展横向偏差模型。由于引入了(9)，参考曲率 $\rho_{ref}$ 作为除转向角 $\delta_{In}$ 之外的第二个输入出现在系统中。

4 数字地图生成

参考路径被离线转换为数字地图，如[14]中所述，该过程包括将参考路径划分为预定数量的段，每一段通过距离参数 $\gamma$ 的三阶参数多项式进行近似。

$$
\begin{cases}
X_i(\gamma) = a_{Xi} \gamma^3 + b_{Xi} \gamma^2 + c_{Xi} \gamma + d_{Xi} \
Y_i(\gamma) = a_{Yi} \gamma^3 + b_{Yi} \gamma^2 + c_{Yi} \gamma + d_{Yi}
\end{cases}
\quad (10)
$$

其中 $\gamma$ 是轨迹参数，其值在第I段从0变化到1，在第II段从1变化到2，依此类推直至最后一段。$a_{Xi}, b_{Xi}, c_{Xi}, d_{Xi}$ 和 $a_{Yi}, b_{Yi}, c_{Yi}, d_{Yi}$ 分别是第 X段的 Y 和 ith分量的多项式系数。多项式系数的确定通过求解一个约束最小二乘问题实现，该问题保持了路径、路径切线及其瞬时曲率的连续性。图6展示了路径分段的一个示例，并与原始数据点集进行了比较。数字地图能够很好地描述实际数据集，且具有使用数据量显著减少的优势，其数据量仅取决于所选择的段数，而不再与原始数据点的数量相关联。

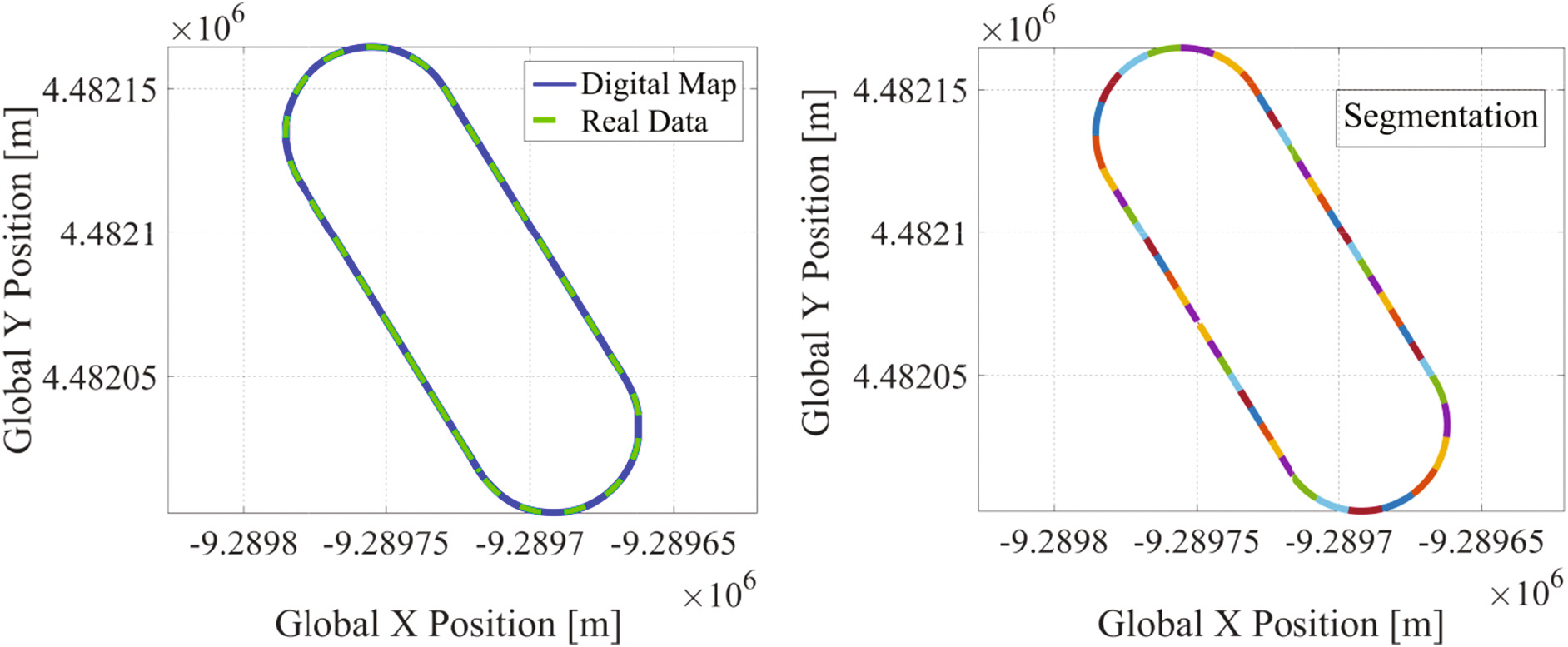
5 路径跟踪控制

本节旨在描述一种PD+FF路径跟踪控制方法，以使预览横向偏差尽可能小，即使在参考曲率变化 $\rho_{ref}$ 的情况下也是如此。

5.1 基于参数状态方法的PD设计

赫尔维茨和伽马稳定性概念如[12]所示，其在自动转向中的应用在[14]中有所报道。在本节中，PSA方法被扩展用于结合转向动力学方程的单轨模型。对式 (4)、(6) 和 (9) 应用拉普拉斯变换后，得到预览横向偏差与输入转向角之间的如下传递函数：

$$
\frac{y(s)}{\delta_{In}(s)} = G(s) = \frac{(C_F J_z V^2 + l_s C_F a m V^2)s^2 + (C_F C_R V b l + l_s V C_F C_R l)s + V^2 C_F C_R l}{s^2 \text{Den}(s) H(s)}
\quad (11)
$$

其中 $\text{Den}(s) = m V^2 J_z s^2 + (C_F V J_z + C_R V J_z + C_F a^2 m V + C_R b^2 m V)s + C_F C_R l^2 + m V^2 b C_R - m V^2 a C_F$。控制器结构采用PD控制逻辑，$\delta_{In}(s) = K_P + K_D s$，其中 $e(s) = y_{ref} - y$。考虑名义车辆参数和15 km/h恒定速度，参考横向偏差 $y_{ref} = 0$ 与实际横向偏差 $y$ 之间的闭环传递函数的多项式可表示为控制器增益 $p(s, K_P, K_D)$ 的函数。在图7中，在 $K_P - K_D$ 平面上评估了实根边界(RRB)、无穷根边界(IRB)和复根边界(CRB)，通过将 $p(s, K_P, K_D)$ 的 $s$ 变量限制在左半平面以满足赫尔维茨稳定性，以及限制在D稳定区域以满足伽马稳定性。根据赫尔维茨稳定性的RRB和CRB边界用灰色线标出，从而将

稳定区域（阿尔冈德‐高斯平面的左半部分）与不稳定区域：采用该方法时，若任务仅要求闭环系统稳定性，则可采取较为保守的控制器增益选择。在许多控制器设计中，仅保证稳定性不足以满足特定应用需求，还需满足更多性能指标，而伽马稳定性概念有助于通过调节时间（$\sigma_0 = 0.3$）、阻尼系数（$\alpha = 30^\circ$）和带宽（$R_b = 1.3$）的选择来满足特征值的规格要求；其中最关键的参数是带宽约束，因为线控转向系统的截止频率几乎等于1Hz，而其余两项要求 $\sigma_0$ 和 $\alpha$ 可以选择更大的裕度。如图7所示，$\Gamma$ 区域被包含在赫尔维茨区域内，因为伽马稳定性对期望特征值的位置施加了更多限制。位于 $K_P$ 和 $K_D$ 值对所在的 $\Gamma$ 区域内的每一对值均满足横向偏差控制要求。

5.2 静态线性前馈设计

预览横向偏差受两个输入的影响：转向角 $\delta_{In}$ 和参考路径的曲率 $\rho_{ref}$。PD控制逻辑在设计时仅考虑了 $\delta_{In}$ 与 $y$ 之间的传递函数 $G(s)$，仍需进一步改进以纳入曲率 $\rho_{ref}$ 的影响。在本节中，引入并设计了静态线性前馈（FF）方法，考虑到参考路径的曲率可以通过数字地图轻松获取，因为参考路径的各段被近似为三阶多项式，且曲率值由以下公式表示：

$$
\rho_{ref}(p) = \frac{X’_p Y’‘_p - Y’_p X’‘_p}{(X’_p X’_p + Y’_p Y’_p)^{3/2}}
\quad (12)
$$

其中 $X’_p$、$Y’_p$ 分别为 $X_p$ 和 $Y_p$ 相对于 $\gamma_i$ 的一阶导数，而 $X’‘_p$、$Y’‘_p$ 分别为其二阶导数。前馈是一种开环控制，设计用于

以便根据当前的 $\rho_{ref}(p)$ 值提供一个 $\delta_{FF}$ 值，这可以通过反转单轨模型中转向角与车辆曲率之间的稳态关系来获得：

$$
\delta_{FF} = (L + K V^2) \rho_{ref}(p)
\quad (13)
$$

其中 $K = \frac{m}{L} \left( \frac{b}{C_F} - \frac{a}{C_R} \right)$ 表示车辆不足转向梯度，$L = a + b$ 为其轴距。

6 实验测试结果

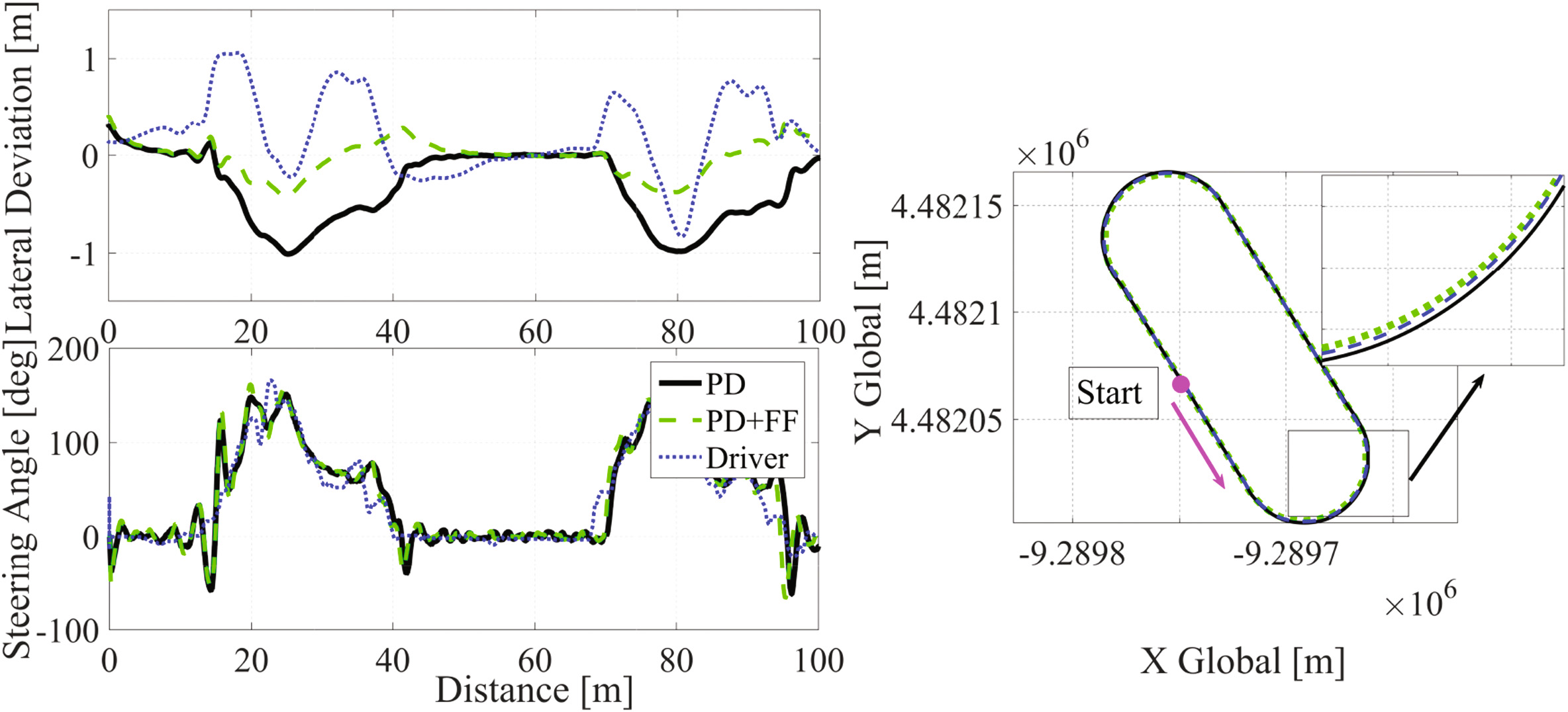
采用参数状态方法设计的PD控制逻辑被加入前馈贡献中，以提供转向角作为图1所示自动驾驶汽车的输入，该车辆需沿图6中的参考路径行驶。车速通过实验调校的比例积分（PI）巡航控制保持在15km/h恒定，此部分不在本文讨论范围内。路径跟踪在自动驾驶模式（PD和PD+FF）以及由普通驾驶员操作的手动模式下执行；结果如图8所示。可以看出，与单独使用PD控制逻辑或驾驶员操作相比，PD+FF控制取得了更好的效果：前馈贡献基于参考曲率 $\rho_{ref}$ 的计算提供了额外的转向作用，能够在单独应用PD控制时改善其性能，特别是在路径的转弯段。

7 结论

本文展示了一种用于路径跟踪控制的自动驾驶转向逻辑的实际应用。采用经过实验验证的单轨线性模型对车辆进行建模，并利用系统辨识方法描述转向动力学。该简单的线性模型能够有效描述横向加速度较低时的车辆横向行为。设计了结合转向动力学和参考路径曲率影响的PD+FF控制策略，并将其应用于配备线控转向技术的车辆演示装置上。在试验场上执行了一项实验性操作，以验证 PD和PD+FF控制器的有效性，并将其性能与人工驾驶进行比较。实验结果证明，即使如此简单的控制器结构，在正常道路条件下（平坦路面且高摩擦系数）也能实现良好的跟踪性能（相对于参考路径的最大误差为50厘米）。