必读！数据挖掘经典8大算法，详细解析，附MATLAB代码

前

言

数据挖掘（Data Mining）是从大量数据中提取出潜在、有价值的信息、模式或知识的过程。它结合了统计学、机器学习、数据库技术、可视化等多学科方法，广泛应用于商业、科研、医疗、金融等领域。

数据挖掘8大经典算法

01

 pearson相关性

        皮尔逊相关系数（Pearson Correlation Coefficient）是一种用于衡量两个连续变量之间线性相关程度的统计量，其值介于-1和1之间。公式如下：

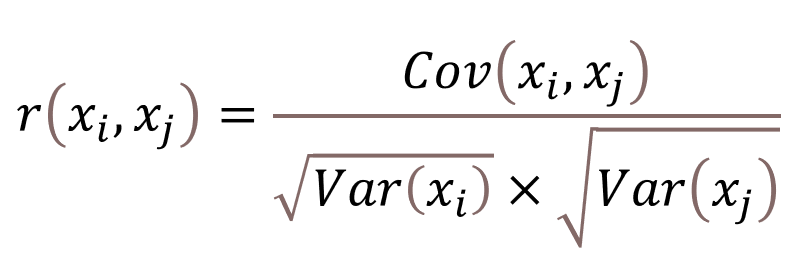
Cov(xi,xj)表示的是协方差 ，Var(xi)表示的是方差，开根号之后就变成了标准差。xi和yi两为个变量的第i个观测值。

皮尔逊相关系数的值在 -1 到 1 之间，值越接近 1 或 -1，表示变量之间的线性关系越强。在实际应用中，通常会对皮尔逊相关系数进行假设检验，以确定观察到的相关性是否具备统计学意义。常见的检验方法是计算t统计量：

    依据自由度和设定的显著性水平，可以通过查阅t分布表来评估相关性是否显著。如果计算出的p值小于设定的显著性水平（如0.05），则拒绝原假设，认为变量间存在显著相关性；反之，若p值大于显著性水平，则无法拒绝原假设，认为相关性不显著。

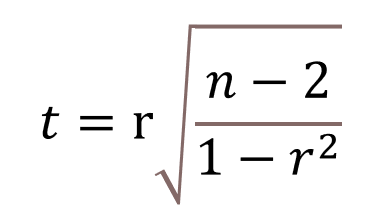
MATLAB代码示例：

% 多变量相关性分析并绘制heatmapclc; clear; close all; % 关闭图形窗口
x = rand(1000,1); %随机生成1列数据y = sin(x)+cos(x); %根据x生成数据yz = tan(y); %根据y生成数据zhz= randn(1000,1); %随机生成数据hzbz = hz.^2+y; %根据hz与y生成bz%% 提取 14 个特征列features = [x,y,z,hz,bz];
%% 计算特征之间的相关性矩阵[corrMatrix,pval]=corr(features,'type','Pearson');%% 绘制热图figure;h = heatmap(corrMatrix, 'CellLabelColor', 'black');h.CellLabelFormat = '%0.3f'; h.FontSize = 9;caxis([-1 1]);  % 设置颜色范围，以便更好地控制图例范围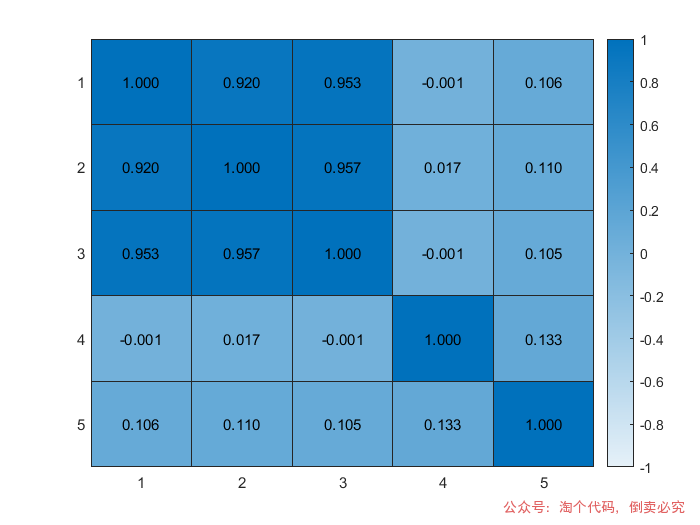

02

 spearman相关性

斯皮尔曼相关系数（Spearman's Rank Correlation Coefficient）是一种衡量两个变量之间的单调关系的统计方法。与皮尔逊相关系数不同，斯皮尔曼相关性不要求数据满足正态分布，而是通过比较数据的秩（排名）来评估变量之间的关系，因此它适用于任何类型的单调关系（无论是线性还是非线性）。

斯皮尔曼相关系数的计算步骤如下：

1. 数据排名：

• 对于每一个变量，将其观测值按照从小到大的顺序进行排序，得到每个值的“秩”。

• 如果数据存在相同的观测值（即重复值），则这些值的秩取为它们的平均秩。

2. 计算秩差：

• 计算两个变量的每个数据点的秩之间的差值。设变量 XX 和 YY 的秩分别为 RXRX 和 RYRY，则每个数据点的秩差为 di=RX(i)−RY(i)di=RX(i)−RY(i)。

3. 计算斯皮尔曼相关系数： 斯皮尔曼相关系数的公式为：

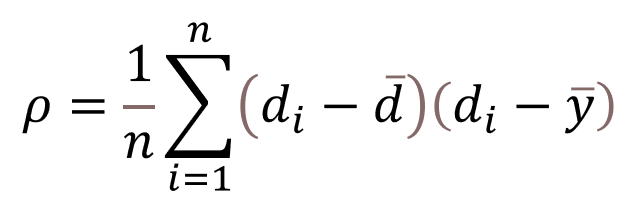
其中，di表示第i个数据对的位次值之差，n代表总的观测样本数。

MATLAB代码示例：

clearclcx = rand(1000,1); %随机生成1列数据y = sin(x)+cos(x); %根据x生成数据y% 对x和y数据分别进行最小-最大归一化x = (x - min(x)) / (max(x) - min(x));y = (y - min(y)) / (max(y) - min(y));% 进行Spearman相关性分析[rho,pval] = corr(x,y,'type','Spearman');% 提取相关系数和p值，因为corr返回的是列向量，直接取第一个元素即可（对于两个变量的情况）rho = rho(1); pval = pval(1); % 绘制散点图并优化样式和颜色scatter(x,y, 20, 'filled', 'MarkerFaceColor',[0.4,0.6,0.8], 'MarkerEdgeColor', 'w');% 设置点的大小为20，填充颜色为一种自定义的蓝色系（RGB值表示），边缘颜色为白色hold on; % 保持图形，后续可以继续添加元素% 设置点的大小为20，填充颜色为一种自定义的蓝色系（RGB值表示），边缘颜色为白色hold on; % 保持图形，后续可以继续添加元素% 添加拟合直线（简单线性回归拟合，仅为了图形更丰富美观，可根据实际情况选择是否添加）p = polyfit(x,y,1); % 拟合一次多项式（直线），得到系数x_fit = linspace(min(x),max(x),100); % 生成用于绘制拟合直线的x值范围y_fit = polyval(p,x_fit); % 根据拟合系数计算对应的y值plot(x_fit,y_fit, 'r', 'LineWidth', 2); % 绘制拟合直线，颜色为红色，线宽为2% 以下开始计算并添加误差带（这里假设误差是拟合直线的预测值上下一定标准差范围，这里简单用均方误差来估算标准差示例，实际可能更复杂）% 先计算拟合直线预测值与实际y值的误差y_predicted = polyval(p,x); % 用拟合直线预测y值residuals = y - y_predicted; % 计算残差（误差）mse = mean(residuals.^2); % 计算均方误差std_error = sqrt(mse); % 估算标准差（简单用均方误差开方）% 计算误差带的上下边界upper_bound = y_fit + std_error;lower_bound = y_fit - std_error;% 绘制误差带，使用较浅的颜色，这里选择淡灰色（RGB值示例，你可按需调整）fill([x_fit,fliplr(x_fit)], [upper_bound,fliplr(lower_bound)], [0.9,0.9,0.9], 'EdgeColor', 'none', 'FaceAlpha', 0.3);% 'EdgeColor', 'none'表示不绘制边缘线，'FaceAlpha', 0.3表示填充颜色的透明度为0.3，即较浅title('Scatter Plot with Spearman Correlation Coefficient and P-value', 'FontSize', 14); % 增大标题字体大小并修改标题xlabel('Normalized x', 'FontSize', 12); % 设置x轴标签及字体大小，这里注明是归一化后的xylabel('Normalized y', 'FontSize', 12); % 设置y轴标签及字体大小，这里注明是归一化后的y% 设置坐标轴刻度字体大小、颜色等样式，将刻度颜色改为黑色set(gca,'FontSize',10,'TickDir','out','TickLength',[0.02 0.02],'XColor','k','YColor','k');% 在图中合适位置添加文本显示相关系数和p值，优化文本样式text(min(x)+(max(x)-min(x))*0.1,min(y)+(max(y)-min(y))*0.9,sprintf('Spearman r = %.3f\np-value = %.3f',rho,pval),...       'FontSize', 10, 'Color', 'black', 'BackgroundColor', [1,1,1,0.8]);  % 修改文本显示内容为Spearman相关系数legend('Data Points', 'Fitted Line', 'Error Band'); % 添加图例说明hold off; % 释放图形，避免后续误操作继续添加元素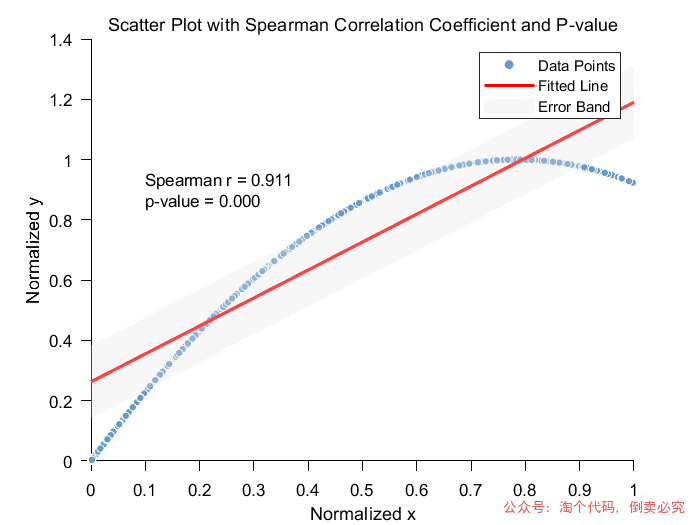

03

主成分分析

    主成分分析是一种统计方法，通过正交变换将一组可能存在相关性的变量转换成一组线性不相关的变量，转换后的这组变量叫主成分。

    PCA的思想是将n维特征映射到m维上(m<n),这m维是全新的正交特征，称为主成分，这m维的特征是重新构造出来的，不是简单的从维特征中减去-m维特征。PCA的核心思想就是将数据沿最大方向投影，数据更易于区分。

主成分分析（PCA）的实现包括几个关键步骤：

1、数据标准化。由于PCA是基于数据的协方差矩阵进行计算的，若不同特征的量纲不同，可能会影响最终结果。因此，通常会对数据进行标准化处理（如零均值、单位方差化），确保每个特征对分析的贡献是平等的。。所采用的标准化公式如下：

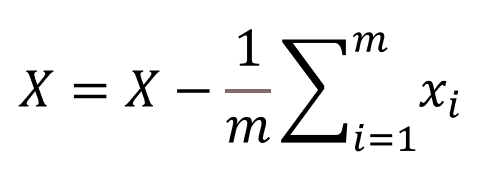
X为X_(n×m)的矩阵。

    2、计算协方差矩阵，标准化后的数据集通常会计算协方差矩阵，该矩阵描述了各个特征之间的关系和方差。协方差矩阵的每个元素表示两个特征之间的协方差。协方差矩阵为：

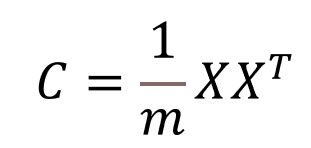
    3、特征值分解。通过对协方差矩阵进行特征值分解，得到特征值和特征向量。特征值表示每个主成分所解释的方差大小，特征向量代表主成分的方向。特征值越大，主成分所包含的信息量越大。

    4、选择主成分。根据特征值的大小选择前几个主成分。通常选择具有最大特征值的几个主成分，它们解释了数据集最多的变异性。

MATLAB代码示例：

clc; 
clear; 
close all; % 关闭图形窗口


x = rand(1000,1); %随机生成1列数据
y = sin(x)+cos(x); %根据x生成数据y
z = tan(y); %根据y生成数据z
hz= randn(1000,1); %随机生成数据hz
bz = hz.^2+y; %根据hz与y生成bz
features = [x,y,z,hz,bz];  %构建特征数据


% data = load('gd.txt'); % 将原始数据保存在txt文件中
data = zscore(features); % 数据标准化


r = corrcoef(data); % 计算相关系数矩阵


% 下面利用相关系数矩阵进行主成分分析，vec1的第一列为r的第一特征向量，即主成分的系数
[vec1, lamda, rate] = pcacov(r); % lamda为r的特征值，rate为各个主成分的贡献率


f = repmat(sign(sum(vec1)), size(vec1, 1), 1); % 构造与vec1同维数的元素为±1的矩阵
vec2 = vec1 .* f; % 修改特征向量的正负号，使得每个特征向量的分量和为正，即为最终的特征向量


num = max(find(lamda > 0.2)); % num为选取的主成分的个数, 这里选取特征值大于0.2的主成分


df = data * vec2(:, 1:num); % 计算各个主成分的得分
tf = df * rate(1:num) / 100; % 计算综合得分


[stf, ind] = sort(tf, 'descend'); % 把得分按照从高到低的次序排列
stf = stf'; 
ind = ind'; % stf为得分从高到低排序，ind为对应的样本编号


% 1. 绘制主成分得分的散点图（假设是二维主成分的情况）
if size(df, 2) == 2 % 如果主成分个数为2才绘制二维散点图
    figure; % 创建新的图形窗口
    scatter(df(:,1), df(:,2)); % 绘制散点图，第一主成分得分作为x坐标，第二主成分得分作为y坐标
    xlabel('第一主成分得分'); % x轴标签
    ylabel('第二主成分得分'); % y轴标签
    title('主成分得分散点图'); % 图标题
end


if num >= 3
    % 计算各个主成分的得分
    df = data * vec2(:, 1:num); % 计算综合得分
    tf = df * rate(1:num) / 100; % 计算综合得分
    
    % 把得分按照从高到低的次序排列
    [stf, ind] = sort(tf, 'descend'); 
    stf = stf'; 
    ind = ind'; 
    
    % 绘制三维主成分得分散点图
    figure; % 创建新的图形窗口
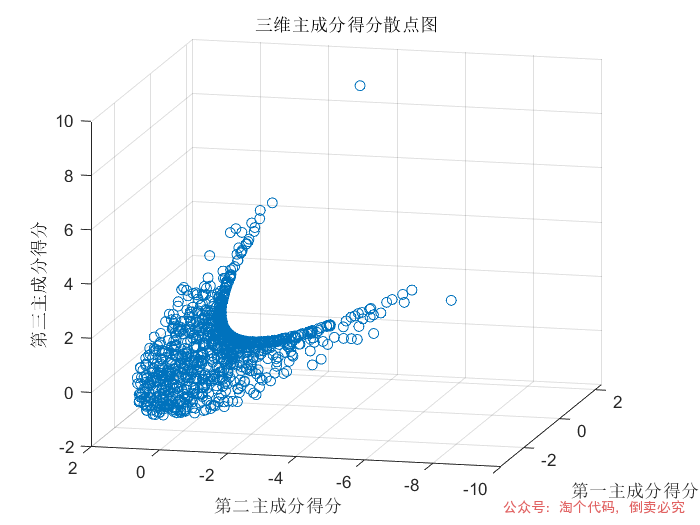
    scatter3(df(:, 1), df(:, 2), df(:, 3)); % 绘制三维散点图，分别以第一、二、三主成分得分作为x、y、z坐标
    xlabel('第一主成分得分'); % x轴标签
    ylabel('第二主成分得分'); % y轴标签
    zlabel('第三主成分得分'); % z轴标签
    title('三维主成分得分散点图'); % 图标题
end


% 以下是新增绘制方差解释图（各主成分贡献率柱状图）的代码
% 生成横坐标标签，即主成分序号（1到选取的主成分个数num）
x_labels = cellstr(num2str((1:num)'));


% 绘制柱状图，展示各主成分的贡献率情况
figure;
bar(1:num, rate(1:num)); % 绘制柱状图，横坐标为1到num的序号，纵坐标为对应主成分的贡献率
xticks(1:num); % 设置横坐标刻度位置
xticklabels(x_labels); % 设置横坐标刻度对应的标签，即主成分序号
xlabel('Principal Components'); % 设置x轴标签为"主成分"
ylabel('Contribution Rate (%)'); % 设置y轴标签为"贡献率（%）"
title('Variance Explanation Chart'); % 设置图表标题为"方差解释图"
grid on; % 显示网格线，让图表更清晰美观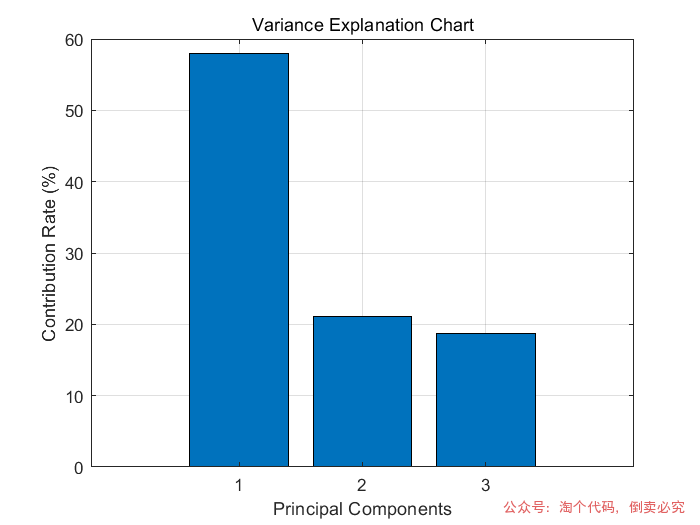

04

K均值聚类分析

从数据集中找出拥有相似属性的数据并将其分成不同的数据子集。和分类分析不同的是聚类分析中没有明显的目标作为数据属性存在。聚类分析算法通过数据检测分析数据的隐藏属性。常见的算法包括分区算法、密度算法、k-means算法、模糊聚类算法等。

这里采用K-means算法对缺陷数据进行分析，其核心思想是将数据集中的n个对象划分为K个聚类，使得每个对象到其所属聚类的中心（或称为均值点、质心）的距离之和最小。这里所说的距离通常指的是欧氏距离：

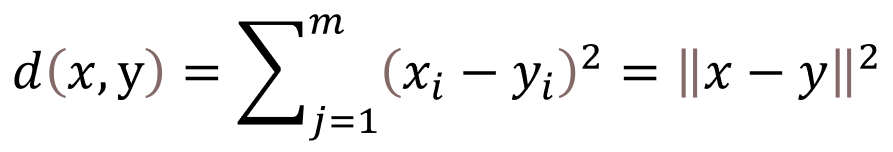
索引j指的是样本点x和 y 的第 j 维。基于这个欧氏距离度量，我们可以将 k-means 算法描述为一个简单的优化问题，即通过迭代的方式最小化簇内平方误差和（Sum of Squared Errors, SSE），有时也称为簇的惯性。

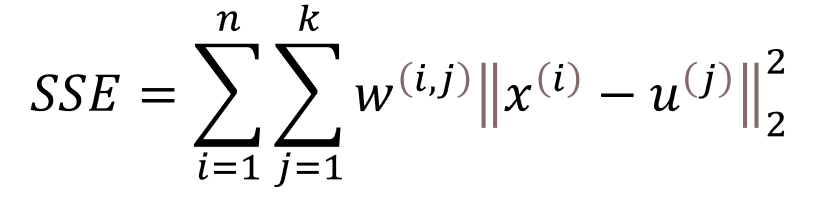
K-means算法的核心思想是通过迭代的方式优化簇内对象与簇质心（中心点）之间的距离之和。算法执行的基本步骤如下：

    1. 初始化：随机选择K个数据点作为初始簇质心。

    2. 分配：计算每个数据点与各簇质心的距离，并将其分配给最近的簇。

    3. 更新：对于每个簇，重新计算簇质心，即取簇内所有数据点的平均值。

    4. 迭代：重复分配和更新步骤，直到簇质心不再发生变化或达到预设的迭代次数。

MATLAB代码示例：

clc; clear; close all; % 关闭图形窗口% 设置随机种子保证结果可复现，这里设置种子值为1rng(1);  
x = rand(1000,1); %随机生成1列数据y = sin(x)+cos(x); %根据x生成数据yz = tan(y); %根据y生成数据zhz= randn(1000,1); %随机生成数据hzbz = hz.^2+y; %根据hz与y生成bzfeatures = [x,y,z,hz,bz];  %构建特征数据data = zscore(features); %标准化数据
% 绘制数据点，以 data 矩阵的第一列作为 X 坐标，第二列作为 Y 坐标绘制散点图scatter(data(:, 1), data(:, 2));  title('数据分布散点图');  % 设置图形标题xlabel('X 坐标');  % 设置 X 轴标签ylabel('Y 坐标');  % 设置 Y 轴标签
% 定义用于绘制聚类结果时区分不同类别的颜色，分别为红、蓝、绿、紫（这里假设 g 代表绿色，m 代表紫色）colors = 'rbgm';  
% 定义用于绘制聚类结果时区分不同类别的形状，分别为圆形、方形、菱形、上三角shapes = 'osd^';  
% 分别绘制 2 类、3 类和 4 类的聚类结果for K = 2:4        % 对数据进行 K-均值聚类，data 为要聚类的数据集，K 为指定的聚类类别数    % idx 存储每个数据点所属的类别编号，C 存储每个聚类簇的中心坐标    [idx, C] = kmeans(data, K);  
    % 创建新的图形窗口，用于绘制当前 K 值对应的聚类结果    figure;      
    % 开启图形叠加绘制模式，后续绘制的内容会叠加在当前图形上    hold on;      
    % 根据数据点所属类别，使用不同颜色和形状绘制聚类结果散点图    gscatter(data(:, 1), data(:, 2), idx, colors(1:K), shapes(1:K), 5);      
    % 绘制聚类得到的每个簇的中心，用黑色的 x 形状标记，设置标记大小和线条宽度使其更明显    plot(C(:, 1), C(:, 2), 'k*', 'MarkerSize', 12, 'LineWidth', 2);      
    % 设置当前图形的标题，表明是类别数为 K 的聚类结果    title(sprintf('K = %d 的聚类结果', K));      
    xlabel('X 坐标');  % 设置 X 轴标签        ylabel('Y 坐标');  % 设置 Y 轴标签    
    % 生成图例，为每个类别生成对应的图例标签，设置图例位置为自动选择较合适的位置    legend(arrayfun(@(i) sprintf('簇 %d', i), 1:K, 'UniformOutput', false), 'Location', 'best');      
    % 结束当前图形的叠加绘制模式    hold off;  end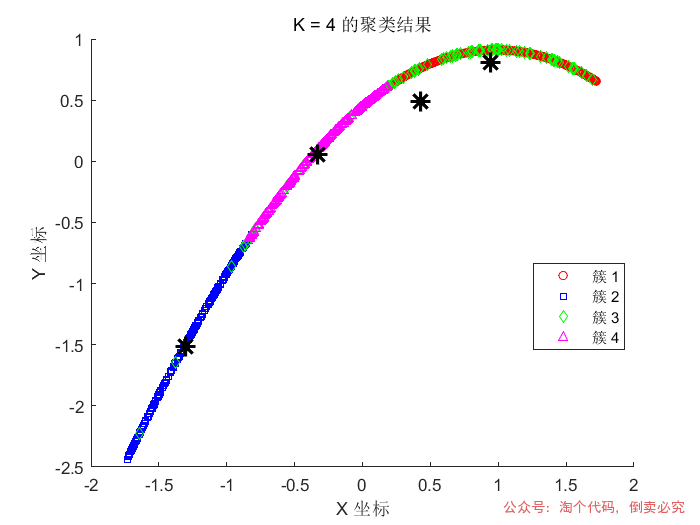

05

DBSCAN聚类分析

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，能够发现任意形状的簇，并有效识别噪声点。其核心思想是：“簇”是数据空间中密集区域，被低密度区域分隔。与K-means不同，DBSCAN不需要预设簇的数量，因此特别适用于数据中簇的数量和形状不明确的情况。

算法流程如下：

1. 1.随机选择未访问点

• 若该点是核心点，则创建一个新簇，并递归扩展其邻域内所有密度可达的点。

• 2.扩展簇

• • 将核心点邻域内的点加入簇，若邻域内的点也是核心点，则继续扩展。

• 3.标记噪声

• • 无法被任何簇包含的点标记为噪声（标签为 -1）。

  MATLAB代码示例：

  % 生成测试数据（2维高斯分布）% rng(1); % 固定随机种子data = [randn(100,2)*0.5 + [2 2];        randn(100,2)*0.5 + [-2 -2];       randn(50,2)*0.5 + [2 -2]];
  
  % 调用DBSCANeps = 0.6;     % 邻域半径minPts = 5;    % 最小邻域点数labels = dbscan(data, eps, minPts);
  % 可视化结果figure;gscatter(data(:,1), data(:,2), labels, 'rgbm', 'o+^s', 5);title('DBSCAN聚类结果');xlabel('X'); ylabel('Y');hold on;noise = data(labels == -1, :);plot(noise(:,1), noise(:,2), 'k*', 'MarkerSize', 5);legend('Cluster 1', 'Cluster 2', 'Cluster 3', 'Noise');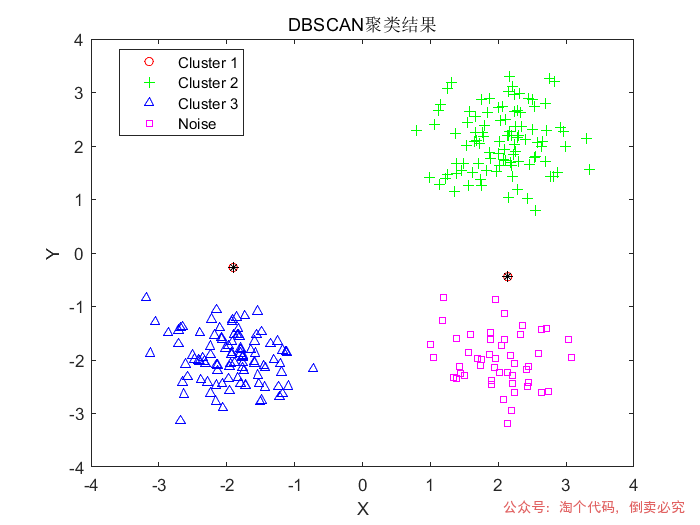

  

  06

  层次聚类分析

  层次聚类（Hierarchical Clustering）是一种基于数据之间的相似性递归构建层次树状结构（也叫做树状图，Dendrogram）的聚类方法。它不需要预先设定聚类的数量，通过不断地合并（自底向上）或划分（自顶向下）数据点形成层次结构。层次聚类方法主要有两种类型：

  凝聚型（Agglomerative）：从每个数据点开始，将最近的两个簇合并成一个簇，直到所有数据点被聚合成一个簇。通常是自底向上的方法。

  分裂型（Divisive）：从所有数据点作为一个簇开始，不断地划分簇，直到每个簇只有一个数据点为止。通常是自顶向下的方法。

  常见的凝聚型层次聚类方法包括：

  单链接（Single Linkage）：合并簇时，选择最近的两个簇，距离为两个簇之间最小的点距离。

  全链接（Complete Linkage）：合并簇时，选择最近的两个簇，距离为两个簇之间最远的点距离。

  均值链接（Average Linkage）：合并簇时，选择最近的两个簇，距离为两个簇之间所有点的平均距离。

  层次聚类的优点：

  不需要预设簇的数量。

  能够发现不同形状的簇结构。

  适用于小规模数据集。

  缺点：

  对于大数据集，计算开销较大（时间复杂度较高）。

  不容易处理噪声数据。

  不适用于需要指定簇数的情况。

  MATLAB中层次聚类的实现

  MATLAB 提供了内建的 linkage 和 dendrogram 函数来实现层次聚类。linkage 函数用于计算数据的层次聚类，并返回一个层次结构（链接矩阵），dendrogram 用于绘制树状图。

  MATLAB代码示例：

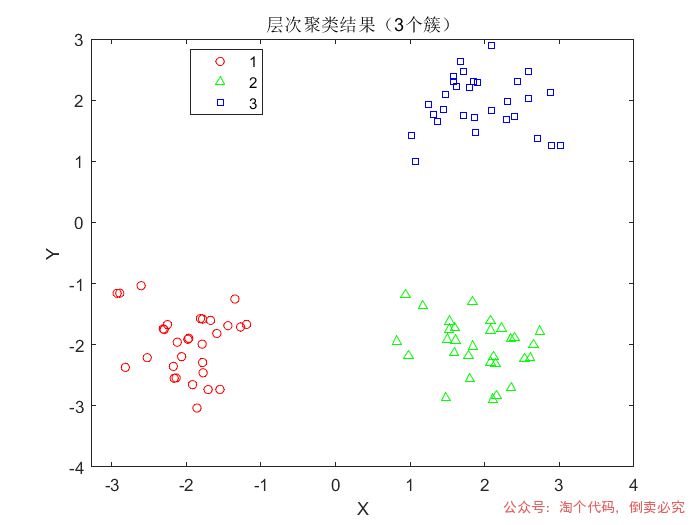
  % 生成测试数据（3个高斯分布簇）rng(1); % 固定随机种子data = [randn(30,2)*0.5 + [2 2];        randn(30,2)*0.5 + [-2 -2];       randn(30,2)*0.5 + [2 -2]];
  % 计算层次聚类树Z = linkage(data, 'ward', 'euclidean'); % 使用Ward方法和欧氏距离
  % 可视化树状图figure;dendrogram(Z);title('层次聚类树状图');
  % 切割树状图生成3个簇cutoff = 3; % 指定簇数labels = cluster(Z, 'MaxClust', cutoff); 
  % 可视化聚类结果figure;gscatter(data(:,1), data(:,2), labels, 'rgb', 'o^s', 5);title('层次聚类结果（3个簇）');xlabel('X'); ylabel('Y');
  % 计算cophenetic相关系数（值越接近1越好）c = cophenet(Z, pdist(data)); fprintf('Cophenetic相关系数: %.4f\n', c);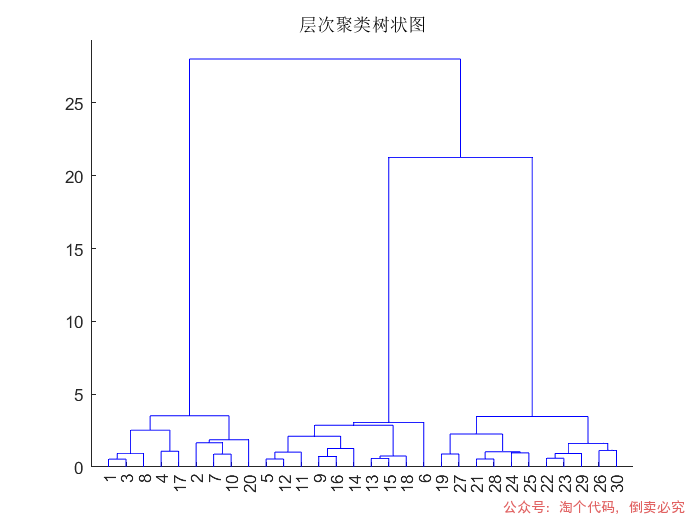

  

  

  07

  关联规则挖掘——Apriori算法t

  Apriori算法是关联规则挖掘的经典算法。关联规则中的待关联事物称为项，项是项集I的组成部分，项集长度用来表示项 在项集中的个数，k-项集就是一个项集中包含k个项，定义待挖掘的样本集Y，是项集 的子集，样本数据库D则囊括了所有样本。支持度和置信度是关联规则的两个重要概 念。在样本数据库D中支持度是指A、B同时出现的概率。记作：

  

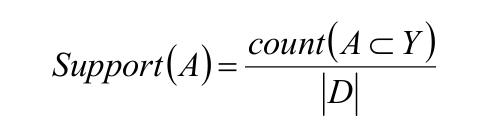
  其中， count (a⊂Y)为样本集Y中A的样本数量，|D|为数据库样本数量。

  关联规则A->B的支持度记作：

  

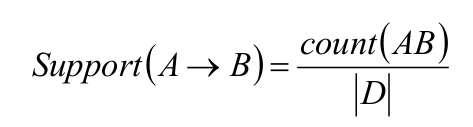
  其中，count(AB)为A、B同时出现的样本数量。

  关联规则A->B的置信度度记作：

  

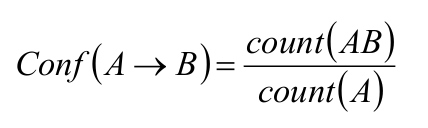
  其中，count(A)为样本Y中出现A的数量。

  MATLAB代码示例：

  clear; clc;
  data = [1 1 0 0 1        0 1 0 1 0        0 1 1 0 0        1 1 0 1 0        1 0 1 0 0        1 1 1 0 1        1 1 1 0 0];min_sup = input("请输入最小支持度(正整数，示例：2)\n");  % 最小支持度(未除以n)min_con = input("请输入最小置信度([0,1]的小数，示例：0.75)\n");  % 最小置信度(已除以n)
  [n, m] = size(data);for i = 1:n    x{i} = find(data(i, :) == 1);  % 求每行购买商品的编号end
  k = 0;while 1    k = k + 1;    L{k} = {};  %% 生成候选集C{k}        if k == 1        C{k} = (1:m)';     else        [nL, mL] = size(L{k-1});        cnt = 0;                for i = 1:nL            for j = i+1:nL                tmp = union(L{k-1}(i, :), L{k-1}(j, :));  % 两集合并集                if length(tmp) == k                    cnt = cnt + 1;                    C{k}(cnt, 1:k) = tmp;                end            end        end                C{k} = unique(C{k}, 'rows');  % 去掉重复的行    end        %% 求候选集的支持度C_sup{k}    [nC, mC] = size(C{k});  % 候选集大小        for i = 1:nC        cnt = 0;        for j = 1:n            if all(ismember(C{k}(i, :), x{j}), 2) == 1  % all函数判断向量是否全为1，参数2表示按行判断                cnt = cnt + 1;            end        end        C_sup{k}(i, 1) = cnt;  % 每行存候选集对应的支持度    end        %% 求频繁项集L{k}    L{k} = C{k}(C_sup{k} >= min_sup, :);          if isempty(L{k})  % 这次没有找出频繁项集        break;    end        if size(L{k}, 1) == 1  % 频繁项集行数为1，下一次无法生成候选集，直接结束        k = k + 1;        C{k} = {};        L{k} = {};        break;    endend
  fprintf("\n");
  for i = 1:k    fprintf("第%d轮的候选集为:", i);     C{i}    fprintf("第%d轮的频繁集为:", i);     L{i}end
  fprintf("第%d轮结束，最大频繁项集为:", k); L{k-1}
  [nL, mL] = size(L{k-1});rule_count = 0;
  for p = 1:nL  % 第p个频繁集    L_last = L{k-1}(p, :);  % 之后将L_last分成左右两个部分，表示规则的前件和后件        %% 求ab一起出现的次数cnt_ab    cnt_ab = 0;    for i = 1:n        if all(ismember(L_last, x{i}), 2) == 1  % all函数判断向量是否全为1，参数2表示按行判断            cnt_ab = cnt_ab + 1;        end    end        len = floor(length(L_last) / 2);    for i = 1:len        s = nchoosek(L_last, i);  % 选i个数的所有组合        [ns, ms] = size(s);                for j = 1:ns            a = s(j, :);            b = setdiff(L_last, a);            [na, ma] = size(a);            [nb, mb] = size(b);                        %% 关联规则a->b            cnt_a = 0;            for i = 1:na                for j = 1:n                    if all(ismember(a, x{j}), 2) == 1  % all函数判断向量是否全为1，参数2表示按行判断                        cnt_a = cnt_a + 1;                    end                end            end            pab = cnt_ab / cnt_a;            if pab >= min_con  % 关联规则a->b的置信度大于等于最小置信度，是强关联规则                rule_count = rule_count + 1;                rule(rule_count, 1:ma) = a;                rule(rule_count, ma+1:ma+mb) = b;                rule(rule_count, ma+mb+1) = ma;  % 倒数第二列记录分割位置(分成规则的前件、后件)                rule(rule_count, ma+mb+2) = pab;  % 倒数第一列记录置信度            end                        %% 关联规则b->a            cnt_b = 0;            for i = 1:na                for j = 1:n                    if all(ismember(b, x{j}), 2) == 1  % all函数判断向量是否全为1，参数2表示按行判断                        cnt_b = cnt_b + 1;                    end                end            end            pba = cnt_ab / cnt_b;            if pba >= min_con  % 关联规则b->a的置信度大于等于最小置信度，是强关联规则                rule_count = rule_count + 1;                rule(rule_count, 1:mb) = b;                rule(rule_count, mb+1:mb+ma) = a;                rule(rule_count, mb+ma+1) = mb;  % 倒数第二列记录分割位置(分成规则的前件、后件)                rule(rule_count, mb+ma+2) = pba;  % 倒数第一列记录置信度            end        end    endend
  fprintf("当最小支持度为%d，最小置信度为%.2f时，生成的强关联规则：\n", min_sup, min_con);fprintf("强关联规则\t\t置信度\n");
  [nr, mr] = size(rule);
  for i = 1:nr    pos = rule(i, mr-1);  % 断开位置，1:pos为规则前件，pos+1:mr-2为规则后件    for j = 1:pos        if j == pos            fprintf("%d", rule(i, j));        else            fprintf("%d∧", rule(i, j));        end    end    fprintf(" => ");    for j = pos+1:mr-2        if j == mr-2            fprintf("%d", rule(i, j));        else            fprintf("%d∧", rule(i, j));        end    end    fprintf("\t\t%f\n", rule(i, mr));end

  

  08

  异常值检测——孤立森林算法

  孤立森林（Isolation Forest）是一种基于树的算法，主要用于检测数据集中的异常值（即离群点）。它通过在数据中生成多颗决策树，利用数据点的“孤立”程度来判断是否为异常值。与传统的基于距离的异常值检测方法不同，孤立森林的主要思想是通过不断“隔离”数据点，较容易被孤立的数据点（即异常值）比那些较难被孤立的数据点更容易被标记为异常。

  >> 孤立森林的原理

  对于每一个数据点，通过随机选择一个特征和该特征的随机切分值来构建树。重复这一过程，直到构建出一颗树。数据点在树中被“隔离”得越早，意味着它可能是异常点。通过多个树来判断一个数据点的异常程度。大多数异常点在树中会被隔离得很早，从而可以通过计算它们在树中被隔离的路径长度来判断其是否为异常值。

  孤立森林的关键概念包括：

  孤立路径长度：数据点从根节点到被隔离的节点的路径长度。路径长度越短，数据点越容易被孤立，通常表示该点是异常值。

  平均路径长度：通过多颗树的平均路径长度来判断数据点的异常性。

  MATLAB代码示例：

  clearclc% 数据准备% 生成一些示例数据，其中包含正常点和异常点data = [randn(100,2); randn(10,2) + 5];  % 100个正常点，10个异常点
  contaminationFraction = single(0.05);  % 设置异常比例 %%  孤立森林进行检测剔除异常值  %%
  [forest, tf_forest, s_forest]=iforest(data, ContaminationFraction=contaminationFraction);outlierIndices = find(tf_forest > forest.ScoreThreshold);
  % 绘制结果figure;scatter(data(:,1), data(:,2), 'b');hold on;scatter(data(outlierIndices, 1), data(outlierIndices, 2), 'r', 'filled');title('Detected Anomalies');xlabel('Feature 1');ylabel('Feature 2');legend('Normal', 'Anomaly');
  data(outlierIndices) = []; 剔除异常值cleanedDate=data;%剔除异常值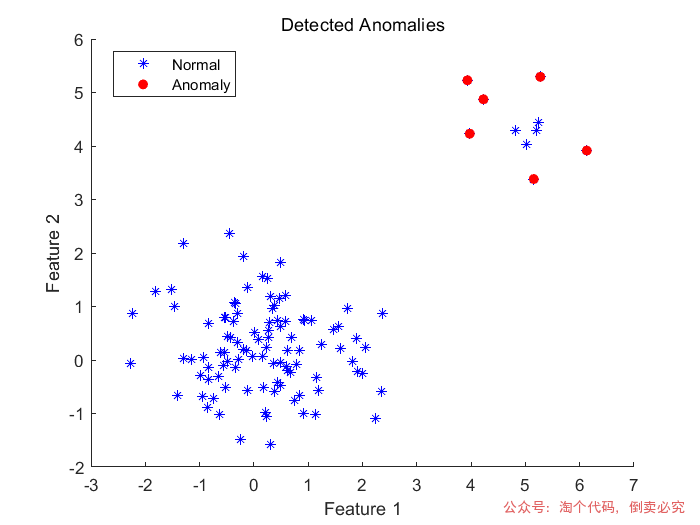

  

  ---

  获取更多代码：