青蒿素优化算法(Artemisinin Optimization,AO)。这一算法的灵感来自青蒿素药物治疗疟疾的过程,其中涉及到全面根除人体内的疟疾寄生虫。该算法包括3个优化阶段:模拟全局搜索的综合淘汰阶段、局部开发的局部清理阶段和增强算法跳出局部最优的后合并阶段。
该成果于2024年发表在工程领域四区期刊Displays上。

青蒿素分子具有某些活性基团,当它们与亚铁离子接触时会发生化学反应。这种相互作用损害疟疾寄生虫的生物膜和内部生物分子,导致细胞膜完整性的破坏并导致膜破裂。与此同时,青蒿素扰乱了疟疾寄生虫的内部生化工作,破坏了它的生存能力。当有人患上疟疾时,从感染到最终用青蒿素缓解的过程遵循一定的路径:
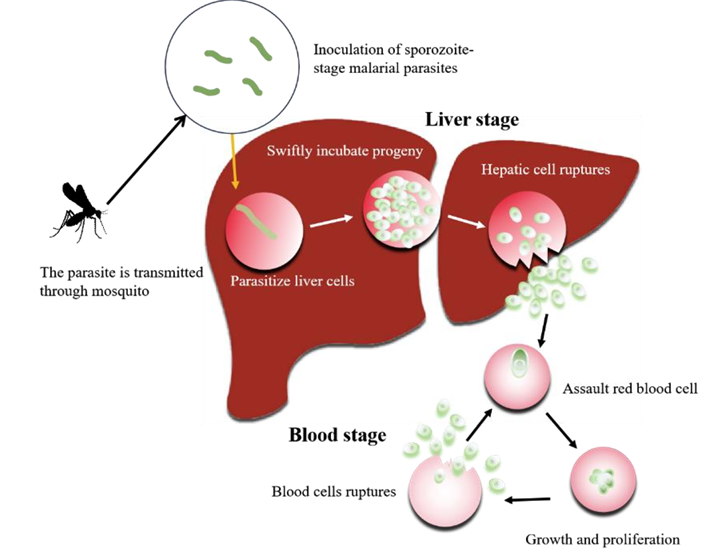
1。感染:疟疾通常是由蚊子叮咬传播的寄生虫引起的。2.疟疾症状发作:疟疾寄生虫进入红细胞后,迅速生长,导致毒素释放,感染者开始出现疟疾症状。3.医疗咨询和诊断:当个人出现疟疾症状时,他们通常会去看医生进行诊断和治疗。4.初步治疗(发病阶段):治疗从发病的最初阶段开始,在此阶段,医疗专业人员给予较高剂量的青蒿素药物,以迅速缓解疟疾症状。5.后续用药:患者定期预约验血,以跟踪疾病的进展。6.中期至晚期治疗(维持阶段):在治疗的初始阶段之后,患者进入维持阶段。7.完全恢复:一旦所有疟疾寄生虫都从患者体内清除,所有症状都消失。
经过一系列的生命周期阶段,大量寄生虫进入血液,红细胞的猖獗感染,进一步复制和毒素释放(活跃期),如图所示。
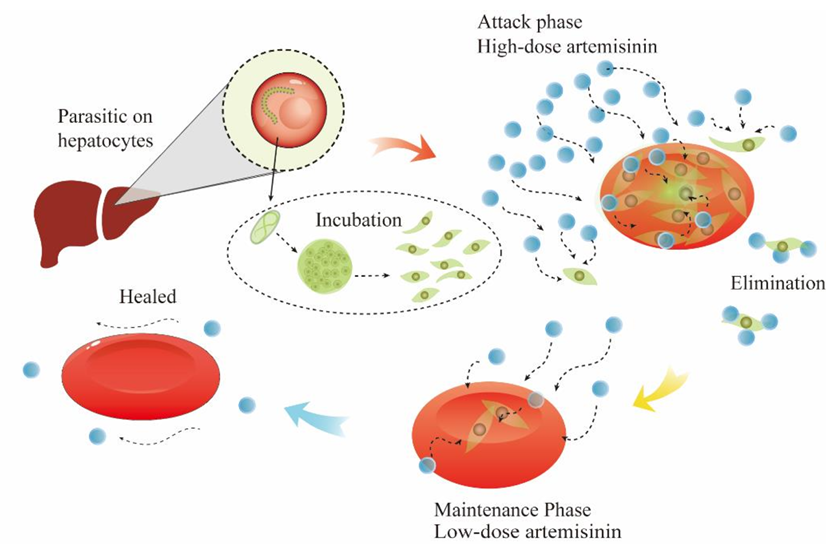
在下图中,在最初的治疗阶段,使用更高剂量的青蒿素药物来控制疟疾症状并迅速减少寄生虫数量。大量的药物通过血液迅速扩散,渗透到整个人体,以寻找最终的解决方案。随后,治疗逐渐进入维持阶段。在这个阶段,药物剂量减少,目的是坚持清除体内任何残留的疟原虫,直到达到最隐蔽的“解决方案”。通过对整个过程的分析,并利用其复杂的细节,本研究提出了青蒿素优化(AO)。
1.原理详解
(1)初始化阶段
患者通过口服或注射将青蒿素药物引入体内。从这一现实中汲取灵感,本文概念化的药物微粒作为搜索代理的算法,这些搜索代理的整个合奏构成算法的解决方案集。最初,初始化整个群体,表示为A。如方程式(1)所述,完整群体N包括搜索代理,其中搜索代理D表示搜索代理内的多维成分。这种现象反映了药物在人体内的分解和吸收,通过血液分散到全身的各个部位。
在方程中,T和B表示解空间的边界,而R表示一组随机数序列,其值范围在[0,1]之间。AO采用了一种常见的方法,在元启发式算法,利用随机数序列生成初始解。
(2)全面淘汰阶段
在疟疾治疗的最初阶段,给病人服用更大剂量的药物,以迅速控制疾病的进展。青蒿素一旦被吸收,就会随着血液输送到人体的各个部位而扩散。药物在体内的分布受血流、血管渗透性和药物与蛋白质的结合亲和力等因素的影响。此外,人体复杂的结构对青蒿素药物构成了巨大的挑战。考虑到这些因素,本节介绍了一个独特的搜索模型来模拟药物扩散的过程,如方程2所示:
在该策略中,搜索代理具有大规模分散的特性,可以作为搜索复杂解空间的向导.这里, +1和 分别代表更新前后的搜索代理,best是当前最优。同时,青蒿素类药物在人体内的扩散遵循药代动力学原理。该策略考虑了药物浓度随时间降低的事实。青蒿素药物浓度的衰减可使用一室模型描述,如下所示:
变量C表示药物浓度,k表示速率常数。C(t)表示时间t时的药物浓度。在该模型中,随着时间的推移,药物浓度C(t)呈指数衰减。因此,青蒿素药物浓度的指数可使用以下公式:
在该策略中,假设初始药物浓度为1,药物衰减率为4,利用算法的评估过程来模拟模型中的时间进程。在这里,f和Maxf表示算法的当前和最大求值迭代。由于患者病情严重程度的变化和生理因素的差异,导致不同的药物剂量和持续时间,患者可能会在此阶段花费不同的持续时间。为了封装这种固有的可变性,引入了概率系数ε,如下式所示:
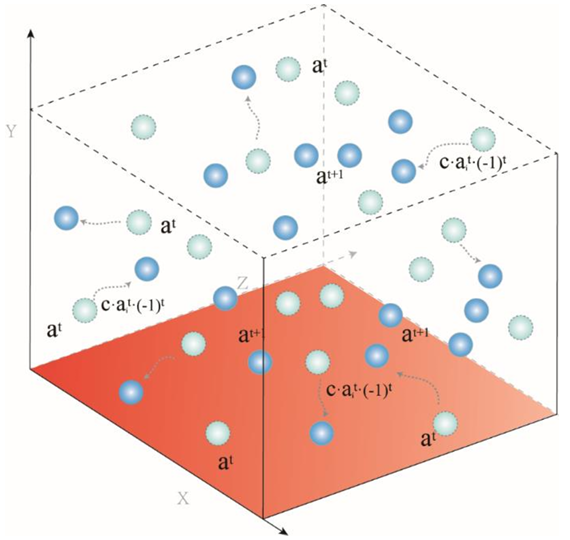
在该等式中,K用作概率系数,结合算法的评估进度来模拟客观场景,其中患者在该阶段基于个体状况表现出不同的反应和持续时间。本节简要模拟每个粒子的运动过程,如下图所示。最后,综合消除阶段策略可以由下式所示:
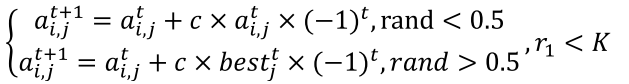
其中,r1是范围为[0,1]的随机数。在最初的治疗阶段之后,随着疾病得到控制,治疗过渡到维持阶段,以确保彻底治愈疟疾。
(3)局部清除阶段
维持阶段的目标是消除体内任何残留的疟原虫,防止它们繁殖和疟疾症状复发。虽然早期治疗通常会迅速缓解症状,但少数疟原虫可能会在体内持续存在,特别是在严重感染的情况下。在这一阶段,患者继续接受较低剂量的青蒿素及其衍生物治疗,以确保彻底根除疟原虫,最大限度地减少人体不良反应的风险。受此启发,本文设计了一种局部清除阶段策略。在这种策略中,粒子的运动过程如下图所示,使用以下公式来确定粒子的位置
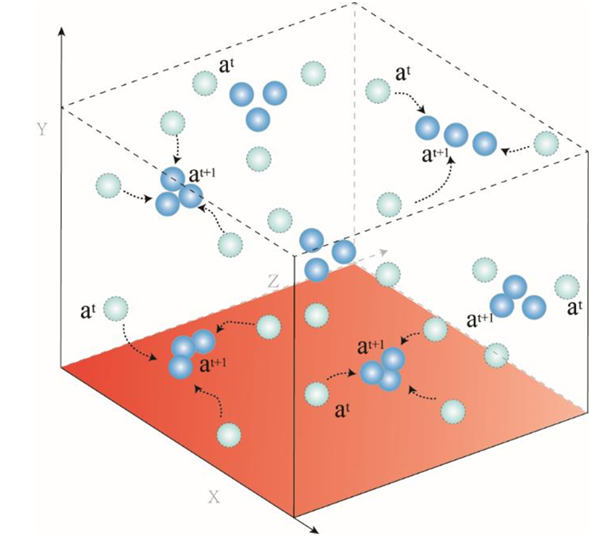
在这个等式中, 表示归一化的适应值,将适应值转换为概率分布,以作为个体之间的相对权重。这有助于在一定程度上保留优秀的个体,同时为表现较差的个体提供机会,调整算法对不同个体的关注。其中,k表示系数,取[0.1,0.6]之间的随机值。这种策略模拟了少量青蒿素清除人体内潜在疟疾寄生虫的过程。
(4)巩固阶段
(5)本部分介绍了巩固阶段的情况,识别意外情况的可能性并模拟这种特定情况。在这种策略中,假设不活跃的寄生虫形式留在人体内。不幸的是,尽管这些休眠的寄生虫继续存在,但一些患者可能会再次出现疟疾。该策略的模型由下式表示:
在这个等式中,besti,j表示当前最佳解在第j维中的子向量。上述公式代表由于进入休眠期而没有被消灭的疟疾寄生虫。如下图所示,该策略增强了搜索代理逃离局部最优的能力。
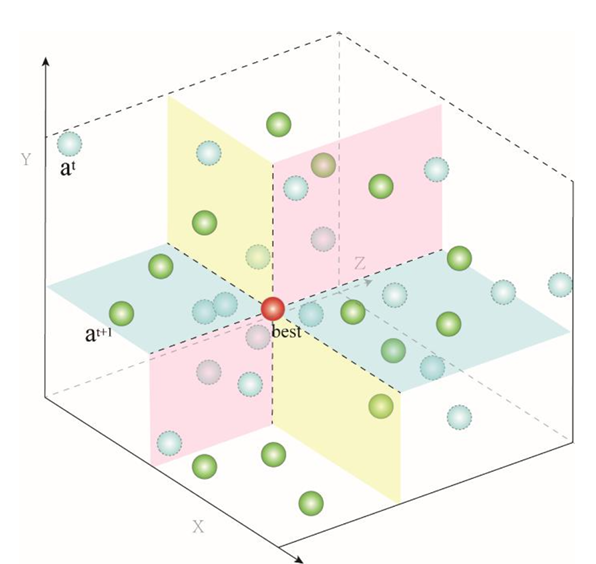
AO算法的流程框图如下图所示
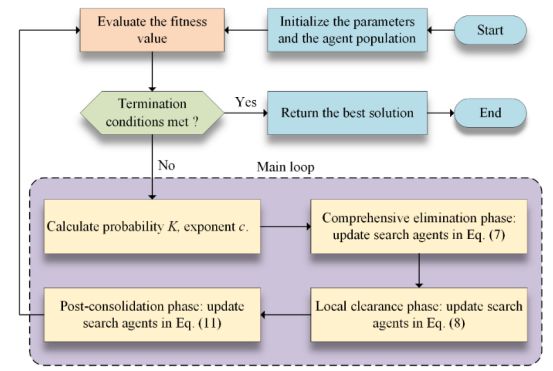
2.结果展示
在经典的23个函数集上进行测试:
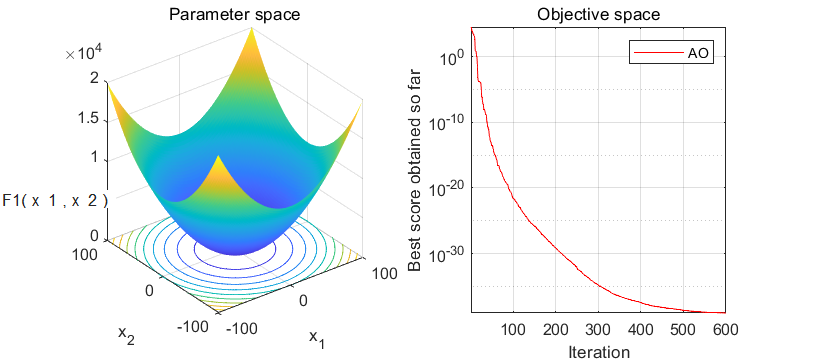
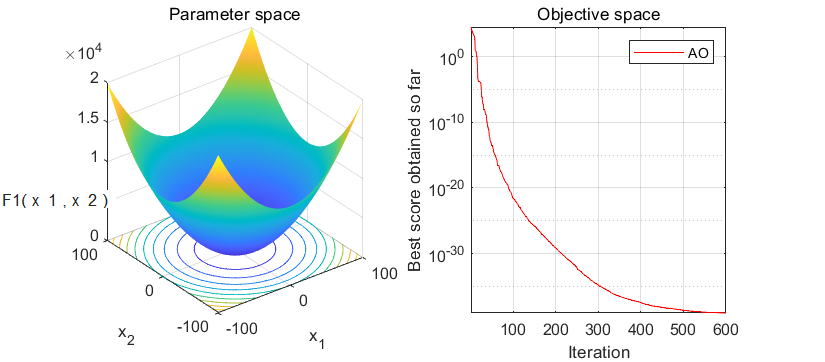
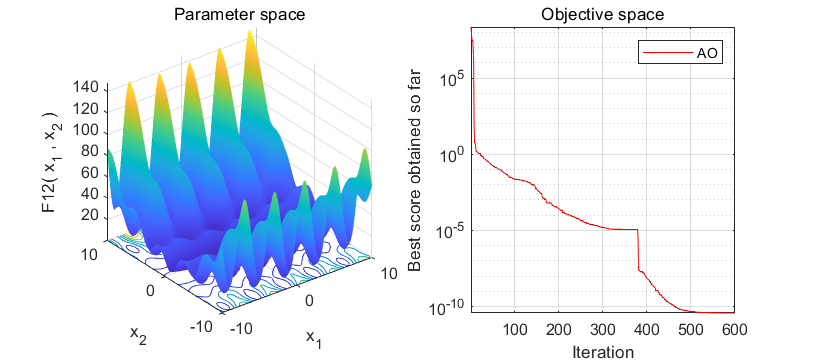
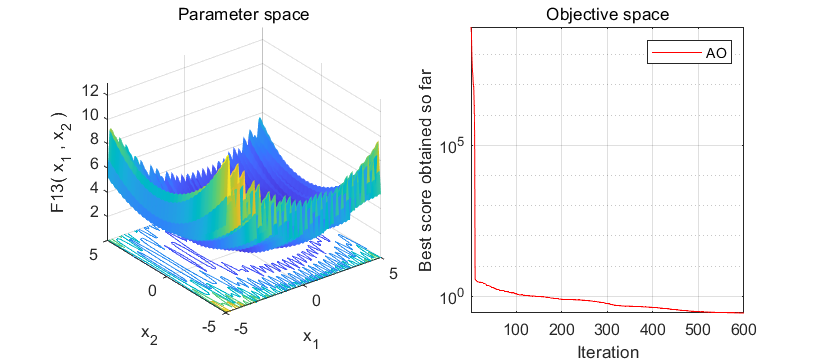
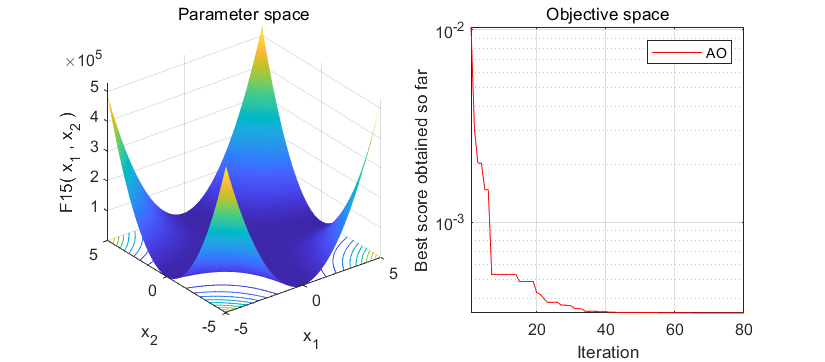
3.MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 青蒿素优化算法(AO)
function [Leader_pos,bestfitness,Convergence_curve]=AO(fobj,lb,ub,dim,N,MaxFEs)
% Initialization parameters
FEs=0;
it=1;
%% Initialization of the solution set
pop=initialization(N,dim,ub,lb);
%Calculate the fitness value of the initial solution set
for i=1:N
Fitness(i)=fobj(pop(i,:));
FEs=FEs+1;
end
[fmin,x]=min(Fitness);
%Container
New_pop=zeros(N,dim);
Fitnorm=zeros(1,N);
Convergence_curve=[];
%Record the current optimal solution
best=pop(x,:);
bestfitness=fmin;
%% Main loop
while FEs<=MaxFEs
K= 1-((FEs)^(1/6)/(MaxFEs)^(1/6));
E =1*exp(-4*(FEs/MaxFEs));
%
for i=1: N
Fitnorm(i)= (Fitness(i)-min(Fitness))/(max(Fitness)-min(Fitness));
for j=1:dim
if rand<K
if rand<0.5
New_pop(i,j) = pop(i,j)+E.*pop(i,j)*(-1)^FEs;
else
New_pop(i,j) = pop(i,j)+E.*best(j)*(-1)^FEs;
end
else
New_pop(i,j)=pop(i,j);
end
if rand<Fitnorm(i)
A=randperm(N);
beta=(rand/2)+0.1;
New_pop(i,j)=pop(A(3),j)+beta.*(pop(A(1),j)-pop(A(2),j));
end
end
New_pop(i,:)=Mutation(New_pop(i,:),pop(i,:),best,dim);
New_pop(i,:)=Transborder_reset(New_pop(i,:),ub,lb,dim,best);
tFitness=fobj(New_pop(i,:));
FEs=FEs+1;
if tFitness<Fitness(i)
pop(i,:)= New_pop(i,:);
Fitness(i)=tFitness;
end
end
[fmin,x]=min(Fitness);
if fmin<bestfitness
best=pop(x,:);
bestfitness=fmin;
end
Convergence_curve(it)=bestfitness;
Leader_pos=best;
it=it+1;
end
end
function z=Mutation(z,x,b,dim)
for j=1:dim
if rand<0.05
z(j)=x(j);
end
if rand<0.2
z(j)=b(j);
end
end
end
function z=Transborder_reset(z,ub,lb,dim,best)
for j=1:dim
if z(j)>ub || z(j)<lb
z(j)=best(j);
end
end
end
4.参考文献
Yuan C, Zhao D, Heidari A A, et al. Artemisinin optimization based on malaria therapy: Algorithm and applications to medical image segmentation[J]. Displays, 2024, 84: 102740.
完整代码获取
点击下方卡片,后台回复关键词:
TGDM839






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










