目录
剑指Offer(10)--斐波那契数列(青蛙跳台阶)
题目:
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
#include<iostream>
using namespace std;
//递归解法
long long Fibonacci1(unsigned int n)
{
if (n <= 0)
return 0;
if (n == 1)
return 1;
return Fibonacci1(n - 1) + Fibonacci1(n - 2);
}
//从下到上,避免重复计算
long long Fibonacci2(unsigned int n)
{
if (n == 0)
return 0;
if (n == 1)
return 1;
long long one = 1;
long long two = 0;
long long result = 0;
for (int i = 2; i <= n; ++i)
{
result = one + two;
two = one;
one = result;
}
return result;
}
剑指Offer(11)--旋转数组的最小数字
题目:
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
思路:
类似于二分查找,用两个指针分别指向数组的第一个元素和最后一个元素。然后找到中间元素,如果中间元素大于等于第一个指针所指元素,那么最小元素是在后面,所以将第一个指针移到中间元素位置,然后重复上面操作。如果中间元素小于第一个指针所指元素,那么最小元素应该是在前面,所以将最后一个指针移到中间元素,然后重复上面操作。
有一种特殊情况,如果第一个指针所指元素和最后一个指针所指元素还有中间元素的值都相同,那么需要依次遍历。因为不一定是在前面还是在后面。
#include<iostream>
using namespace std;
int Min(int *numbers, int length)
{
if (numbers == nullptr || length <= 0)
return -1;
int index1 = 0;
int index2 = length - 1;
//防止搬移的是0个元素
int mid = index1;
while (numbers[index1] >= numbers[index2])
{
//找到了
if (index2 - index1 == 1)
{
mid = index2;
break;
}
mid = (index1 + index2) / 2;
if (numbers[index1] == numbers[index2]
&& numbers[index1] == numbers[mid])
return MinInorder(numbers, index1, index2);
if (numbers[mid] >= numbers[index1])
index1 = mid;
else
index2 = mid;
}
return numbers[mid];
}
//针对的情况比如递增序列是:0,1,1,1,1
//两个不同的旋转1,1,1,0,1或者是1,0,1,1,1
int MinInorder(int *numbers, int index1, int index2)
{
int result = numbers[index1];
for (int i = index1 + 1; i <= index2; ++i)
{
if (result > numbers[i])
result = numbers[i];
}
return result;
}
剑指Offer(12)--矩阵中的路径
题目:
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。 例如在下面的3x4的矩阵中包含一条字符串"bcced"的路径(路径中的字母用斜体表示)。但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。

思路:
回溯法,能走的出去,匹配的字符数加一,然后沿着当前路继续走;如果走不下去了,返回来,同时要将匹配的字符数减一。
#include<iostream>
using namespace std;
bool hasPath(char *matrix, int rows, int cols, char *str)
{
if (matrix == nullptr || rows < 1 || cols < 1 || str == nullptr)
return false;
bool *visited = new bool[rows*cols];
/*
C++在new时的初始化的规律可能为:对于有构造函数的类,
不论有没有括号,都用构造函数进行初始化;如果没有构造函数,
则不加括号的new只分配内存空间,不进行内存的初始化,
而加了括号的new会在分配内存的同时初始化为0。
*/
memset(visited, 0, rows*cols);
int count = 0;
for (int i = 0; i < rows; ++i)
for (int j = 0; j < cols; ++j)
{
if (HasPathCore(matrix, rows, cols, i, j,
str, count, visited))
return true;
}
delete[]visited;
return false;
}
bool HasPathCore(const char *matrix, int rows, int cols, int row,
int col, const char *str, int &count, bool *visited)
{
if (str[count] == '\0')
return true;
bool hasPath = false;
if (row >= 0 && row < rows && col >= 0 && col < cols
&& matrix[row*cols + col] == str[count] && !visited[row*cols + col])
{
++count;
visited[row*cols + col] = true;
hasPath = HasPathCore(matrix, rows, cols, row, col - 1,
str, count, visited)
|| HasPathCore(matrix, rows, cols, row, col + 1,
str, count, visited)
|| HasPathCore(matrix, rows, cols, row - 1, col,
str, count, visited)
|| HasPathCore(matrix, rows, cols, row + 1, col,
str, count, visited);
if (!hasPath)
{
--count;
visited[row*cols + col] = false;
}
}
return hasPath;
}
int main(void)
{
bool *arr = new bool[3];
memset(arr, 0, 3);
cout << arr[1] << endl;
system("pause");
return 0;
}
剑指Offer(13)--机器人的运动范围
题目:
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
思路:
同上面那道题,回溯法解决,如果当前符合,一直走。只不过回退的时候结果不需要改变。
#include<iostream>
using namespace std;
int movingCount(int value, int rows, int cols)
{
if (rows < 1 || cols < 1 || value<=0)
return 0;
bool *visited = new bool[rows*cols];
memset(visited, 0, rows*cols);
int result = movingCountCore(value, rows, cols, 0, 0, visited);
return result;
}
int movingCountCore(int value, int rows, int cols, int row,
int col, bool *visited)
{
int count = 0;
//判断当前cow,col是否符合要求,如果符合,看它的前后左右
if (row >= 0 && row < rows && col >= 0 && col < cols &&
Sum(row) + Sum(col) <= value && !visited[row*cols + col])
{
visited[row*cols + col] = 1;
count = 1 + movingCountCore(count, rows, cols, row - 1, col, visited)
+ movingCountCore(count, rows, cols, row + 1, col, visited)
+ movingCountCore(count, rows, cols, row, col + 1, visited)
+ movingCountCore(count, rows, cols, row, col - 1, visited);
}
return count;
}
int Sum(int number)
{
int sum = 0;
while (number > 0)
{
sum += number % 10;
number /= 10;
}
return sum;
}
剑指Offer(14)--剪绳子
题目:
一根长度为n的绳子,剪成m段,m,n都大于1,且都为整数,每段长度记为k[0],k[1]…,k[m].求k[0]*k[1]…*k[m]可能的最大乘积。
思路:
利用动态规划进行解决,当绳子长度为n时,需要将之前的最优解记录在一个数组中。
#include<iostream>
using namespace std;
int MaxValue(int length)
{
if (length < 2)
return 0;
//最少都得?一刀
if (length == 2)
return 1;
if (length == 3)
return 2;
int *arr = new int[length + 1];
arr[0] = 0;
arr[1] = 1;
arr[2] = 2;
arr[3] = 3;
int result = 0;
for (int i = 4; i <= length; ++i)
{
int max = 0;
//到了i/2之后就可以了,再往后就重复了
for (int j = 1; j <= i / 2; ++j)
{
int cur = arr[j] * arr[i - j];
if (cur > max)
max = cur;
}
arr[i] = max;
}
result = arr[length];
delete[]arr;
return result;
}
int main(void)
{
cout << MaxValue(8) << endl;
system("pause");
return 0;
}剑指Offer(15)--二进制中1的个数
题目:
请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
思路一:
将整数的每一位与1进行与运算,具体实现就是将1左移。
#include<iostream>
using namespace std;
int NumberOf1(int n)
{
int count = 0;
int flag = 1;
//一共循环32次,第33次左移变为0,因为整数是32位
while (flag)
{
if (n&flag)
++count;
flag = flag << 1;
}
return count;
}思路二:
把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于把整数的二进制表示中最右边的1变为0。
#include<iostream>
using namespace std;
int NumberOf1(int n)
{
int count = 0;
while (n)
{
++count;
n = (n - 1)&n;
}
return count;
}剑指Offer(17)--打印从1到最大的n位数
题目:
输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,则输出1、2、3一直到最大的3位数即999。
思路:
题目并没有规定n的范围。当输入的n很大的时候,用整型int或者长整型long long都会溢出。
递归求解,先计算第一位,然后第二位,一直到第n位。
#include<iostream>
using namespace std;
void Print1ToMaxOfNDigitsCore(char *number, int length, int index);
//碰到第一个非0的字符之后才开始打印
void PrintNumber(char* number)
{
int length = strlen(number);
for (int i = 0; i < length; ++i)
{
if (number[i] != '0')
{
cout << number + i << endl;
return;
}
}
return;
}
void Print1ToMaxOfNDigits(int n)
{
if (n < 1)
return;
//多一位存放'\0'
char *number = new char[n + 1];
number[n] = '\0';
//第一位可以是0-9
for (int i = 0; i < 10; ++i)
{
number[0] = i + '0';
Print1ToMaxOfNDigitsCore(number, n, 0);
}
delete[]number;
}
//计算第二位、第三位等等
void Print1ToMaxOfNDigitsCore(char *number, int length, int index)
{
if (index == length - 1)
{
PrintNumber(number);
return;
}
for (int i = 0; i < 10; ++i)
{
number[index + 1] = i + '0';
Print1ToMaxOfNDigitsCore(number, length, index + 1);
}
}
int main(void)
{
Print1ToMaxOfNDigits(3);
system("pause");
return 0;
}
剑指Offer(47)--礼物的最大价值
题目:
在一个 m*n 的棋盘中的每一个格都放一个礼物,每个礼物都有一定的价值(价值大于0).你可以从棋盘的左上角开始拿各种里的礼物,并每次向左或者向下移动一格,直到到达棋盘的右下角。给定一个棋盘及上面个的礼物,请计算你最多能拿走多少价值的礼物?
比如说现在有一个如下的棋盘,

在这个棋盘中,按照(1,12,5,7,7,16,5)的顺序可以拿到总价值最大的礼物。
思路:
动态规划进行求解
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int GetMaxValue(const vector<vector<int>>& data)
{
if (data.size() == 0)
return 0;
int rows = data.size();
int cols = data[0].size();
vector<vector<int>> v(rows, vector<int>(cols, 0));
for (int i = 0; i < rows; ++i)
{
for (int j = 0; j < cols; ++j)
{
int left = 0;
int up = 0;
if (i > 0)
up = v[i - 1][j];
if (j > 0)
left = v[i][j - 1];
v[i][j] = max(left, up) + data[i][j];
}
}
return v[rows - 1][cols - 1];
}
int main(void)
{
vector<vector<int>> data{ {1,10,3,8},{12,2,9,6},{5,7,4,11},{3,7,16,5} };
cout << GetMaxValue(data) << endl;
system("pause");
return 0;
}
 剑指Offer:递归与循环解题策略
剑指Offer:递归与循环解题策略





 本文介绍了《剑指Offer》中涉及递归、循环和位运算的解题方法,包括斐波那契数列、旋转数组最小数字、矩阵路径、机器人运动范围、剪绳子、二进制中1的个数、打印n位数以及最大礼物价值问题,通过递归、动态规划和回溯等算法进行解析。
本文介绍了《剑指Offer》中涉及递归、循环和位运算的解题方法,包括斐波那契数列、旋转数组最小数字、矩阵路径、机器人运动范围、剪绳子、二进制中1的个数、打印n位数以及最大礼物价值问题,通过递归、动态规划和回溯等算法进行解析。
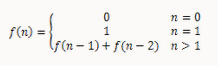
















 3795
3795

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








