Codefoces Round 981(D-F)

https://codeforces.com/contest/2033

D 

思路：判断一段数和为0，可推出其中会有两个和是出现两次的，即此段数和之前和此段数和之后，我们用一个map来记录就行，因为此段数不能重叠，所以我们在每找到一段时，要把之前的记录删除就可以了；特别得，考虑开始前几个和就为0，例如：3 -1 -2，但map[0]没有记录，所以加一个sum=0就可以，也可以一开始设置map[0] = 1,但在每次清空map时还要加上map[0]=1,繁琐不推荐。代码如下：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define endl '\n'
#define fo(i,l,r) for(int i=(l);i<=(r);++i)

void solve()
{
    int n;
    cin >> n;
    vi a(n);
    map<int, int> pre; 
    int sum = 0;
    int res = 0;
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
        sum += a[i];
        if (sum == 0 || pre[sum] > 0) {
            res++; 
            sum = 0;
            pre.clear(); 
        }
        pre[sum]++;
    }
    cout << res << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    int t = 1; 
    cin >> t;
    while (t--)
    {
        solve();
    }
    
    return 0;
}

E

思路：当和不需要考虑，然后把其他点对应相连，形成环观察，当交换一对数字时假设缺口处自动连到合并，以样例三为例，如图所示：

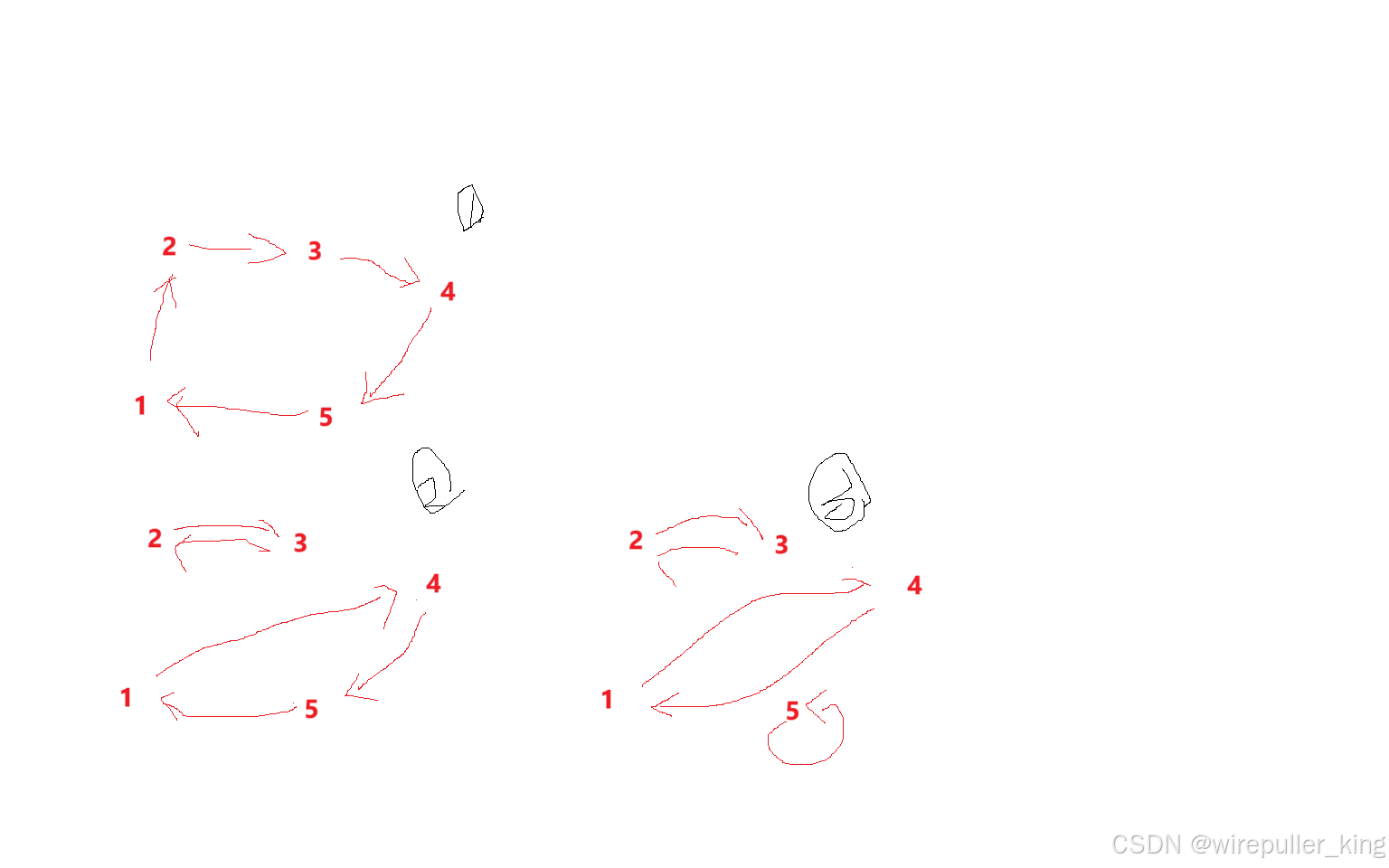
即可推出公式处理每个环的个数：（n-1）/2,累计相加即可。代码如下：

#include <bits/stdc++.h>
#include<array>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define endl '\n'
void solve()
{
    ll n;
    cin >> n;
    vector<ll>a(n + 1);
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
    }
    vector<int>vis(n + 1);
    ll ans = 0;
    for (int i = 1; i <= n; ++i)
    {
        int cnt = 0;
        if (!vis[a[i]])
        {
            int now = a[i];
            while (!vis[now])
            {
                cnt++;
                vis[now] = 1;
                now = a[now];
            }
            ans += (cnt - 1) / 2;
        }
    }
    cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int t = 1;
    cin >> t;
    for (int i = 1; i <= t; i++)
    {
        solve();
    }

    return 0;
}

F

思路：找规律很好找，主要理解如何推出这个公式的

假设当k=3时，数列为

1

1

2

3

5

8

13

21

34

化为模k后的结果：

1

1

2

0

2

2

1

0

...

这样已经能看出规律了，再直观一点当k不定时为

...

...

a

0

a

a

...

...

...

 在0后的两个数相同，可以想象相约为1，1这不是又从头开始了吗，及两个模k为0的数的间距相等，所以只要找到第一个模k为0的所以再乘上个数就可以了，代码如下：

#include <bits/stdc++.h>
#include<array>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define endl '\n'
const int mod = 1e9 + 7;
void solve()
{
    ll n, k;
    cin >> n >> k;
    if (k == 1)
    {
        cout << n % mod << endl;
        return;
    }
    if (k == 2)
    {
        cout << n % mod * 3 % mod << endl;
        return;
    }
    ll num = 2;
    ll p1 = 1, p2 = 1, p3 = 2;
    while (p3!=0)
    {
        p3 = (p1 + p2) % k;
        p1 = p2;
        p2 = p3;
        num++;
    }
    cout << num % mod * (n % mod) % mod << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    int t = 1;
    cin >> t;
    for (int i = 1; i <= t; i++)
    {
        solve();
    }
    return 0;
}

如有误请评论指出