基础知识:
条件概率:P(A∣B)=P(AB)P(B)P(A|B)=\frac{P(AB)}{P(B)}P(A∣B)=P(B)P(AB)
乘法定理:P(AB)=P(A∣B)P(B)=P(B∣A)P(A)P(AB)=P(A|B)P(B)=P(B|A)P(A)P(AB)=P(A∣B)P(B)=P(B∣A)P(A)
全概公式:B1∪B1∪...Bn=Ω,且Bi∩Bj=空集,则P(A)=∑i=1nP(A∣Bi)P(Bi)B_{1}\cup B_{1}\cup ...B_{n}=\Omega,且B_{i}\cap B_{j}=空集,则P(A)=\sum_{i=1}^{n}P(A|B_{i})P(B_{i})B1∪B1∪...Bn=Ω,且Bi∩Bj=空集,则P(A)=∑i=1nP(A∣Bi)P(Bi)
贝叶斯公式:P(Bi∣A)=P(A∣Bi)P(Bi)∑j=1nP(A∣Bj)P(Bj)P(B_{i}|A)=\frac{P(A|B_{i})P(B_{i})}{\sum_{j=1}^{n}P(A|B_{j})P(B_{j})}P(Bi∣A)=∑j=1nP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
贝叶斯决策论
贝叶斯决策论(Bayesian decision theory)是概率框架下进行决策的基本方法。对于分类任务,所有相关概率都已知的理想情况下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
最大后验概率贝叶斯决策:
基于观察特征,类别的贝叶斯公式:
P(ωi∣x)=likelihood×priorevidence=P(x∣ωi)P(ωi)P(x)=P(x∣ωi)P(ωi)∑j=1nP(x∣ωj)P(ωj)P(\omega_{i}|x)=\frac{likelihood\times prior}{evidence}=\frac{P(x|\omega_{i})P(\omega_{i})}{P(x)}=\frac{P(x|\omega_{i})P(\omega_{i})}{\sum_{j=1}^{n}P(x|\omega_{j})P(\omega_{j})}P(ωi∣x)=evidencelikelihood×prior=P(x)P(x∣ωi)P(ωi)=∑j=1nP(x∣ωj)P(ωj)P(x∣ωi)P(ωi)
其中ωi\omega_{i}ωi为类别,xxx为样本。P(x)P(x)P(x)为在数据集D中出现的概率,属于一个依据(evidence);P(ωi)P(\omega_{i})P(ωi)为数据集中出现该类别的概率,属于先验概率(prior);P(x∣ωi)P(x|\omega_{i})P(x∣ωi)属于似然函数(likehood)。所求的P(ωi∣x)P(\omega_{i}|x)P(ωi∣x)为后验概率(posterior)。
因为对于给定的样本xxx,所有类别的P(x)P(x)P(x)都相同,所以:
P(ωi∣x)∝P(x∣ωi)P(ωi)P(\omega_{i}|x)\propto P(x|\omega_{i})P(\omega_{i})P(ωi∣x)∝P(x∣ωi)P(ωi)
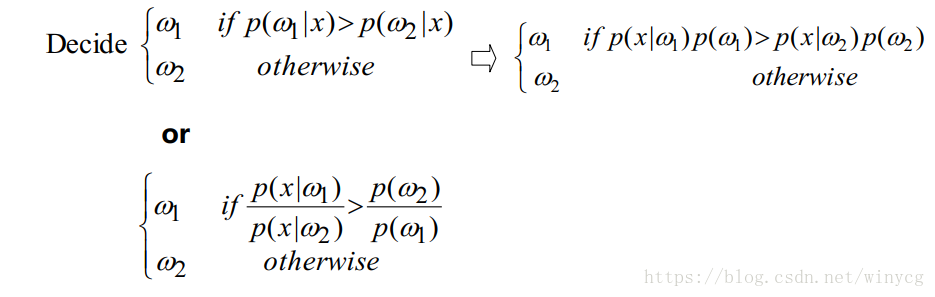
概率函数:有3种形式
gi(x)=P(ωi∣x)∝P(x∣ωi)P(ωi)∝lnP(x∣ωi)+lnP(ωi)g_{i}(x)=P(\omega_{i}|x)\propto P(x|\omega_{i})P(\omega_{i})\propto \ln P(x|\omega_{i})+\ln P(\omega_{i})gi(x)=P(ωi∣x)∝P(x∣ωi)P(ωi)∝lnP(x∣ωi)+lnP(ωi)
最优决策,也称为最小错误率贝叶斯决策:ω∗=maxω∈YP(ω∣x)=maxω∈Y[lnP(x∣ω)+lnP(ω)]\omega^{*}=\max_{\omega\in \mathcal{Y}}P(\omega|x)=\max_{\omega\in \mathcal{Y}}[\ln P(x|\omega)+\ln P(\omega)]ω∗=ω∈YmaxP(ω∣x)=ω∈Ymax[lnP(x∣ω)+lnP(ω)]
最小风险贝叶斯决策:
设有KKK种可能的标记,Y={ω1,...,ωK}\mathcal{Y}=\{\omega_{1},...,\omega_{K}\}Y={ω1,...,ωK},λij\lambda_{ij}λij是将真实标记为ωj\omega_{j}ωj的样本误分类为ωi\omega_{i}ωi所产生的的损失。基于后验概率P(ω∣x)P(\omega|\bm{x})P(ω∣x)可获得将样本x\bm{x}x分类为的ωi\omega_{i}ωi的期望损失,即在样本x\bm{x}x的条件风险(决策论中将期望损失称为风险)
R(ωi∣x)=∑j=1KλijP(ωj∣x)R(\omega_{i}|\bm{x})=\sum_{j=1}^{K}\lambda_{ij}P(\omega_{j}|\bm{x})R(ωi∣x)=j=1∑KλijP(ωj∣x)
通过最小化风险进行决策:
ω∗=argminω∈YR(ω∣x)\omega^{*}=\arg \min_{\omega\in \mathcal{Y}}{R(\omega|\bm{x})}ω∗=argω∈YminR(ω∣x)
若λij={0, if i=j1, otherwise\lambda_{ij}=\left\{\begin{matrix}
0,\ if\ i=j\\
1,\ otherwise
\end{matrix}\right.λij={0, if i=j1, otherwise
此时条件风险为:
R(ω∣x)=1−P(c∣x)R(\omega|\bm{x})=1-P(c|\bm{x})R(ω∣x)=1−P(c∣x)此时最小风险贝叶斯决策就变为最小分类错误率的贝叶斯决策:
ω∗=maxω∈YP(ω∣x)\omega^{*}=\max_{\omega\in \mathcal{Y}}P(\omega|x)ω∗=ω∈YmaxP(ω∣x)
总结
最小化决策风险首先要获得后验概率P(ω∣x)P(\omega|\bm{x})P(ω∣x),现实任务中通常很难获得,从这个角度说,机器学习的方法所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率P(ω∣x)P(\omega|\bm{x})P(ω∣x)。从计算后验概率P(ω∣x)P(\omega|\bm{x})P(ω∣x)的策略上来说,可以分为判别式模型(discriminative models)和生成式模型(generative models)。前者为给定样本x\bm{x}x,直接建模P(ω∣x)P(\omega|\bm{x})P(ω∣x)来预测类别,例如决策树,BP神经网络和SVM;后者为给定样本x\bm{x}x,建模联合概率分布P(x∣ω)P(\bm{x}|\omega)P(x∣ω),然后再得到P(ω∣x)P(\omega|\bm{x})P(ω∣x),例如朴素贝叶斯分类器。
对于生成式模型来说,必然考虑:
P(ω∣x)=P(x∣ω)P(ω)P(x)P(\omega|\bm{x})=\frac{P(\bm{x}|\omega)P(\omega)}{P(\bm{x})}P(ω∣x)=P(x)P(x∣ω)P(ω)
对P(x∣ω)P(\bm{x}|\omega)P(x∣ω)来说,涉及到关于x\bm{x}x的所有属性的联合概率,直接根据样本出现的频率来估计将会遇到严重的困难。例如,假设样本有ddd个属性都是二值的,则样本空间有2d2^{d}2d中可能的取值,现实应用中这个值远大于训练样本mmm个,等价于说很多样本取值的在训练集中没有出现,所以直接使用频率来估计P(x∣ω)P(\bm{x}|\omega)P(x∣ω)在实际应用中是不可行的。
贝叶斯分类器
朴素贝叶斯分类器
从上述的总结可知,直接根据有限训练集中出现的样本频率去估计联合概率是行不通的。为了解决这个问题,朴素贝叶斯采用了属性条件独立性假设,即假设P(x∣c)P(\bm{x}|c)P(x∣c)中x\bm{x}x特征向量的各维属性相互独立,一共ddd个属性
P(c∣x)=P(c)P(x∣c)P(x)∝P(c)P(x∣c)=P(c)∏i=1dP(xi∣c)P(c|\bm{x})=\frac{P(c)P(\bm{x}|c)}{P(\bm{x})} \propto P(c)P(\bm{x}|c)=P(c)\prod_{i=1}^{d}P(x_{i}|c)P(c∣x)=P(x)P(c)P(x∣c)∝P(c)P(x∣c)=P(c)i=1∏dP(xi∣c)
决策:
h(x)=argmaxc∈Cp(c)∏i=1dP(xi∣c)h(\bm{x})=\arg \max_{c \in C}p(c)\prod_{i=1}^{d}P(x_{i}|c)h(x)=argc∈Cmaxp(c)i=1∏dP(xi∣c)
上式就是朴素贝叶斯分类器的表达式。
朴素贝叶斯分类器的训练过程就是基于训练集DDD确定类别先验概率p(c)p(c)p(c)和每个属性估计条件条件概率P(xi∣c)P(x_{i}|c)P(xi∣c)。对于每一个测试样本x\bm{x}x,带入h(x)h(\bm{x})h(x),根据从训练集确定好的p(c)p(c)p(c)和p(xi∣c)p(x_{i}|c)p(xi∣c)从而可以算出h(x)h(\bm{x})h(x)。
(1)类别先验概率:P(c)=∣Dc∣∣D∣P(c)=\frac{|D_{c}|}{|D|}P(c)=∣D∣∣Dc∣
(2)属性的条件概率:
xix_{i}xi离散情况:
P(xi∣c)=∣Dc,xi∣∣Dc∣P(x_{i}|c)=\frac{|D_{c,x_{i}}|}{|D_{c}|}P(xi∣c)=∣Dc∣∣Dc,xi∣
其中Dc,xiD_{c,x_{i}}Dc,xi表示在DcD_{c}Dc中第iii个属性上取值为xix_{i}xi的样本组成的集合。
xix_{i}xi连续情况,就要考虑概率密度函数。可以假定P(xi∣c)∼N(μc,i,c,i)P(x_{i}|c) \sim \mathcal{N}(\mu_{c,i},c,i)P(xi∣c)∼N(μc,i,c,i):P(xi∣c)=12πσc,iexp(−(xi−μc,i)22σc,i2)P(x_{i}|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}\exp ({-\frac{(x_{i}-\mu_{c,i})^{2}}{2\sigma^{2}_{c,i}}})P(xi∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)
其中,这表示特征xix_{i}xi与表现为类别ccc的概率满足正态分布,μc,i\mu_{c,i}μc,i和σc,i2\sigma^{2}_{c,i}σc,i2为类别ccc的样本在iii属性上的取值的均值和标准差。
拉普拉斯修正:
当测试样本中出现训练集没有出现过的属性xix_{i}xi时,P(xi∣c)=0P(x_{i}|c)=0P(xi∣c)=0,此时连乘式得到的结果会0。此时需要进行概率值的平滑,给予P(xi∣c)P(x_{i}|c)P(xi∣c)一个较小的概率值。
P^(c)=∣Dc∣+1∣D∣+NP^(xi∣c)=∣Dc,xi∣+1∣Dc∣+Ni\hat{P}(c)=\frac{|D_{c}|+1}{|D|+N} \\
\hat{P}(x_{i}|c)=\frac{|D_{c,x_{i}}|+1}{|D_{c}|+N_{i}}P^(c)=∣D∣+N∣Dc∣+1P^(xi∣c)=∣Dc∣+Ni∣Dc,xi∣+1
拉普拉斯修正避免了因训练集样本不充分而导致的概率值为0的问题,该修正实质上假设了属性值与类别均匀分布,这相当于额外引入的先验。在数据集变大时,修正的影响可以可以被忽略,使得估值趋向于实际概率值。
现实任务中,朴素贝叶斯分类器有多种使用方式。若任务对预测速度要求较高,则给定训练集,将分类器涉及到的所有概率估值事先存储,预测时只需要查表可进行判别;若任务更换频繁,可采用惰性学习的方法,先不进行任何训练,等收到预测请求时再根据数据集进行概率估值。
正态密度的贝叶斯分类器
h(x)=argmaxc∈Cp(c)p(x∣c)h(x)=\arg \max_{c \in C}p(c)p(x|c)h(x)=argmaxc∈Cp(c)p(x∣c)中的p(x∣c)p(x|c)p(x∣c)满足正态分布。
正态分布:p(x)=12πσexp(−(x−μ)22σ2)p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})p(x)=2πσ1exp(−2σ2(x−μ)2)
均值μ=ε[x]=∫−∞∞xp(x)dx\mu=\varepsilon[x]=\int_{-\infty}^{\infty}xp(x)dxμ=ε[x]=∫−∞∞xp(x)dx
方差σ2=ε[(x−μ)2]=∫−∞∞(x−μ)2p(x)dx\sigma^{2}=\varepsilon[(x-\mu)^{2}]=\int_{-\infty}^{\infty}(x-\mu)^{2}p(x)dxσ2=ε[(x−μ)2]=∫−∞∞(x−μ)2p(x)dx
多元正态分布概率密度函数:
p(x)∼N(μ,Σ),x=[x1,x2,...,xd]Tp( \rm{x})\sim N(\mu, \Sigma),x=[x_{1},x_{2},...,x_{d}]^{T}p(x)∼N(μ,Σ),x=[x1,x2,...,xd]T
p(x)=1(2π)d/2∣Σ∣1/2exp[−12(x−μ)TΣ−1(x−μ)]p( \rm{x})=\frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}}\exp[-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)]p(x)=(2π)d/2∣Σ∣1/21exp[−21(x−μ)TΣ−1(x−μ)]
Mean:μ=ε[x]=∫xp(x)dx, μi=ε[xi]{\rm{Mean:}}\mu=\varepsilon[ {\rm{x}}]=\int {\rm{x}}p({\rm{x}})d{\rm{x}},\ \mu_{i}=\varepsilon[x_{i}] Mean:μ=ε[x]=∫xp(x)dx, μi=ε[xi]
Covariance Matrix:Σ=ε[(x−μ)(x−μ)T]=∫(x−μ)(x−μ)Tdx=[σ11σ12⋯σ1dσ21σ22⋯σ2d⋮⋮⋱⋮σd1σd2⋯σdd]{\rm{Covariance\ Matrix:}}\Sigma=\varepsilon[({\rm{x}}-\mu)({\rm{x}}-\mu)^{T}]=\int({\rm{x}}-\mu)({\rm{x}}-\mu)^{T}d{\rm{x}}\\
=\begin{bmatrix}
\sigma_{11} & \sigma_{12} & \cdots & \sigma_{1d}\\
\sigma_{21} & \sigma_{22} & \cdots & \sigma_{2d} \\
\vdots&\vdots&\ddots&\vdots \\
\sigma_{d1} & \sigma_{d2} & \cdots & \sigma_{dd} \\
\end{bmatrix}Covariance Matrix:Σ=ε[(x−μ)(x−μ)T]=∫(x−μ)(x−μ)Tdx=⎣⎢⎢⎢⎡σ11σ21⋮σd1σ12σ22⋮σd2⋯⋯⋱⋯σ1dσ2d⋮σdd⎦⎥⎥⎥⎤
σij=ε[(xi−μi)(xj−μj)]\sigma_{ij}=\varepsilon[(x_{i}-\mu_{i})(x_{j}-\mu_{j})]σij=ε[(xi−μi)(xj−μj)],如果xix_{i}xi与xjx_{j}xj相互独立,那么σij=0\sigma_{ij}=0σij=0
高斯密度下的判别函数
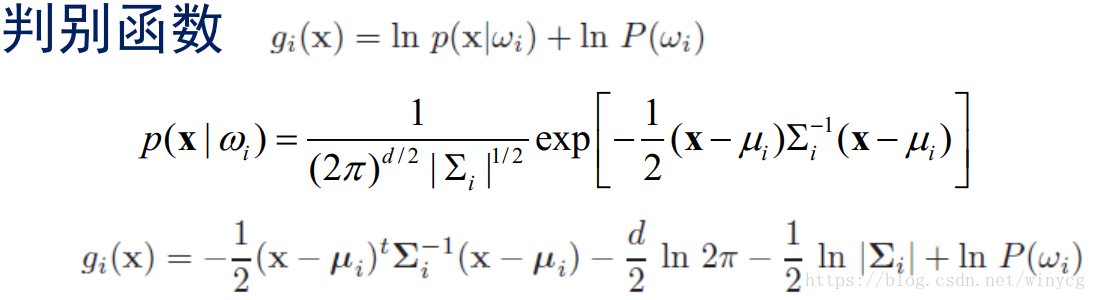
在不同协方差下的形式:
Case1: Σ=σ2I\Sigma=\sigma^{2}IΣ=σ2I
表示各xi,i=1,2,...,dx_{i},i=1,2,...,dxi,i=1,2,...,d之间相互独立,且具有相同的正态分布方差σ2\sigma^{2}σ2。此时可得:gi(x)=−∥x−μi∥2σ2+lnP(ωi)g_{i}({\rm{x}})=-\frac{\parallel {\rm{x}-\mu_{i}}\parallel }{2\sigma^{2}}+\ln P(\omega_{i})gi(x)=−2σ2∥x−μi∥+lnP(ωi)
gi(x)=−12σ2[xTx−2μiTx+μiTμi]+lnP(ωi)g_{i}({\rm{x}})=-\frac{1}{2\sigma^{2}}[{\rm{x}}^{T}{\rm{x}}-2\mu_{i}^{T}{\rm{x}}+\mu_{i}^{T}\mu_{i}]+\ln P(\omega_{i})gi(x)=−2σ21[xTx−2μiTx+μiTμi]+lnP(ωi)
抛除与类别无关的项xTx2σ2\frac{{\rm{x}}^{T}{\rm{x}}}{2\sigma^{2}}2σ2xTx,因为这一项每个g1,2,...,kg_{1,2,...,k}g1,2,...,k个函数中相同。化简得:
gi(x)=wiTx+wi0, wi=μiTσ2, wi0=−12σ2μiTμi+lnP(ωi)g_{i}({\rm{x}})={\rm{w_{i}^T}}{\rm{x}}+w_{i0},\ {\rm{w_{i}}}=\frac{\mu_{i}^{T}}{\sigma^{2}}, \ w_{i0}=-\frac{1}{2\sigma^{2}}\mu_{i}^{T}\mu_{i}+\ln P(\omega_{i})gi(x)=wiTx+wi0, wi=σ2μiT, wi0=−2σ21μiTμi+lnP(ωi)
二类决策面(判别函数相等的点构成):gi(x)−gj(x)=0g_{i}({\rm{x}})-g_{j}({\rm{x}})=0gi(x)−gj(x)=0即:

此时向量w{\rm{w}}w(连接两个圆心的向量)与法向量平面垂直。
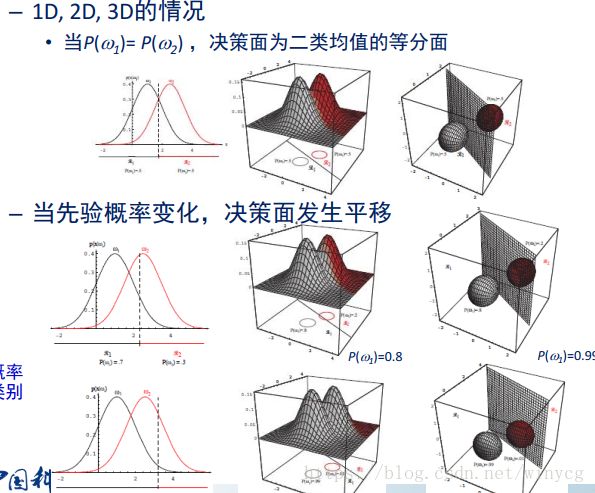
当类别先验概率相等时,退化为最小距离分类器。此时有:
w=μi−μj{\rm{w}}=\mu_{i}-\mu_{j}w=μi−μj
x0=12(μi+μj)\rm{x_{0}}=\frac{1}{2}(\mu_{i}+\mu_{j})x0=21(μi+μj)
如下所示:两个圆球表示样本的分布,圆心附近为样本的密集出,也就是μ\muμ,所有在分割面上的样本具有相同的概率值。
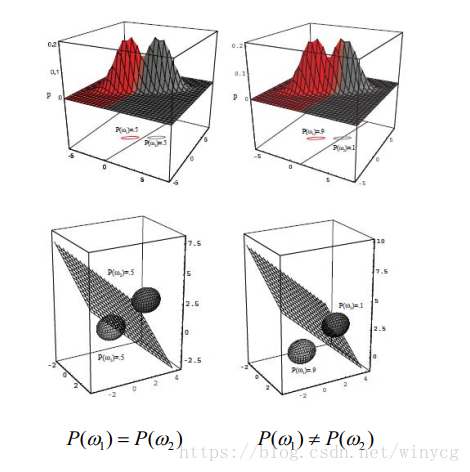
Case2:Σi=Σ\Sigma_{i}=\SigmaΣi=Σ
是指x{\rm{x}}x对所有类别的协方差矩阵都相等。

Case3: Σi=arbitrary\Sigma_{i}=arbitraryΣi=arbitrary,此时除以上两种情况外的情况
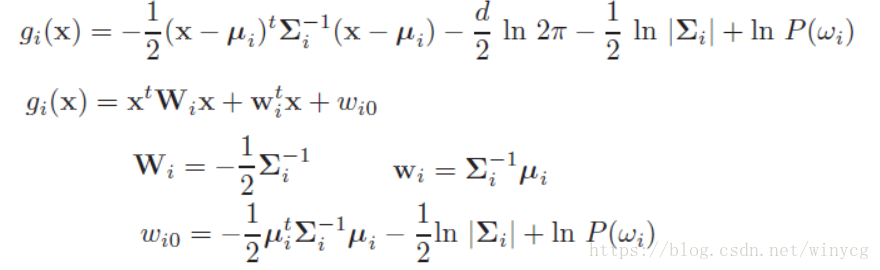
决策面比较复杂,gi(x)=gj(x)g_{i}({\rm{x}})=g_{j}(\rm{x})gi(x)=gj(x),可能为非线性。






 本文深入探讨贝叶斯决策理论,包括条件概率、全概率公式及贝叶斯公式,并详细解析最大后验概率贝叶斯决策。文章还介绍了朴素贝叶斯分类器及其训练过程,以及正态密度下的贝叶斯分类器。
本文深入探讨贝叶斯决策理论,包括条件概率、全概率公式及贝叶斯公式,并详细解析最大后验概率贝叶斯决策。文章还介绍了朴素贝叶斯分类器及其训练过程,以及正态密度下的贝叶斯分类器。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








