集成学习

集成方法（Ensemable method） 的目标是：将不同的分类器组成一个元分类器，与但个分类器相比，元分类器具有更好的泛化性能。通常使用多数投票的原则，将大多数分类器预测的结果作为最终的类标，即$$\hat{y}=mode(C_1(x),C_2(x),\cdots ,C_m(x)),mode为众数$$
对于二类别分类器来说，设正类为1，负类为-1，则预测结果可以表示为$$\hat{y}=sign[\sum _{i=1}^m{C}_i(x)]=\{\begin{array}{c}1,if{\sum }_{i=1}^m{C}_i(x)\ge 0\\ -1,other\end{array}$$

$C_1(x),C_2(x),\cdots ,C_m(x)$为训练后的$m$个分类器，分类器可以继承不同的分类算法，如决策树，支持向量机，逻辑斯谛回归等；还可以使用相同的分类算法使用拟合不同的训练子集。

证明集成分类器的性能好于单个成员分类器
假定二类别分类中的$n$个成员都有相同的错误率$\epsilon$，且分类器之间相互独立。此时分类器集成后出错的概率服从二项分布，设出错的分类器数量为$\lceil \frac{n}{2}\rceil$时集成分类器为错误（此时集成分类器不一定出错，但是可能会出错），所以： P { n u m E R R O R ≥ ⌈ n 2 ⌉ } = ∑ j = ⌈ n 2 ⌉ n ( n j ) ( ε ) j ( 1 − ε ) n − j P\{num_{ERROR}\geq\left \lceil \frac{n}{2} \right \rceil\}=\sum_{j=\left \lceil \frac{n}{2} \right \rceil}^n \binom{n}{j}(\varepsilon)^{j}(1-\varepsilon)^{n-j} P{numERROR​≥⌈2n​⌉}=j=⌈2n​⌉∑n​(jn​)(ε)j(1−ε)n−j
假定有11个分类器，单个分类器错误率为0.25，则集成后的错误率为:$${\epsilon }_{ensemble}=\sum _{j=6}^{11}\left(\genfrac{}{}{0ex}{}{11}{j}\right)(0.25{)}^j(1-0.25{)}^{11-j}=0.034$$

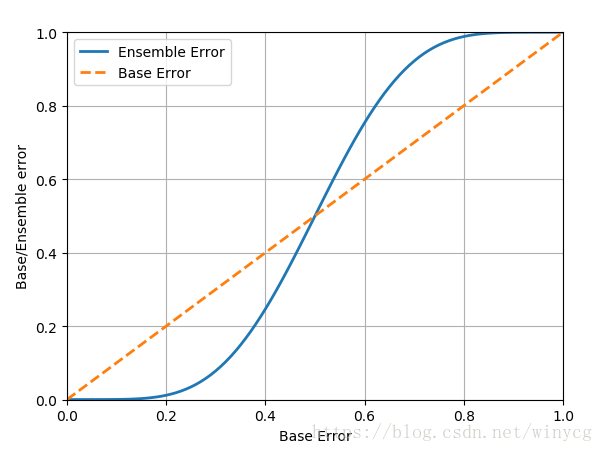
以下展示了11个分类器的情况下，成员分类器错误率与集成错误率的关系曲线。交点处大约为0.5。即在11个分类器的情况下，当成员分类器错误率<0.5时，集成分类器的错误率要低于成员分类率；当成员分类器错误率>0.5时，集成分类器的错误率要高于成员分类率

from scipy.misc import comb
import math
import numpy as np
import matplotlib.pyplot as plt


def ensemable_error(n_classifier, singal_error):
    probs = [comb(n_classifier, i) * 
             (singal_error ** i) * ((1-singal_error)**(n_classifier-i))
             for i in range(math.ceil(n_classifier / 2), n_classifier+1)]
    return sum(probs)


print(ensemable_error(8, 0.5))
error_range = np.arange(0.0, 1.01, 0.01)
ens_errors = [ensemable_error(11, error) for error in error_range]
plt.plot(error_range, ens_errors, label='Ensemble Error', linewidth=2)
plt.plot(error_range, error_range, label='Base Error', linewidth=2, linestyle='--')
plt.xlabel('Base Error')
plt.ylabel('Base/Ensemble error')
plt.legend(loc='best')
plt.xlim((0, 1))
plt.ylim((0, 1))
plt.grid()
plt.show()

目前的集成学习大致分为两种：
（1）个体学习器间存在强依赖关系，必须串行生成序列化方法，代表是Boosting算法：https://blog.youkuaiyun.com/winycg/article/details/82846802
（2）个体学习器之间不存在强依赖关系，可同时生成的并行化方法。代表是Bagging和随机森林：https://blog.youkuaiyun.com/winycg/article/details/82763334