目录
7.8 二叉树的下一个节点
7.9 对称的二叉树
7.10 按之字形顺序打印二叉树
7.11 把二叉树打印成多行
7.12 序列化二叉树
7.13 二叉搜索树的第k个结点
7.14 滑动窗口的最大值
7.15 机器人的运动范围
7.16 剪绳子
注:牛客网有对应的算法题目
第2章 面试需要的基础知识
这一题一看到是有序的数组立刻想到二分法查找,后来才发现直接套用一维的二分法便会在while循环中跳不出来,但如果直接遍历数组时间复杂度为O(n^2)。这里需要考虑题目中给出的数字已经有序了
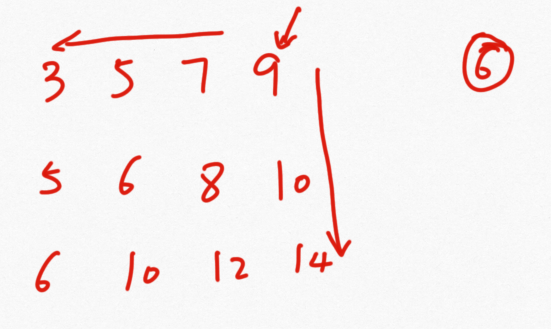
从右上角开始查询,根据目标值的大小来决定向哪个方向考量,这样可以减少遍历的数目,时间复杂的为O(N+M)。其实从右上角还是左下角移动的效果是一样的
public boolean Find(int target, int [][] array) {
int row = 0,col = array[0].length-1;
return find(array,0,col,target);
}
private boolean find(int[][] array, int row, int col,int target) {
if (row >= array.length || col < 0){
return false;
}
if (array[row][col] == target){
return true;
}else if (array[row][col] > target){
return find(array,row,col-1,target);
}else {
return find(array,row+1,col,target);
}
}
非递归写法如下:
public boolean Find(int target, int [][] array) {
int row = 0,col = array[0].length-1;
while (row < array.length && col > 0){
if (array[row][col] == target){
return true;
}else if (array[row][col] > target){
col = col-1;
}else {
row = row+1;
}
}
return false;
}
public String replaceSpace(StringBuffer str) {
StringBuffer stringBuffer = new StringBuffer();
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i)==' '){
stringBuffer.append("%20");
}else {
stringBuffer.append(str.charAt(i));
}
}
return stringBuffer.toString();
}
上面是自己写的代码,可以看到额外开辟了一个空间,那么能否不使用额外的空间那,如果直接使用Java的replace方法是可以直接在原字符串上进行修改的。
return str.toString().replaceAll(" " , "%20");
在这里可以认为自己写一个Java的replaceAll方法,且不使用额外的存储空间,算法的时间复杂度还有足够好。如果不适用额外的存储空间那么使用从前向后的顺序替换字符串如下图所示:
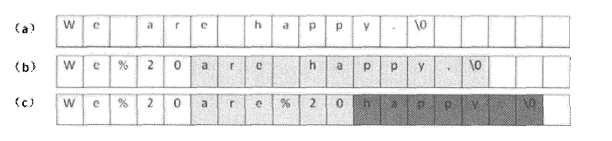
这样前面没替换一次后面的字符顺序就要改变一次,需要两层循环一层遍历空格一层修改遇到空格后后面的字符,那么时间复杂度为O(n^2)那么是否可以使用降低时间复杂度。这里效率的底下主要是因为前面的修改影响了后面,如果修改不会影响维修改的字符那么时间复杂度就会立刻下降,这里使用从后向前的遍历方式:
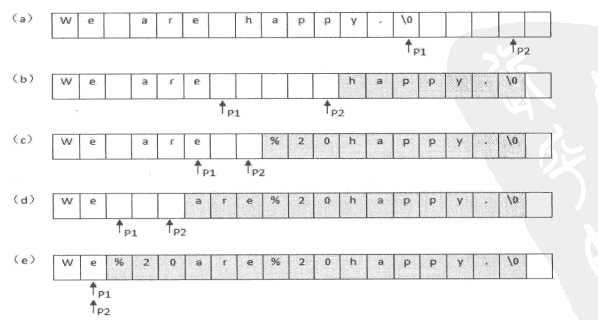
先计算出把空格修改后的新字符串的长度,再从后向前进行遍历修改即可。
public class Solution {
public String replaceSpace(StringBuffer str) {
if (str == null){
return null;
}
// 计算空格数
int spaceNum =0;
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == ' '){
spaceNum++;
}
}
// 替换前字符串的下标
int indexOld = str.length() - 1;
// 替换后字符串的长度
int newLength = str.length() + spaceNum*2;
// 替换后新的字符串的下标
int indexNew = newLength - 1;
// 设定新的字符串长度
str.setLength(newLength);
// 进行遍历修改,indexOld < newLength这个条件可以不用要的,这里只是为了防止意外情况
for (;indexOld >= 0 && indexOld < newLength; indexOld--){
if (str.charAt(indexOld) == ' '){
// 遇到空格便进行替换
str.setCharAt(indexNew--,'0');
str.setCharAt(indexNew--,'2');
str.setCharAt(indexNew--,'%');
}else {
// 没有遇到空格就直接复制
str.setCharAt(indexNew--,str.charAt(indexOld));
}
}
return str.toString();
}
}
注:合并两个数组(包括字符串)时,如果从前往后复制每个数字(或字符)需要重复移动数字(或字符)多次,那么我们可以考虑从后往前复制,这样就能减少移动的次数,从而提高效率
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
ArrayList<Integer> arrayList = new ArrayList<>();
while (listNode != null){
arrayList.add(listNode.val);
listNode = listNode.next;
}
for (int i = 0; i < arrayList.size()/2; i++) {
int temp = arrayList.get(i);
arrayList.set(i,arrayList.get(arrayList.size()-i-1));
arrayList.set(arrayList.size()-i-1,temp);
}
return arrayList;
}
对于链表似乎没有办法从后先前遍历,因此才有了开辟一个集合从前向后遍历并保存数据,再反转集合的方法,但是如果使用递归的话完全可以不用反转集合,如果不清楚可以思考回溯法是怎么实现的。
public class Solution {
private ArrayList<Integer> arrayList=new ArrayList<Integer>();
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
if(listNode!=null){
// 采用递归一直遍历到链表的尾部
printListFromTailToHead(listNode.next);
// 遍历的尾部后,添加元素
arrayList.add(listNode.val);
}
return arrayList;
}
}
这道题目首先要明白如何根据遍历得到的结果构建出二叉树:对一棵二叉树进行遍历,我们可以采取3中顺序进行遍历,分别是前序遍历、中序遍历和后序遍历,这三种方式是以访问父节点的顺序来进行命名的。假设父节点是N,左节点是L,右节点是R,那么对应的访问遍历顺序如下:
- 前序遍历 N->L->R
- 中序遍历 L->N->R
- 后序遍历 L->R->N
所以,对于以下这棵树,三种遍历方式的结果是
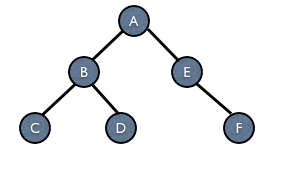
- 前序遍历 ABCDEF
- 中序遍历 CBDAEF
- 后序遍历 CDBFEA
已知二叉树的前序遍历和中序遍历,如何得到它的后序遍历
其实,只要知道其中任意两种遍历的顺序,我们就可以推断出剩下的一种遍历方式的顺序,这里我们只是以:知道前序遍历和中序遍历,推断后序遍历作为例子,其他组合方式原理是一样的。要完成这个任务,我们首先要利用以下几个特性:
- 特性A,对于前序遍历,第一个肯定是根节点;
- 特性B,对于后序遍历,最后一个肯定是根节点;
- 特性C,利用前序或后序遍历,确定根节点,在中序遍历中,根节点的两边就可以分出左子树和右子树;
- 特性D,对左子树和右子树分别做前面3点的分析和拆分,相当于做递归,我们就可以重建出完整的二叉树;
我们以一个例子做一下这个过程,假设:前序遍历的顺序是: CABGHEDF 中序遍历的顺序是: GHBACDEF
第一步,我们根据特性A,可以得知根节点是C,然后,根据特性C,我们知道左子树是:GHBA,右子树是:DEF。
C
/ \
GHBA DEF
第二步,取出左子树,左子树的前序遍历是:ABGH,中序遍历是:GHBA,根据特性A和C,得出左子树的父节点是A,并且A没有右子树。
C
/ \
A DEF
/
GBH
第三步,使用同样的方法,前序是BGH,中序是GHB,得出父节点是B,GH是左子树,没有右子树。
C
/ \
A DEF
/
B
/
GH
第四步,前序是GH, 中序是GH, 所以 G是父节点, H是右子树, 没有左子树.
C
/ \
A DEF
/
B
/
G
\
H
第四步,回到右子树,它的前序是EDF,中序是DEF,依然根据特性A和C,得出父节点是E,左右节点是D和F。
C
/ \
A E
/ / \
B D F
/
G
\
H
至此变得到了完整的二叉树,那么其后序遍历就是 : HGBADFEC
根据上面的描述在本题中可画图如下,那么就是递归不断的进行分割左右子树的过程。
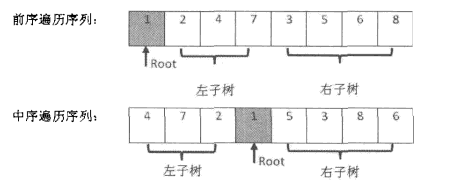
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
return root;
}
//前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
// 递归的终止条件,当前序或中序数组有一方结束,递归便终止
if(startPre>endPre||startIn>endIn){
return null;
}
TreeNode root=new TreeNode(pre[startPre]);
for(int i=startIn;i<=endIn;i++) {
if (in[i] == pre[startPre]) {
// 左子树递归,联系两个数组确定起始和终止位置
root.left = reConstructBinaryTree(pre, startPre + 1, startPre + i - startIn, in, startIn, i - 1);
// 右子树递归,联系两个数组确定起始和终止位置
root.right = reConstructBinaryTree(pre, startPre + i - startIn + 1, endPre, in, i + 1, endIn);
break;
}
}
return root;
}
}
本题与LeetCode 232 题目基本一致,这里给出的代码是左程云的程序员面试指南一书中的答案,但基本思路是一致的都是一个先用一个栈存储,出队时再用另一栈进行转换。但有两个基本的原则:
(1)当弹出栈不为空的时候存储栈是不能向其导入数据的
(2)每次导入数据必须要把存储栈的数据全部导入。
public class Solution {
Stack<Integer> stack1 = new Stack<Integer>();
Stack<Integer> stack2 = new Stack<Integer>();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if(stack1.empty()&&stack2.empty()){
throw new RuntimeException("Queue is empty!");
}
if(stack2.empty()){
while(!stack1.empty()){
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
}
这个小节虽是查找和排序但主要还是查找。查找有:顺序查找、二分法、哈希表、二叉树排序查找。在一个有序或者部分有序的数组中查找一个数字或者是统计数字出现的频率都可以采用二分法查找的。
(1)旋转数组的最小数字。
剑指offer写的太垃圾了,唯一有用的就这两个图了,代码主要参考的是程序员代码面试指南第9章部分
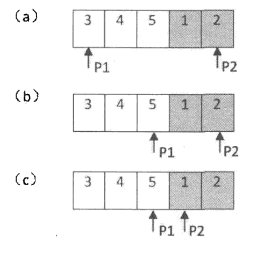
特例:对数字{0, 1, 1, 1, 1}的两个旋转{1, 0, 1, 1, 1}、{1, 1, 1, 0, 1}如下图所示:

public int gerMin(int[] nums) {
int left = 0;
int right = nums.length-1;
int mid = 0;
while (left < right){
if (left == right-1){
break;
}
if (nums[left] < nums[right]){//因为是递增的,如果左侧部分数小则说明left到right没有旋转,断点就是nums[left]
return nums[left];
}
mid = (left+right)/2;//定位中间位置
if (nums[left] > nums[mid]){ //如果左侧部分大,说明断点在左侧
right = mid;
continue;
}
if (nums[mid] > nums[right]){//说明断点在右侧
left = mid;
continue;
}
//当上面没有命中时,说明nums[left]==nums[mid]==nums[right],此时直接顺序遍历方法有点笨
// 可以继续创造二分条件
while (left < right){
if (nums[left] == nums[mid]){//先在左侧遍历寻找断点
left++;
}else if (nums[left] < nums[right]){//当左侧不满足条件时,此时left就是左侧断点
return nums[left];
}else {//在右侧寻找断点
right = mid;
break;
}
}
}
return Math.min(nums[left],nums[right]);
}
这里分别对应着牛客网题目:斐波那契数列、跳台阶、变态台阶,其本质都是动态规划,在博客中https://www.cnblogs.com/youngao/p/11453374.html已经有记录过了,在这里记录下变态跳台阶,对于4阶楼梯其递归图如下:
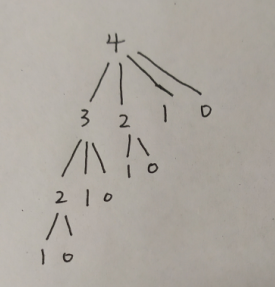
那么递推公式为:
f(n) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2) + f(n-1) = f(n-1) + f(n-1)
f(n-1) = f(0) + f(1)+f(2)+f(3) + ... + f((n-1)-1) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2)
那么可以推出:
f(n) = 2*f(n-1)。其动态规划写法为:
public int JumpFloorII(int target) {
if (target == 1){
return 1;
}
int[] arr = new int[target+1];
arr[1] = 1;
for (int i = 2; i <= target ; i++) {
arr[i] = 2*arr[i-1];
}
return arr[target];
}
对于举行覆盖这个题目,和上面类似,但问题的关键是如何理解题目,此时的f(2)、f(1)不再是单纯的数字了而是代表一种状态或者一种情况。
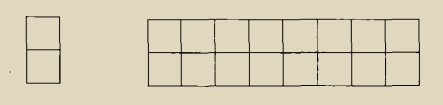
f(1)代表1*2、f(2)代表着2*2的情况,有2种情况。对于f(3)可以先竖着然后是f(2)也可以先横着然后是f(1),因此所有的情况为f(1)+f(2),对于后面的情况也是如此,对于代码部分其实是和前面的斐波那契数列是一样的因此不再记录代码。
本题一开始自己写的代码如下,出现的问题也比较多。
public int NumberOf1(int n) {
int count = 0;
while (n != 0){
if (n%2 == 1){
count++;
}
n = n/2;
}
return count;
}
首先n=n/2这一步完全可以用为运算代替的,其次,n%2这一步也可以考虑位运算的,还有整个算法只适合n大于0的情况,当n小于n时由于补码的原因是不能直接这样算法的。
public int NumberOf1(int n) {
int count = 0;
// 当为负数时使用补码符号位为1,移位的时候符号位也要移位的最后再补1,那么最后的结果就是0xffffffff,陷入了死循环中,我在提交代码时使用了n=-n竟然没通过
if (n < 0){
n = n &0x7fffffff;
count++;
}
while (n != 0){
// 这里不再取余,直接与1与获取最低位是否为1
count = count + (n&1);
n = n>>1;
}
return count;
}
对于上面的代码其效率还可再提高:把一个整数减去1,再和原整数做与运算,会把该整数最右边一个1变成0.那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。
public int NumberOf1(int n) {
int count = 0;
while (n != 0){
n = (n-1) & n;
count++;
}
return count;
}
3 高质量的代码
public double Power(double base, int exponent) {
double res = 1.0;
if (exponent == 0){
return 1;
}
if (exponent > 0){
for (int i = 1; i <= exponent; i++) {
res = res * base;
}
}else {
for (int i = 1; i <= -exponent; i++) {
res = res * base;
}
return 1.0/res;
}
return res;
}
上面的代码虽然可以解决问题,但是效率不高,完全可以提升的。对于求一个数的n次方可以写成如下的公式,那么其时间复杂度为O(logn)
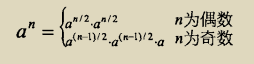
剑指offer中的代码太垃圾了,在测试时有bug的,因此采用LeetCode上的代码,这道题目在LeetCode50-Pow(x,n)
public double myPow(double x, int n) {
long N = n; //定义为long就是因为int中负数的范围大
if (N < 0){ //当为负数数时应该把最后的除法变成乘法,要不然会出现Infinity
x = 1/x;
N = -N;
}
return fastPow(x,N);
}
private double fastPow(double x, long n) {
if (n == 0){
return 1.0;
}
//折半计算
double half = fastPow(x,n/2);
//返回时要考虑奇偶性
return n%2==0 ? half*half : half*half*x;
}
与这道题目类似的有LeetCode231 2的幂,可以借鉴上面的思路使其时间复杂度为O(logN),但对于这道题目还有更好的方法。
题目中有提示:相对位置不变--->保持稳定性;奇数位于前面,偶数位于后面 --->存在判断,挪动元素位置。那么根据这两点便可以借用插入排序的思想,两两比较,一下的代码其是就是插入排序的代码,只不过是把判断条件给修改了一下。
public class Solution {
public void reOrderArray(int [] array) {
//判断需不需要排序
if (array == null || array.length < 2) {
return;
}
//外层控制起始位置,内层从起始位置向前遍历
for (int i = 0; i < array.length-1; i++) {
// 为了效率的提高,对2取余的操作变成了与0x01相与,为0便是偶数为1便是奇数
for (int j = i ; j >= 0 && ((array[j] & 0x01)==0) && ((array[j + 1] & 0x01) ==1); j--) {
swap(array, j, j + 1);
}
}
}
private void swap(int[] arr,int m,int n){
int temp = arr[m];
arr[m] = arr[n];
arr[n] = temp;
}
}
鲁棒性:程序能够判断输入是否合乎规范要求,并对不合要求的输入予以处理。
这道题目中为了说清楚举例如下:1、2、3、4、5那么倒数第2个节点便是4。这道题目和LeetCode 19(算法面试3--链表 4)删除链表倒数第N个节点是类似的使用双指针遍历即可,当不同之处这里要处理k大于链表节点长度的情况,因此还是稍有不同,注意其判断条件。
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
ListNode p1 = head;
ListNode p2 = head;
// 当链表为空或者k为0时返回空
if (head == null || k == 0){
return null;
}
while (--k != 0 ){
p2 = p2.next;
if (p2 == null){
return null;
}
}
// 终止条件的修改是关键
while (p2.next != null){
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}
这道题目和LeetCode 206(算法面试3--链表 1)是一样的。
这道题目和LeetCode 21是一样的。
例子如下,查找过程可以分为两步,第一步找到相同的根节点,第二部判断根节点的子节点是否相同。在第一步找到相同的根节点可以认为是树的遍历操作可以用递归来实现,对于第二步的判断也可以用递归来实现。
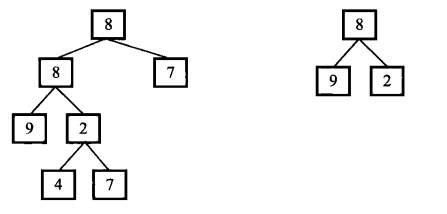
public class Solution {
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
boolean res = false;
//当Tree1和Tree2都不为零的时候,才进行比较。否则直接返回false
if (root1 != null && root2 != null){
//如果找到了对应Tree2的根节点的点
if (root1.val == root2.val){
//以这个根节点为为起点判断是否包含Tree2
res = doesTree1HaveTree2(root1,root2);
}
//如果找不到,那么就再去root的左儿子当作起点,去判断时候包含Tree2
if (!res){
res = HasSubtree(root1.left,root2);
}
//如果找不到,那么就再去root的右儿子当作起点,去判断时候包含Tree2
if (!res){
res = HasSubtree(root1.right,root2);
}
}
return res;
}
// 判断以根节点为起点的子树是否包含Tree2
private boolean doesTree1HaveTree2(TreeNode node1, TreeNode node2) {
//如果Tree2已经遍历完了都能对应的上,返回true
if (node2 == null){
return true;
}
//如果Tree2还没有遍历完,Tree1却遍历完了。返回false
if (node1 == null){
return false;
}
//如果其中有一个点没有对应上,返回false
if (node1.val != node2.val){
return false;
}
//如果根节点对应的上,那么就分别去子节点里面匹配
return doesTree1HaveTree2(node1.left,node2.left) && doesTree1HaveTree2(node1.right,node2.right);
}
}
上面的代码还是可以进行优化的,只给出可以优化部分的代码
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
boolean res = false;
if (root1 != null && root2 != null){
if (root1.val == root2.val){
res = doseHas(root1.left,root2.left) && doseHas(root1.right,root2.right);
}
if (!res){
res = (HasSubtree(root1.left,root2) || HasSubtree(root1.right,root2));
}
}
return res;
}
第4章 解决面试题的思路
总结:在写代码前要想清楚思路和设计,并分析好边界条件。对于问题的分析一般有:画图、举例、分解三种方法。
本题与LeetCode 226题目类似,在博客算法面试5--1 二叉树中有代码讲解。
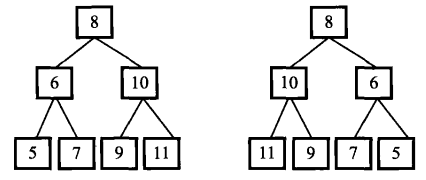
相关题目:在LeetCode101-对称二叉树来判断二叉树是否是对称的,也要看一下
剑指offer中的解析太繁琐没看懂,直接看的程序代码面试指南中的思路。
本题不涉及到任何数据结构但是涉及到了诸多的边界条件和循环,因此比较复杂,打印的过程,如果去考虑每一圈的范围的变化就造成变量太多难以控制。在矩阵中可以通过左上、右下两点便可以限制一个矩阵的大小。
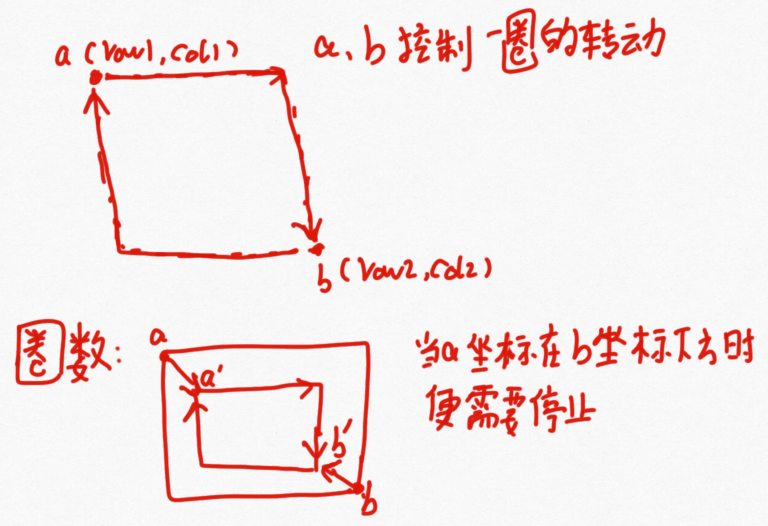
public ArrayList<Integer> printMatrix(int [][] matrix) {
int row = matrix.length;
int col = matrix[0].length;
//输入的二维数组非法
if (row == 0 || col == 0){
return null;
}
ArrayList<Integer> res = new ArrayList<>();
//定义四个变量,分别表示左上和右下的打印范围
int row1=0,col1=0,row2=row-1,col2=col-1;
while (row1 <= row2 && col1 <= col2){
if (row1 == row2){ //当矩阵只有一行时
for (int i = col1; i <= col2; i++) {
res.add(matrix[row1][i]);
}
}else if (col1 == col2){ // 当 +矩阵只有一列时
for (int i = row1; i <= row2; i++) {
res.add(matrix[i][col1]);
}
}else { //一般情况
int curC = col1;
int curR = row1;
while (curC != col2) {
res.add(matrix[row1][curC]);
curC++;
}
while (curR != row2) {
res.add(matrix[curR][col2]);
curR++;
}
while (curC != col1) {
res.add(matrix[row2][curC]);
curC--;
}
while (curR != row1) {
res.add(matrix[curR][col1]);
curR--;
}
}
//左上角的点向下移动
row1++;col1++;
//右下角的点向上移动
row2--;col2--;
}
return res;
}
本题的虽然有入栈,出栈,获取最小值,但关键还是如何入栈,因为时间复杂度要求O(1),出栈的时候还要按照压入的顺序出栈因此需要用一个辅助栈来保存每添加一个新的数字后得到的最小值,这样出栈操作正常进行,当需要获取最小值时直接从最小栈获取即可。
// 数据栈用来保存每次存入的数据
private Stack<Integer> data = new Stack<>();
// 最小栈,用来保存每次存入新数据后的当前最小值
private Stack<Integer> min = new Stack<>();
public void push(int node) {
// 存放数据
data.add(node);
if (min.size() == 0 || node < min.peek()){
// 当最小栈为空或者栈顶元素大时,把新的最小值存放入最小栈中
min.add(node);
}else {
min.add(min.peek());
}
}
画图分析压入弹出过程,可以总结规律如下:如果下一个弹出的数字刚好是栈顶数字,那么直接弹出。如果下一个弹出的数字不在栈项,我们把压栈序列中还没有入栈的数字压入辅助栈,直到把下一个需要弹出的数字压入找顶为止。如果所有的数字都压入栈了仍然没有找到下一个弹出的数字,那么该序列不可能是一个弹出序列。根据以上规律得到代码如下:
public class Solution {
public boolean IsPopOrder(int [] pushA,int [] popA) {
Stack<Integer> stack = new Stack<>();
// 弹出栈的指针
int j = 0;
for (int i = 0; i < pushA.length; i++) {
// 存入压入的数据
stack.add(pushA[i]);
while (j < popA.length){
// 先保存数据的栈不为空,再判断是否与输出栈的序列相同
if (!stack.isEmpty() && stack.peek() == popA[j]){
stack.pop();
j++;
}else {
break;
}
}
}
return stack.isEmpty();
}
}
本题与LeetCode 102一样的均是广度优先遍历,但102是稍微提高了一下还要有null本题先对来说简单,可以参考算法与数据结构学习2-5所示。
public class Solution {
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
if (root == null){
// 因为返回形式的限制,这里直接返回null不通过
return res;
}
queue.add(root);
while (!queue.isEmpty()){
TreeNode temp = queue.poll();
if (temp.left != null){
queue.add(temp.left);
}
if (temp.right != null){
queue.add(temp.right);
}
res.add(temp.val);
}
return res;
}
}
对于一个树而言,其前序中序后序为:前序顺序是ABC(根节点排最先,然后同级先左后右);中序顺序是BAC(先左后根最后右);后序顺序是BCA(先左后右最后根)
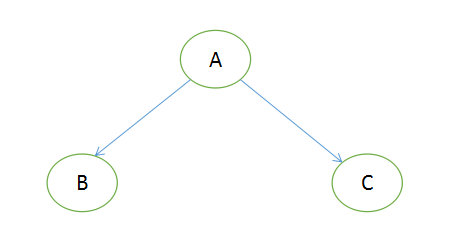
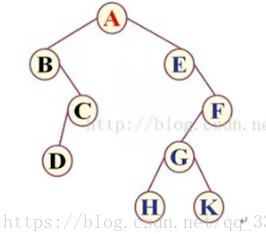
如上图二叉树遍历结果:
前序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
本题把后序遍历和二分搜索树的性质结合在一起,对于一个二分搜索树,其后序遍历为:5、7、6、9、11、10、 8
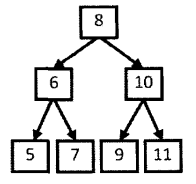
在上例中,后序遍历结果的最后一个数字8就是根结点的值。在这个数组中,前3个数字5、7和6都比8小,是值为8的结点的左子树结点;后3个数字9、11和10都比8大,是值为8的结点的右子树结点。后面可以用递归的形式确定,对于序列5、7、6,最后一个数字6是左子树的根结点,5比6小是6的左子树,7是右子树,对于另外一部分即同样处理即可。
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence.length == 0){
return false;
}
// 对长度为1的特殊处理一下
if (sequence.length == 1){
return true;
}
return judge(sequence,0,sequence.length-1);
}
// 判断是否是二分搜索树的后序序列
private boolean judge(int[] sequence, int start, int root) {
// 递归的终止条件
if (start >= root){
return true;
}
int i = root;
// 从后向前找,遍历右子树
while (i > start && sequence[i-1]>sequence[root]){
i--;
}
// 从前先后找,遍历左子树
for (int j = start; j < i-1; j++) {
// 如果j没到i-1处就有比根节点大的数字,说明不符合二分搜索树的性质,返回false
if (sequence[j]>sequence[root]){
return false;
}
}
// 递归遍历左子树,右子树,只有两边都为都为true时才是真正的二分搜索树
return judge(sequence,start,i-1) && judge(sequence,i,root-1);
}
}
注:处理一颗二叉树的遍历,一般是先找到二叉树的根节点,然后再基于根节点把整棵树的遍历序列分为左子树和右子树序列,然后再递归处理左子树和右子树序列。
本题与LeetCode 113 题目基本一致的,可以参考LeetCode题解。
对于一个复杂链表其构成可能如下图所示:
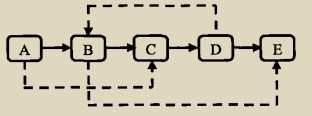
一开始想的是直接复制不就可以了,遍历过去后直接每个节点都指向一次,但这样做会造成一个问题就是出现两个相同的节点。
出现重复节点的代码:
private void copy(RandomListNode pHead){
RandomListNode walkNode = pHead;
RandomListNode res = pHead;
if (walkNode.next != null){
RandomListNode cloneNode = new RandomListNode(walkNode.next.label);
RandomListNode clone2Node = new RandomListNode(walkNode.random.label);
res.next = walkNode.next;
res.random = clone2Node;
}
}
那么一个思路就是可以把这些拷贝的节点存储在集合中,在集合中设置节点的random指针。
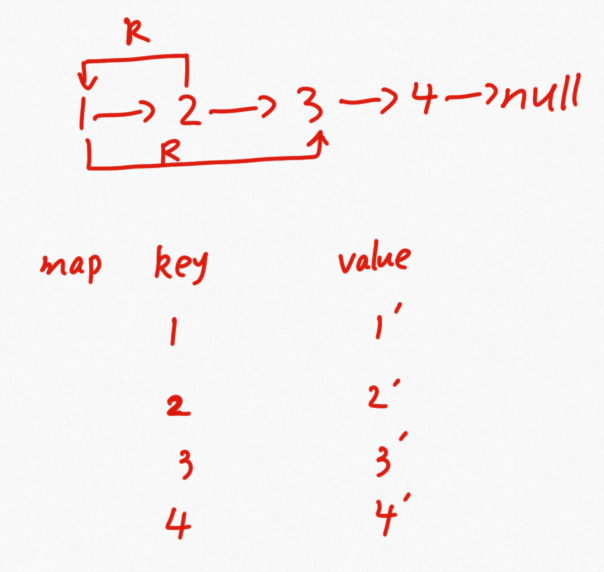
public static Node copyListWithRand1(Node head) {
HashMap<Node, Node> map = new HashMap<Node, Node>();
Node cur = head;
//复制节点并存入map集合中
while (cur != null) {
map.put(cur, new Node(cur.value));
cur = cur.next;
}
cur = head;
//在map集合中设置连接
while (cur != null) {
map.get(cur).next = map.get(cur.next);
map.get(cur).rand = map.get(cur.rand);
cur = cur.next;
}
return map.get(head);
}
方法二:不用额外空间。
第一步:根据原始链表的每个节点N创建对应的N',并把N'连接在N后面。
第二步:为复制结点的random指针赋值。如果原结点的random指针指向的是结点B,那么将复制结点的random指针指向结点B的复制结点B'
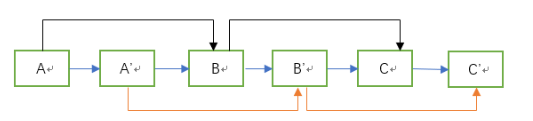
第三步:将链表的原始结点与复制结点分割至两个链表,使原始结点构成一个链表,复制结点构成一个链表。
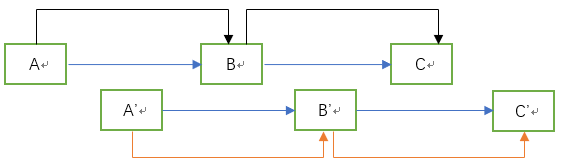
剑指offer中的代码太繁琐了
public Node copyRandomList(Node head) {
if (head == null){
return null;
}
Node cur = head;
Node next = null;
//把链表复制并进行连接
while (cur != null){
next = cur.next;
cur.next = new Node(cur.val);
cur.next.next = next;
cur = next;
}
cur = head; //从头开始遍历
Node curCopy = null;//指向拷贝的节点
while (cur != null){
next = cur.next.next;//因为每两个节点中间有一个拷贝节点所以每次走两步
curCopy = cur.next;
curCopy.random = cur.random != null ? cur.random.next : null;
}
Node res = head.next;//结果节点
cur = head;
while (cur != null){ //拆分链表
next = cur.next.next;
curCopy = cur.next;
cur.next = next;
curCopy.next = next != null ? next.next : null;
cur = next;
}
return res;
}
对于转换如下图所示:
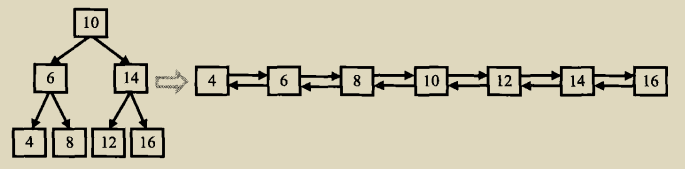
由二分搜索树的性质可知,排好序可以用中序遍历,对于上面的二分搜索树可以看成三部分:根节点、左子树、右子树。
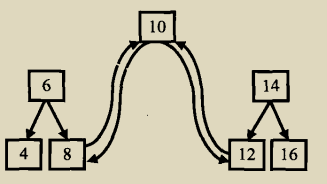
把左右子树都转换成排序的双向链表后再和根节点相连接,这样就完成了转换。
public class Solution {
//当前节点的前一个节点
private TreeNode pre = null;
//返回的头节点
private TreeNode head = null;
public TreeNode Convert(TreeNode pRootOfTree) {
solve(pRootOfTree);
return head;
}private void solve(TreeNode node){
if(node == null) return;
//中序递归处理
solve(node.left);
if(pre == null){
pre = node;
head = node;
}else{
//设定双向连接
pre.right = node;
node.left = pre;
pre = node;
}
solve(node.right);
}
}
剑指offer中采用的交换方法,不过感觉不太好还是采用回溯法在算法模板中有记录也可以参考LeetCode 46、47全排列问题。
这道题目是有重复字母的情况,直接考虑比较麻烦,先来看没有重复数字的情况。
以1、2、3为例:1 2 3。1 3 2。2 1 3。2 3 1。3 2 1。3 1 2。共有6种情况,但是其实可以这样来看:
分别对以1开头,以2开头,以3开头的做全排列,在剩下的两个数中又是先固定出一个数然后继续做全排列,这样依次递归下去。那么问题的关键在于如何在于如何固定元素,上例中可以看出:认为是1与2交换了位置,1与3交换了位置,实现了2、3分别在首部,因此如何排在首部是借用交换实现的。
代码实现:
//为了做铺垫这里采用字符串abc,与数字是一样的原理
public ArrayList<String> Permutation(String str) {
//用来保存结果
ArrayList<String> res = new ArrayList<>();
if (str != null && str.length() > 0)
helper(str.toCharArray(),0,res);
return res;
}
private void helper(char[] chars, int index,ArrayList<String> res) {
if (index == chars.length-1){
res.add(String.valueOf(chars));
return;
}
for (int i = index; i < chars.length; i++) {
//index指向固定位置,依次进行交换操作
swap(chars,index,i);
//交换后递归
helper(chars,index+1,res);
//复原
swap(chars,index,i);
}
}
有重复字母的情况:
在上面的无重复情况是进行了交换,那么因为有重复时相同两个交换是一样的也就是说当有重复字母时是不需要进行交换的。因为字母是随机分配的,有些重复的不太好记录,那么可以用借用hashSet来实现过滤重复元素。
代码实现:
public class Solution {
public ArrayList<String> Permutation(String str) {
ArrayList<String> list = new ArrayList<>();
if (str != null && str.length() > 0){
helper(str.toCharArray(),0,list);
//题目中要求需要按照字典顺序输出
Collections.sort(list);
}
return list;
}
private void helper(char[] chars, int index, ArrayList<String> list) {
if (index == chars.length - 1){
list.add(String.valueOf(chars));
}else {
//将已经遍历过的元素存入hashSet集合中,当集合中没有存该元素时才发生交换
Set<Character> charSet = new HashSet<>();
for (int i = index; i < chars.length; i++) {
if (index == i || !charSet.contains(chars[i])){
charSet.add(chars[i]);
swap(chars,index,i);
helper(chars,index+1,list);
swap(chars,i,index);
}
}
}
}
// 交换操作
private void swap(char[] cs,int i,int j){
char temp = cs[i];
cs[i] = cs[j];
cs[j] = temp;
}
}
第5章 优化时间和空间效率
这里的想法是直接采用了HashMap保存频率。
本题与LeetCode 215、703类似需要借用一个堆来满足要求,本质上就是堆排序,其时间复杂度为O(nlogk),在这里需要用到的不是最小堆而是最大堆,那么最小堆和最大堆之间的转换只需要重写比较方法即可。题目中给出的示例输出数据是有序的,其实输出数据有序无序是不要求的。
public class Solution {
public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
// 最大堆需要重写比较方法
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
ArrayList<Integer> res = new ArrayList<>();
// 提交的时候需要考虑的边界条件
if (input.length < k || input.length == 0 || k == 0){
return res;
}
for (int i = 0; i < input.length; i++) {
if (maxHeap.size() < k){
maxHeap.add(input[i]);
}else{
if (input[i] < maxHeap.peek()){
maxHeap.remove();
maxHeap.add(input[i]);
}
}
}
int n = maxHeap.size();
for (int i = 0; i < n; i++) {
res.add(maxHeap.remove());
}
return res;
}
}
本题一开始想着利用双指针遍历,但是当遇到负数时移动左指针还是右指针无法确定,因此这个思路是错误的。求连续的数组n的最大和,但不要把连续数组的长度和最大和混为一谈,在遍历的时候当遇到负数时是否添加是根据数组的情况决定的,但是最大和却不一定会更新,只能说在寻找子数组时尽可能保证和最大。采用动态规划,其递归函数如下:
F(i):以array[i]为末尾元素的子数组的和的最大值,子数组的元素的相对位置不变
F(i)=max(F(i-1)+array[i] , array[i])
res:所有子数组的和的最大值
public class Solution {
public int FindGreatestSumOfSubArray(int[] array) {
// 初始状态
int res = array[0];
int max = array[0];
// 动态规划
for (int i = 1; i < array.length; i++) {
// 比较判断是否添加下一个数字
max = Math.max(max+array[i],array[i]);
// 并不是更新完一次序列后最大和就要修改,还有比较的
res = Math.max(max,res);
}
return res;
}
}
注:其实在剑指offer中给出了一个要求使用时间复杂度为O(n),可以说也算是给出了一个提示。
本题与LeetCode 233一样,一开始想的是如下代码,其时间复杂度为O(nlogn)但是这样无法AC因为时间复杂度不符合题目要求
public class Solution {
public int NumberOf1Between1AndN_Solution(int n) {
int res = 0;
for (int i = 1; i <=n ; i++) {
while (i != 0){
if (i % 10 == 1){
res++;
}
n = n/10;
}
}
return res;
}
}
原本打算采用动态规划的方法优化,但是仔细看了一下因为所有res++,我用动态规划还有计算每次从1到n中1的个数,基本相当于没有任何优化,还浪费了空间。本题要解决关键在于数学规律的应用,在这里可以参考博客https://blog.youkuaiyun.com/yi_afly/article/details/52012593
数学规律:
534 = (个位1出现次数)+(十位1出现次数)+(百位1出现次数)=(53*1+1)+(5*10+10)+(0*100+100)= 214
530 = (53*1)+(5*10+10)+(0*100+100) = 213
504 = (50*1+1)+(5*10)+(0*100+100) = 201
514 = (51*1+1)+(5*10+4+1)+(0*100+100) = 207
10 = (1*1)+(0*10+0+1) = 2
代码实现:参考牛客网讨论区解答
/*
设N = abcde ,其中abcde分别为十进制中各位上的数字。
如果要计算百位上1出现的次数,它要受到3方面的影响:百位上的数字,百位以下(低位)的数字,百位以上(高位)的数字。
① 如果百位上数字为0,百位上可能出现1的次数由更高位决定。比如:12013,则可以知道百位出现1的情况可能是:100~199,1100~1199,2100~2199,,...,11100~11199,一共1200个。可以看出是由更高位数字(12)决定,并且等于更高位数字(12)乘以 当前位数(100)。
② 如果百位上数字为1,百位上可能出现1的次数不仅受更高位影响还受低位影响。比如:12113,则可以知道百位受高位影响出现的情况是:100~199,1100~1199,2100~2199,,....,11100~11199,一共1200个。和上面情况一样,并且等于更高位数字(12)乘以 当前位数(100)。但同时它还受低位影响,百位出现1的情况是:12100~12113,一共114个,等于低位数字(113)+1。
③ 如果百位上数字大于1(2~9),则百位上出现1的情况仅由更高位决定,比如12213,则百位出现1的情况是:100~199,1100~1199,2100~2199,...,11100~11199,12100~12199,一共有1300个,并且等于更高位数字+1(12+1)乘以当前位数(100)。
*/
public int NumberOf1Between1AndN_Solution(int n) {
if (n<1) return 0;
int count = 0;//1的个数
int base = 1;//基准进制
int current =0,after = 0,before =0;
while((n/base)!=0){
current = (n/base)%10;//当前位数字
before = n/(base*10);//高位数字
after = n - (n/base)*base;//低位数字
//若当前位为0,出现1的次数由高位决定,等于高位数字*当前基准进制
if(current == 0)
count += before*base;
//若当前位为1,出现1的次数由高位和低位决定,高位*当前基准进制+低位+1,加1是因为还以一个10
else if(current == 1)
count += before*base+after+1;
//若当前位大于1,出现1的次数由高位决定,(高位+1)*当前基准进制
else
count += (before+1)*base;
//基准进制变更
base *= 10;
}
return count;
}
这道题目其实是希望我们能够找到一个排序规则,数组根据这个规则排序之后能排成一个最小的数字。要确定排序规则,就要比较两个数字,也就是给出两个数字m和n,我们需要确定一个规则判断m和n哪个应该排在前面,而不是仅仅比较这两个数字的值哪个更大。
确立规则:根据题目的要求,两个数字m和n能拼成数字mn和nm。如果mn<nm,那么我们应该打印出mn,即m应该排在n的前面,我们此时定义m小于n;反之,如果nm<mn,我们定义n小于m。如果mn=nm,我们定义m等于n。(注:符号的<,>, =是常规意义的数值大小,而文字的“大于”,“小于”,“等于”表示我们新定义的大小关系)。
因存在大数问题,故我们把数字转化为字符串,另外把数字m和数字n拼接起来得到mn和nm,它们的位数肯定是相同的,因此比较它们的大小只需要按照字符串大小的比较规则就可以了。
public class Solution {
public String PrintMinNumber(int [] numbers) {
if (numbers == null || numbers.length == 0){
return "";
}
int len = numbers.length;
String[] str = new String[len];
// 因为后面要进行数字的组合,因此直接在使用整数不方便了
for (int i = 0; i < len; i++) {
str[i] = String.valueOf(numbers[i]);
}
// 这里自定义排序规则
Arrays.sort(str, new Comparator<String>() {
@Override
public int compare(String o1, String o2) {
String str1 = o1 + o2;
String str2 = o2 + o1;
return str1.compareTo(str2);
}
});
// 把字符串数组转为字符串
StringBuilder sb = new StringBuilder();
for (int i = 0; i < len; i++) {
sb.append(str[i]);
}
return sb.toString();
}
}
直接去考虑质因子会导致时间复杂度较高,就像前面的判断从1到n有多少个1一样,因此有两种方案,要么从数学的角度考虑,要么优化算法。有数学性质可知,下一个丑数应该是前面的丑数分别与2 3 5 相乘,取其大于当前丑数最小的一个。这样下一个数字由前一个数字得到的思路,可以考虑采用动态规划的方法
public class Solution {
public int GetUglyNumber_Solution(int index) {
if (index < 1){
return 0;
}
// 1是第一个丑数
if (index == 1){
return 1;
}
int[] arr = new int[index+1];
arr[1] = 1;
// 分别记录与2 3 5相乘的索引,每个索引的代表的就是当前的数字是由哪个因子的第几个数得来的
// 每次相乘用最大索引下的值这样对于一些较小的数字就可以避免无谓的计算了
int t2 = 1,t3 = 1,t5 = 1;
// 动态规划
for (int i = 2; i <= index; i++) {
// 取其最小的一个
arr[i] = Math.min(arr[t2]*2,Math.min(arr[t3]*3,arr[t5]*5));
if (arr[i] == arr[t2]*2){
t2++;
}
if (arr[i] == arr[t3]*2){
t3++;
}
if (arr[i] == arr[t3]*5){
t5++;
}
}
return arr[index];
}
}
可以利用数组进行保存,对于这种形式的保存因为涉及到key和value的形式一般也称为hash表。
public int FirstNotRepeatingChar(String str) {
if (str == null || str.length() == 0){
return -1;
}
//利用一个长度为58的数组来存储数据
// A-Z的ASCII码为65-90,a-z对应的97-122 因此122-65=57
int[] words = new int[58];
for (int i = 0; i < str.length(); i++) {
words[str.charAt(i)-'A'] ++;
}
for (int i = 0; i < str.length(); i++) {
if (words[str.charAt(i)-'A'] == 1){
return i;
}
}
return -1;
}
注:当需要判读多个字符出现的次数时,可以利用数组构建一个hash表,但当判断数字的频率时由于数字的大小不确定因此一般用hashMap。
采用归并排序的思路解决
//统计逆序对的个数
private int count=0;
//辅助数组
private int[] aux;
public int InversePairs(int [] array) {
if(array == null || array.length < 2) return 0;
aux = new int[array.length];
mergeCount(array,0,array.length-1);
return count;
}
//归并排序的实现
private void mergeCount(int[] arr,int left,int r){
if(left >= r) return;
int mid = left+(r-left)/2;
//递归拆分
mergeCount(arr,left,mid);
mergeCount(arr,mid+1,r);
//进行归并
merge(arr,left,mid,r);
}
//归并实现
private void merge(int[] arr,int left,int mid,int r){
int i = left,j = mid+1;
//先把两部分数据都复制到一个数组中
for(int k = left;k<=r;k++)
aux[k] = arr[k];
//进行合并计数
for(int k=left;k<=r;k++){
if(i > mid)
arr[k] = aux[j++];
else if(j > r)
arr[k] = aux[i++];
else if(aux[i] <= aux[j]){
//若前面的数小于后面直接存进去,并移动前面数的指针
arr[k] = aux[i++];
}else if(aux[i] > aux[j]){
//前面的数大于后面则有逆序对产生
arr[k] = aux[j++];
//从a[i]开始到a[mid]必定都是大于这个a[j]的,因为此时分治的两边已经是各自有序了
count = (count+mid-i+1)%1000000007;
}
}
}
本题与LeetCode 160是相同的,因此不再详细解释。但这里比LeetCode上要多考虑一些情况,比如有可能存在两个链表根本就没有交点的情况,LeetCode默认是有交点的。
代码实现:
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
if (pHead1 == null || pHead2 == null){
return null;
}
ListNode node1 = pHead1;
ListNode node2 = pHead2;
while (node1 != null || node2 != null){
if (node1 == null){
node1 = pHead2;
}
if (node2 == null){
node2 = pHead1;
}
//要先判断是否相等然后在移动,否则可能会少判断一位
if (node1 == node2){
return node1;
}
node1 = node1.next;
node2 = node2.next;
}
return null;
}
第6章 面试中的各项能力
题目中有些并没有解释清楚,这里的排序数组是按照升序的设定的,题目中已经给出了有序,那么首先就要考虑是否能否使用二分法查找了,如果不能直接使用那么是否可以改造后使用。此处对二分法进行了改造,便可以查找到最后一个和第一个数字出现的索引。
这里采用算法小抄一书中的代码,剑指offer中在理解上没有这个简单,用二分查找分别找到左右边界即可
public int GetNumberOfK(int [] array , int k) {
if(array == null || array.length == 0) return 0;
return right_bound(array,k)-left_bound(array,k)+1;
}
//求出左边界的位置
public int left_bound(int[] nums, int target){
if(nums.length == 0) return -1;
int left = 0;
int right = nums.length;
while(left < right){
int mid = left+(right-left)/2;
if(nums[mid] == target){
right = mid;
}else if(nums[mid] < target){
left = mid+1;
}else if(nums[mid] > target){
right = mid;
}
}
return left;
}
//求出右边界的位置
public int right_bound(int[] nums, int target){
if(nums.length == 0) return -1;
int left = 0;
int right = nums.length;
while(left < right){
int mid = left+(right-left)/2;
if(nums[mid] == target){
left = mid+1;
}else if(nums[mid] < target){
left = mid+1;
}else if(nums[mid] > target){
right = mid;
}
}
return left-1;
}
剑指offer一书中的代码
public class Solution {
public int GetNumberOfK(int [] array , int k) {
int len = array.length;
if (len == 0){
return 0;
}
int firstK = getFirstK(array,k,0,len-1);
int lastK = getLastK(array,k,0,len-1);
if (firstK != -1 && lastK != -1){
return lastK-firstK+1;
}
return 0;
}
// 递归求第一k的索引
private int getFirstK(int[] array, int k, int start, int end) {
if (start > end){
return -1;
}
int mid = start+(end- start)/2;
if (array[mid] > k){
return getFirstK(array,k,start,mid-1);
}else if (array[mid] < k){
return getFirstK(array,k,start+1,end);
}else if (mid-1 >= 0 && array[mid-1] == k){
// 当mid所处的不是第一个k时,需要在前段进行遍历
return getFirstK(array,k,start,mid-1);
}else {
// 当mid为第一个k时,直接返回
return mid;
}
}
// 循环求最后一个k的索引
private int getLastK(int[] array, int k, int start, int end) {
while (start <= end){
int mid = start+(end- start)/2;
if (array[mid] > k){
end = mid-1;
}else if (array[mid] < k){
start = mid+1;
}else if (mid+1 < array.length && array[mid+1] == k){
// 当mid所处的不是最后一个k时,需要在后段进行遍历
start = mid+1;
}else {
// 当mid为最后一个k时,直接返回
return mid;
}
}
return -1;
}
}
本题与LeetCode 104是一样的。
本题与LeetCode 110是一样的。
首先我们考虑这个问题的一个简单版本:一个数组里除了一个数字之外,其他的数字都出现了两次。题目为什么要强调有一个数字出现一次,其他的出现两次?我们想到了异或运算的性质:任何一个数字异或它自己都等于0 。如果能够把原数组分为两个子数组。在每个子数组中,包含一个只出现一次的数字,而其它数字都出现两次。如果能够这样拆分原数组,按照前面的办法就是分别求出这两个只出现一次的数字了。
对于有两个数字的:我们还是从头到尾依次异或数组中的每一个数字,那么最终得到的结果就是两个只出现一次的数字的异或结果。因为其它数字都出现了两次,在异或中全部抵消掉了。由于这两个数字肯定不一样,那么这个异或结果肯定不为0 ,也就是说在这个结果数字的二进制表示中至少就有一位为1 。我们在结果数字中找到第一个为1 的位的位置,记为第N 位。现在我们以第N 位是不是1 为标准把原数组中的数字分成两个子数组,第一个子数组中每个数字的第N 位都为1 ,而第二个子数组的每个数字的第N 位都为0 。现在我们已经把原数组分成了两个子数组,每个子数组都包含一个只出现一次的数字,而其它数字都出现了两次。因此到此为止,所有的问题我们都已经解决。
public class Solution {
//num1,num2分别为长度为1的数组。传出参数 将num1[0],num2[0]设置为返回结果
public void FindNumsAppearOnce(int [] array,int num1[] , int num2[]) {
if (array.length < 2){
return;
}
int temp = 0;
// 将数组进行异或操作
for (int i = 0; i < array.length; i++) {
temp = temp^array[i];
}
// 找到第一个1的位置
int indedOf1 = findFistBit1(temp);
for (int i = 0; i < array.length; i++) {
// 判断是索引位置是否为1
if (isBit(array[i],indedOf1)){
num1[0]^= array[i];
}else {
num2[0]^= array[i];
}
}
}
// 求第一个为1的位置
private int findFistBit1(int num) {
int indexBit = 0;
// int型中用32位表示
while (((num&1)==0) && indexBit < 32){
// 每次比较后右移1位
num = num>>1;
indexBit++;
}
return indexBit;
}
//判断indedOf1位置是否为1
private boolean isBit(int num, int indedOf1) {
num = num >> indedOf1;
return (num & 1) == 1;
}
}
解题分析:
一个直观的思路是进行两层的for循环遍历这样时间复杂度为O(n^2),但是题目中给出了是递增有序的数组,利用这个条件是否可以进行优化时间复杂度。
以[1 2 4 7 11 15],期待和15为例,定义两指针,分别指向首和尾,那么1+15大于15因此尾部指针前进。又因为1+11<15,那么首部指针后移,这样不断的移动首尾两个指针,直至遇到所期待的和。
在题目中有一个限制条件:输出乘积最小的两数。这里就可以看作一个函数问题了,x+y的值为定值,找出xy最小的时x与y的取值,分析后可以发现,f=xy是一个开口向下的函数,只有最大值,两个数之间的距离越远其乘积越小。依据上面的取值过程刚好符合输出的是找的距离最远的两个数。
代码实现:
public ArrayList<Integer> FindNumbersWithSum(int [] array, int sum) {
ArrayList<Integer> res = new ArrayList<>();
if (array ==null || array.length == 0){
return res;
}
int left = 0,r = array.length-1;
while (left < r){
int temp = array[left]+array[r];
if (temp == sum){
//当找到值相等时便返回
res.add(array[left]);
res.add(array[r]);
break;
}else if (temp < sum){
left++;
}else {
r--;
}
}
return res;
}
解题分析:
借用上面的解题思路,可以发现利用滑动窗口的思想去解决问题,当小于目标值时窗口长度扩大,当大于目标值时窗口长度缩小。
代码实现:
//这道题目有一简单点在于其序列不是给定的,而是自然数排列的1 2 3 4...
public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
//当目标值过小时不可能存在连续数字
if (sum < 3){
return res;
}
//窗口的两侧指针,
int plow = 1,phigh = 2;
while (phigh > plow){
//连续的序列,利用求和公式:(a0+an)*n/2
int curSum = (phigh+plow) * (phigh-plow+1)/2;
if (curSum == sum){
ArrayList<Integer> temp = new ArrayList<>();
for (int i = plow; i <= phigh; i++) {
temp.add(i);
}
res.add(temp);
//添加完后窗口要前进
plow++;
}else if (curSum < sum){
//窗口内小于目标值,窗口右移
phigh++;
}else {
//窗口内大于目标值,窗口左移
plow++;
}
}
return res;
}
解题分析:
题目中是单词不变顺序翻转,利用字符串数组,以空格对其分割是比较有效的。
代码实现:
public String ReverseSentence(String str) {
//把首尾的空格去除判断是否为空,字符串的比较不要用==号
if (str.trim().equals("")){
return str;
}
String[] strs = str.split(" ");
String res = "";
for (int i = strs.length-1; i >=0 ; i--) {
res += strs[i]+" ";
}
//利用上面的那个for循环会导致结尾时多加一个空格需要删除
return res.trim();
题目分析:
一开始想的是利用位移来实现,借用了排序汇总不用交换用赋值来进行交换的方法。
代码实现:
public String LeftRotateString(String str,int n) {
if (str == null || str.length() == 0){
return str;
}
char[] arr = str.toCharArray();
int N = arr.length-1;
for (int i = 0; i < n; i++) {
char temp = arr[0];
for (int j = 0; j < N ; j++) {
arr[j] = arr[j+1];
}
arr[N] = temp;
}
return String.valueOf(arr);
}
代码优化:
从上面可以看出其时间复杂度为O(n*N)其时间复杂度难以接受。那么是否有优化的方法。
以"abcdefg"为例,左旋转2个字符,可以分别旋转ab和cdefg然后再把整体进行旋转便是想要的结果了。
代码实现:
public String LeftRotateString(String str,int n) {
if (str == null || str.length() == 0){
return str;
}
char[] arr = str.toCharArray();
reverse(arr,0,n-1);
reverse(arr,n,str.length()-1);
reverse(arr,0,str.length()-1);
return String.valueOf(arr);
}
//翻转方法的实现
private void reverse(char[] arr, int start, int end) {
while (start < end){
char temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
解题分析:
判断5个数是不是连续,最直接的方法就是去排序。因为0可以当任意数来使用,那么需要统计0的个数和排序后相邻数组的空缺,来判断是否满足连续。有一点需要注意的是当数组中出现两个相同的数字时那么一定是不连续的。
代码实现:
public boolean isContinuous(int [] numbers) {
if (numbers == null || numbers.length == 0){
return false;
}
Arrays.sort(numbers);
//记录0的个数
int zero = 0;
for (int i = 0; i < numbers.length; i++) {
if (numbers[i] == 0){
zero++;
}
}
//记录距离
int gap =0;
for (int i = zero; i < numbers.length-1; i++) {
if(numbers[i] == numbers[i+1]){
return false;
}
gap += numbers[i+1]- numbers[i]-1;
}
//根据距离和0的个数进行判断
if (gap > zero){
return false;
}
return true;
}
解题分析:
最初可以采用暴力法,用数组构造环进行解决
public int LastRemaining_Solution(int n, int m) {
if (n < 1 || m < 1) return -1;
int[] arr = new int[n];
int index = -1; //这里把index设为-1是为了陪while循环中先进行index++操作
int step = 0;//记录已经走过的数字
int count = n;//记录目前还有多少人
while (count > 0){
index++;
if (index >= n) index=0; //模拟环
if (arr[index] == -1) continue;//当已经被删除时跳过
step++;
if (step == m){
arr[index] = -1;
step = 0;//新一轮把step设为0
count--;//剩余人数--
}
}
return index;
}
这道题目就是约瑟夫环问题,在表述上稍微又不同点在于报数时是从0到m-1报数,但这个和从1到m报数是完全一样的意思,在分析的时候采用的也是从1到m的报数方法。
假设有41个人,从1开始报数,报到3时便剔除。
[0 1 2 3 4 5 ... 39 40]
第一次应该出去的索引是:(3-1)%41。因为索引是从0开始的因此要减一。剩余的为:
[0 1 3 4 5 6 ... 39 40]
因为从3开始还要报数为了和上面的情况相同,可以处理成下面的情况:
[38 39 0 1 2 ... 36 37]
每个索引减去m,再把负数的调整为正数,即加上41(因为前面的索引是在41个元素的情况下排序的,所以调整应该是加上41而不是减去一个人的总数40)。
那么将其对应回去:(2+3)%41便是对应最初始情况下的序号了。
这样不断的递归下去,得到最后的索引序号,然后再不断的向上进行返回。
根据上面可以得出一个递推的关系式:
f(n,m)=[f(n-1,m)+m]%n
代码实现:
public int LastRemaining_Solution(int n, int m) {
//当没有人参加时
if (n == 0){
return -1;
}
if (n == 1){
return 0;
}else {
return (LastRemaining_Solution(n-1,m)+m)%n;
}
}
也可以把上面代码改成迭代的形式实现
public int LastRemaining_Solution(int n, int m) {
//当没有人参加时
if (n == 0){
return -1;
}
//当只有一个人的时候,便是索引为0的位置
int index = 0;
//从只有两个人开始,不断的进行循环迭代
for (int i = 2; i <=n ; i++) {
index = (index+m)%i;
}
return index;
}
题目中的要求把常规的解法限制了,可以向位运算这些靠拢。不能用乘法,那么就正常加法;如何写终止条件是关键。
public class Solution {
public int Sum_Solution(int n) {
int sum = n;
// n>0时递归执行运算,判断是否大于0纯粹是为了方便与运算,并无其他特别含义。
// 当n==0时,只执行前面的n>0,由与运算的短路特性直接返回false
boolean ans = (n>0) && ((sum+=Sum_Solution(n-1))>0);
return sum;
}
}
举例考虑:5+17=22。可以分成三步进行:第一步只做各位相加不进位,此时相加的结果是12(个位数5和7相加不要进位是2,十位数0和1相加结果是1);第二步做进位,5+7中有进位,进位的值是10;第三步把前面两个结果加起来,12+10的结果是22,刚好5+17=22。对数字做运算,除了四则运算之外,也就只剩下位运算了。位运算是针对二进制的,我们就以二进制再来分析一下前面的三步走策略对二进制是不是也适用。5的二进制是101,17的二进制是10001。还是试着把计算分成三步第一步各位相加但不计进位,得到的结果是10100(最后一位两个数都是1,相加的结果是二进制的10。这一步不计进位,因此结果仍然是0);第二步记下进位。在这个例子中只在最后一位相加时产生一个进位,结果是二进制的10;第三步把前两步的结果相加,得到的结果是10110,转换成十进制正好是22。由此可见三步走的策略对二进制也是适用的。而对于加法操作由于二进制中只有0 1因此完全可以用异或操作代替。
public class Solution {
public int Add(int num1,int num2) {
while (num2 != 0){
int temp = num1^num2;
num2 = (num1&num2) << 1;
num1 = temp;
}
return num1;
}
}
与此类似的有不使用新的变量交换两个变量的值:
// 基于加法
a = a+b;
b = a-b;
a = a-b;
// 基于位运算
a = a^b;
b = a^b;
a = a^b;
第7章 面试案例
解题思路:
有些情况题目中是没有考虑的比如:123+12这种,题目考虑的相对来说要简单一些,只考虑符号在首元素的情况。有一个隐含的限制,题目中需要返回的是int类型数据,但是可能字符串会超出int型范围,因此在保存的时候不能直接用int来保存结果。
代码实现:
public class Solution {
public int StrToInt(String str) {
int n = str.length(),flag = 1;
long res = 0;
if (n == 0){
return 0;
}
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == '-'){
flag = -1;
} else if (str.charAt(i) == '+'){
continue;
}else if (str.charAt(i)<='9'&&str.charAt(i)>='0'){
// res += str.charAt(i)-'0';
// res *= 10;
// 利用位运算实现上面的两行代码
res = (res << 1) + (res << 3) + (str.charAt(i) & 0xf);
}else {
return 0;
}
}
// 配合前面的不用位运算使用
// res = res*flag/10;
res = res*flag;
// 还有边界要求
if (res > 2147483647 || res < -2147483648){
return 0;
}
return (int)(res*flag);
}
}
解题思路:
因为题目中限定了数字的范围寻找重复的元素,直接用hash表即可。
代码实现:
public boolean duplicate(int numbers[], int length, int[] duplication) {
//Java默认的boolean类型的数据初始值为false
boolean[] flag = new boolean[length];
//在提交的时候发现用numbers.length就会报错,因为可能会有空数组的情况
for (int i = 0; i < length; i++) {
if (flag[numbers[i]] == true){
duplication[0] = numbers[i];
return true;
}else {
flag[numbers[i]] = true;
}
}
return false;
}
7.3 构建乘积数组
解题分析:
因为无法使用除法,使用连乘则会造成时间复杂度为O(n^2)。画出乘积数组
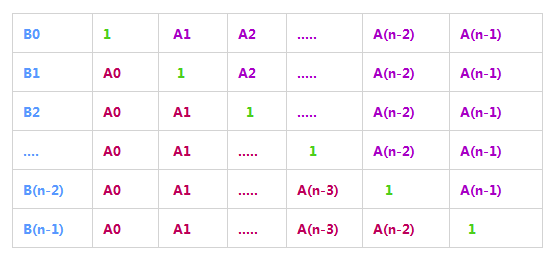
分析上图可以发现:
B[i]的左半部分和B[i-1]有关将:B[i]的左半部分乘积看成C[i],有C[i]=C[i-1]*A[i-1])
B[i]的右半部分(紫色部分)与B[i+1]有关:将B[i]的右半部分乘积看成D[i],有D[i]=D[i+1]*A[i+1])
因此我们先从0到n-1遍历,计算每个B[i]的左半部分; 然后定义一个变量temp代表右半部分的乘积,从n-1到0遍历,令B[i]*=temp,而每次的temp与上次的temp关系即为temp*=A[i+1]
代码实现:
public int[] multiply(int[] A) {
if (A == null || A.length < 2){
return null;
}
int[] B = new int[A.length];
B[0] = 1;
//先计算出所有B[i]的左半部分
for (int i = 1; i < A.length; i++) {
B[i] = B[i-1] * A[i-1];
}
//考虑右半部分,计算出B[i]的值
int temp = 1;
for (int i = A.length-2; i >= 0; i--) {
temp *= A[i+1];
B[i] *= temp;
}
return B;
}
7.4 正则表达式匹配
主要分成两种情况:下一个字符是*下一个字符不是*
public boolean match(char[] str, char[] pattern){
if(str == null || pattern == null) return false;
return judge(str,0,pattern,0);
}
private boolean judge(char[] str,int index1,char[] pattern,int index2){
//检验有效性,str从头到尾,pattern从头到尾均匹配成功
if(index1 == str.length && index2 == pattern.length)
return true;
//pattern先到尾,匹配失败
if(index1 != str.length && index2 == pattern.length)
return false;
//判断下一个字符为*的情况
if(index2+1 < pattern.length && pattern[index2+1] == '*'){
if(index1 != str.length && (pattern[index2] == str[index1] || pattern[index2] =='.'))
return judge(str,index1,pattern,index2+2)//认为*匹配0个字符
|| judge(str,index1+1,pattern,index2+2) //认为匹配str中的1个字符
|| judge(str,index1+1,pattern,index2);
else
return judge(str,index1,pattern,index2+2);
} else if(index1 != str.length){ //下一个不为*时判断当前字符是否匹配
if(str[index1] == pattern[index2] || pattern[index2] =='.')
return judge(str,index1+1,pattern,index2+1);
//若当前不匹配直接返回
return false;
}
return false;
}
7.5 表示数值的字符串
解题分析:
这两道题目就是正则表达式的使用,为了练习可以使用下面两个网站:
https://c.runoob.com/front-end/854 有较多的正则表达式例子,可以对照分析
http://tool.chinaz.com/regex/ 可以在线测试正则表达式
代码实现:
public boolean isNumeric(char[] str) {
String string = String.valueOf(str);
return string.matches("[\\+-]?[0-9]*(\\.[0-9]*)?([eE][\\+-]?[0-9]+)?");
}
7.6 字符流中第一个不重复的字符
解题分析:
本题与LeetCode387类似,但稍有区别,在于本题可以对插入的数据处理。那么便是在插入数据时,用一个数组来实现hash表,在增加数据时记录频率,在输出时读取频率即可。
代码实现:
//之所以用128定义数组是因为ASCII码一共有128个常见字符
private int[] hashtable = new int[128];
private StringBuffer s = new StringBuffer();
//Insert one char from stringstream
public void Insert(char ch) {
s.append(ch);
if (hashtable[ch] == 0){
hashtable[ch] =1;
}else {
hashtable[ch]++;
}
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce() {
for (int i = 0; i < s.length(); i++) {
if (hashtable[s.charAt(i)] == 1){
return s.charAt(i);
}
}
return '#';
}
7.7 链表中环的入口结点
本题与LeetCode 142 环形链表||是相同的
7.8 删除链表中重复的节点
本题相当于是对LeetCode 83升级,这里需要把重复的节点删除了。
非递归实现:
public ListNode deleteDuplication(ListNode pHead){
// 只有0个或1个结点,则返回
if (pHead == null || pHead.next == null){
return pHead;
}
//添加一个虚拟的头节点,防止删除需要删除头结点时另外考虑
ListNode dummyHead = new ListNode(pHead.val+1);
dummyHead.next = pHead;
ListNode pre = dummyHead;
ListNode cur = dummyHead.next;
while (cur != null){
//因为可能会有多个重复的,因此需要用whil循环
if (cur.next != null && cur.val == cur.next.val){
while (cur.next != null && cur.val == cur.next.val){
cur = cur.next;
}
//因为相邻的两个已经比较过了,所以pre要连接上不重复的部分
pre.next = cur.next;
cur = cur.next;
}else{
//当没有重复节点时正常遍历
pre = pre.next;
cur = cur.next;
}
}
return dummyHead.next;
}
递归实现:
public ListNode deleteDuplication(ListNode pHead) {
if (pHead == null || pHead.next == null) { // 只有0个或1个结点,则返回
return pHead;
}
if (pHead.val == pHead.next.val) { // 当前结点是重复结点
ListNode pNode = pHead.next;
while (pNode != null && pNode.val == pHead.val) {
// 跳过值与当前结点相同的全部结点,找到第一个与当前结点不同的结点
pNode = pNode.next;
}
return deleteDuplication(pNode); // 从第一个与当前结点不同的结点开始递归
} else { // 当前结点不是重复结点
pHead.next = deleteDuplication(pHead.next); // 保留当前结点,从下一个结点开始递归
return pHead;
}
}
7.9 二叉树的下一个节点
7.10 对称的二叉树
解题分析:
这一题和前面的镜像二叉树很相似的,可以参考镜像二叉树
代码实现:
boolean isSymmetrical(TreeNode pRoot) {
if (pRoot == null){
return true;
}
return isSymmetrical(pRoot.left,pRoot.right);
}
private boolean isSymmetrical(TreeNode left, TreeNode right) {
if (left == null && right == null){
return true;
}
if (left == null || right == null){
return false;
}
if (left.val == right.val){
return isSymmetrical(left.left,right.right)&&isSymmetrical(left.right,right.left);
}
return false;
}
7.8 二叉树的下一个节点
参考程序员代码面试指南第3章部分,借用评论区的回答,可以分为三种情况讨论:
1.二叉树为空,则返回空;
2.节点右孩子存在,则设置一个指针从该节点的右孩子出发,一直沿着指向左子结点的指针找到的叶子节点即为下一个节点;
3.节点不是根节点。如果该节点是其父节点的左孩子,则返回父节点;否则继续向上遍历其父节点的父节点,重复之前的判断,返回结果
7.9 对称的二叉树
参考LeetCode 101. 对称二叉树
7.10 按之字形顺序打印二叉树
参考LeetCode中剑指offer该题目处的讨论
//用来保存最终结果
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
helper(pRoot,0);
return res;
}
private void helper(TreeNode node,int level){
if(node == null) return;
if(res.size() == level)
res.add(new ArrayList<Integer>());
if(level%2 == 0)
//在尾部插入元素
res.get(level).add(node.val);
else
//在头部插入元素
res.get(level).add(0,node.val);
helper(node.left,level+1);
helper(node.right,level+1);
}
7.11 把二叉树打印成多行
借用上面之字形打印的代码,稍作修改。本题与LeetCode 102. 二叉树的层序遍历 题目一样
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
solve(pRoot,0);
return res;
}
private void solve(TreeNode node,int level){
if(node == null) return;
if(res.size() == level)
res.add(new ArrayList<Integer>());
res.get(level).add(node.val);
solve(node.left,level+1);
solve(node.right,level+1);
}
7.12 序列化二叉树
参考程序员代码面试指南第三章
7.13 二叉搜索树的第k个结点
采用中序遍历的方法进行记录寻找
int index = 0; //计数器
TreeNode KthNode(TreeNode pRoot, int k)
{
//中序遍历计算k
if(pRoot != null){
TreeNode node = KthNode(pRoot.left,k);
if(node != null)
return node;
index++;
if(index == k)
return pRoot;
node = KthNode(pRoot.right,k);
if(node != null)
return node;
}
return null;
}
7.14 滑动窗口的最大值
参考评论区代码,题解参考程序员代码面试指南第1章
public ArrayList<Integer> maxInWindows(int [] num, int size){
if(num == null || num.length == 0 || size <=0 || num.length < size)
return new ArrayList<Integer>();
ArrayList<Integer> res = new ArrayList<>();
//双端队列,用来记录每个窗口的最大值下标
LinkedList<Integer> qmax = new LinkedList<>();
for(int i=0;i<num.length;i++){
//peekLst查看队列的最后一个元素
while(!qmax.isEmpty() && num[qmax.peekLast()]<num[i])
qmax.pollLast();//删除队列的最后一个元素
qmax.addLast(i);//在队列尾部添加
//判断对首元素是否过期,当超过窗口大小时便弹出元素
if(qmax.peekFirst() == i-size)
qmax.pollFirst();
//向result列表中加入元素
if(i >= size-1)
res.add(num[qmax.peekFirst()]);
}
return res;
}
7.15 机器人的运动范围
7.16 剪绳子
采用动态规划,动态转移方程为:dp[i]=max(dp[j]*dp[i-ij) 0<j<i
public int cutRope(int target) {
//当target<=3时,1段位3,2段最大为2,进行列举
if(target == 2) return 1;
if(target == 3) return 2;
int[] dp = new int[target+1];
//这里记录的是最大的,因为有可能只有一段即没有剪的情况但是题目中要求必须大于1段
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
int max = 0;//记录最大乘积
for(int i=4;i<=target;i++){
//因为分成1 3段和分成3 1段结果是一样的,为了减少时间复杂度需要除以2
for(int j=1;j<=i/2;j++)
max = Math.max(max,dp[j]*dp[i-j]);
dp[i] = max;
}
return dp[target];
}
0




 本博客精选面试算法题目,涵盖基础知识、高质量代码、时间空间效率优化、面试能力培养及经典案例,解析二叉树、链表、字符串等数据结构,探讨排序、查找、递归算法,分享画图、分解问题解决技巧。
本博客精选面试算法题目,涵盖基础知识、高质量代码、时间空间效率优化、面试能力培养及经典案例,解析二叉树、链表、字符串等数据结构,探讨排序、查找、递归算法,分享画图、分解问题解决技巧。
















 615
615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








