双足机器人往复平衡行走

双足机器人通过往复躯干平衡的行走

摘要

本文展示了在五自由度（自由度）双足机器人上进行的步行测试结果。该机器人由墨西哥拉古纳技术研究所开发，采用往复质量作为平衡装置。所提出的双足步态模式基于摆线运动，以避免行走过程中脚与地面的冲击。躯干和肢体的同步运动参数使机器人保持平衡，并避免电机转矩的饱和。通过行走仿真，可在实施测试前验证零力矩点（ZMP）的合适行为。实验获得的结果最终验证了所提出行走模式的有效性。

关键词 ：双足机器人、Gait模式、ZMP、Cycloidal运动、Biped运动规划

1 引言

人形机器人在人类通常使用的环境中执行任务的应用已受到专家的广泛重视，这些机器与人类的互动已经成为现实。因此，双足运动成为人形机器人一种自然的位移方式。如果采用双足行走，则无需特殊设施即可实现这类机器人在任何地方（如医院、汽车、火车、机场等）的协作。因此，已有大量关于双足机器人的研究致力于实现稳定行走。

在多种表面、斜坡、台阶和楼梯上进行了测试。一些原型机已被用于对所提出方法的实验验证。一个名为Rabbit的平面五杆双足机器人已被用于评估与行走和奔跑、冲击分析、极限环及混杂系统相关的控制器[7, 30, 31]。具有52个自由度的机器人WEBIAN能够以0.21米/秒的速度行走[10, 26, 27]，并被用于控制算法稳定性的分析[17, 32]。此类分析已应用于具有57个自由度的ASIMO人形机器人，该机器人具备行走、奔跑、跳跃、转向以及上下楼梯的能力[12]。HRP‐2具有30个自由度和58公斤的质量[13, 16]，已在多个实验室中被广泛用于控制、运动规划以及人机交互等方面的研究。波士顿动力公司的PetMan人形机器人能够自然行走，并可完成弯曲和跳跃动作，即使在受到扰动的情况下也能保持出色的步态[24]。基本上，双足机器人的行走控制可以通过时变算法和非时变算法两种方式实现。本文研究的是采用时变算法并基于预设轨迹进行控制的双足机器人。许多学者在此领域做出了贡献；在[25]中，BLR‐G2机器人采用了针对冠状面和矢状面的解耦控制方法。在[15]中，Meltran II机器人应用了用于轨迹跟踪的PID控制。另一方面，在[19]中对一个5自由度双足机器人采用了计算力矩控制，并在[9]中报告了对一个20轴双足机器人进行力控制增强的轨迹跟踪仿真研究。其他用于轨迹跟踪控制器设计的方法则基于零力矩点（ZMP）的概念[29]，该概念常被用作行走稳定性判据[11, 13, 14, 17, 18, 23, 32]。

我们的双足机器人Bip‐ITLag采用基于摆线规律的轨迹，用于自由足和髋部在矢状面上的运动。这类运动此前已用于18个自由度的Bioloid人形机器人的三维行走[3, 22]。在其他研究中，已对Bip‐ITLag的开发进行了一些介绍[1, 2, 4–6, 20, 21, 28]。这些论文讨论了机器人在髋部固定情况下的仿真研究或初步实验分析。本文展示了Bip‐ITLag机器人首次实时行走测试所获得的结果。第2节介绍了该双足机器人的设计描述。第3节给出了描述髋部和足部指定运动的方程，第4节讨论了机器人的正向与逆向运动学方程。第5节包含了针对所提出轨迹的零力矩点计算。第6节展示了Bip‐ITLag双足机器人行走测试的结果。最后一节为结论。

2 双足机器人描述

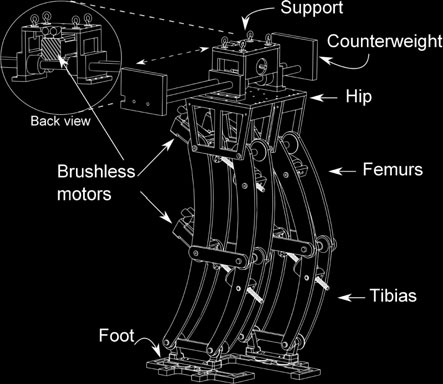
Bip‐ITLag 高 131 厘米，重 92 公斤。机器人在水平面上行走时，其位移被限制在矢状面内，以避免一个额外的自由度来控制髋部的方向；因此，该方向被约束为与支撑脚平行，如图1所示。腿部的执行器采用无刷直流电机，并通过丝杠螺母机构耦合，布置方式使得电机扭矩被放大，从而驱动胫骨和股骨同时旋转。从上述图中可以看出，躯干是一个往复质量，其在额状面上移动，以在行走过程中保持机器人的平衡。运动由一台无刷直流电机产生，并通过同步带传递至躯干。

平衡机构的设计也可在图1中看出；配重杆长度为 91.44 厘米，整个平衡机构的重量为 27.70 千克（其中框架重 8.68 千克，配重重 19.02 千克）（图 2）。

3 轨迹规划

足部和髋部运动的轨迹规划应以实现稳定行走的方式进行。本研究中应用的摆线轨迹在位移的起点和终点处具有零加速度，因此在此时刻连杆的动态力并不显著。随后，在运动过程中加速度发生平滑变化，整个机构中的主要振动载荷得以避免。这种动态力的合适行为有助于行走的稳定性。摆线轨迹基于[3, 22]中提出的方案，其中轨迹参数根据机器人的尺寸被适当选择。对于双足机器人Bip‐ITLag，这些参数必须进行调整。机器人应从一种小腿几乎垂直的姿势开始；然后，在第一步开始时，髋部向下移动，有助于减少扭矩消耗。对于双足机器人Bip‐ITlag，摆线轨迹由以下方程定义。

对于自由足

$$
x_p =
\begin{cases}
x_{pi} + s \left( \frac{t}{T_1} - \frac{1}{2\pi} \sin \frac{2\pi t}{T_1} \right), & 0 < t \leq T_1 \
x_{pi} + s, & T_1 < t \leq T
\end{cases}
$$

$$
y_p = h_p \sin \left( \frac{\pi x_p}{s} + \frac{1}{2} \pi \right), \quad 0 < t \leq T
$$

$$
\dot{x}_p =
\begin{cases}
\frac{s}{T_1} \left( 1 - \cos \frac{2\pi t}{T_1} \right), & 0 < t \leq T_1 \
0, & T_1 < t \leq T
\end{cases}
$$

$$
\dot{y}_p = \frac{h_p \pi \dot{x}_p}{s} \cos \left( \frac{\pi x_p}{s} + \frac{1}{2} \pi \right), \quad 0 < t \leq T
$$

$$
\ddot{x}_p =
\begin{cases}
\frac{2\pi s}{T_1^2} \sin \frac{2\pi t}{T_1}, & 0 < t \leq T_1 \
0, & T_1 < t \leq T
\end{cases}
$$

$$
\ddot{y}_p = \frac{h_p \pi \ddot{x}_p}{s} \cos \left( \frac{\pi x_p}{s} + \frac{1}{2} \pi \right) - \frac{h_p \pi^2 \dot{x}_p^2}{s^2} \sin \left( \frac{\pi x_p}{s} + \frac{1}{2} \pi \right), \quad 0 < t \leq T
$$

对于髋部

$$
x_c =
\begin{cases}
x_{ci} + v_c t, & 0 < t \leq T_1 \
x_{ci} + 2s, & T_1 < t \leq T
\end{cases}
$$

$$
y_c =
\begin{cases}
y_{ci} + \frac{h_c}{2} \left( \frac{2t}{T_1} - \frac{1}{2\pi} \sin \frac{4\pi t}{T_1} \right), & 0 < t \leq \frac{T_1}{2} \
y_{ci} + h_c \left( 1 - \frac{2t - T_1}{T_1} - \frac{1}{2\pi} \sin \frac{4\pi t}{T_1} \right), & \frac{T_1}{2} < t \leq T_1 \
y_{ci}, & T_1 < t \leq T
\end{cases}
$$

$$
\dot{x}_c =
\begin{cases}
v_c, & 0 < t \leq T_1 \
0, & T_1 < t \leq T
\end{cases}
$$

$$
\dot{y}_c =
\begin{cases}
\frac{2h_c}{T_1} \left( 1 - \cos \frac{4\pi t}{T_1} \right), & 0 < t \leq \frac{T_1}{2} \
-\frac{2h_c}{T_1} \left( 1 - \cos \frac{4\pi t}{T_1} \right), & \frac{T_1}{2} < t \leq T_1 \
0, & T_1 < t \leq T
\end{cases}
$$

$$
\ddot{x}_c = 0, \quad 0 < t \leq T
$$

$$
\ddot{y}_c =
\begin{cases}
\frac{8\pi h_c}{T_1^2} \sin \frac{4\pi t}{T_1}, & 0 < t \leq \frac{T_1}{2} \
-\frac{8\pi h_c}{T_1^2} \sin \frac{4\pi t}{T_1}, & \frac{T_1}{2} < t \leq T_1 \
0, & T_1 < t \leq T
\end{cases}
$$

以及用于平衡机构

$$
r_d =
\begin{cases}
r_{ini} + \Delta r_1 \left( \frac{t}{T_1} - \frac{1}{2\pi} \sin \frac{2\pi t}{T_1} \right), & 0 < t \leq T_1 \
r_{ini} + \Delta r_1 + \Delta r_2 \left( \frac{t - T_1}{T_2} - \frac{1}{2\pi} \sin \frac{2\pi (t - T_1)}{T_2} \right), & T_1 < t \leq T
\end{cases}
$$

$$
\dot{r}_d =
\begin{cases}
\frac{\Delta r_1}{T_1} \left( 1 - \cos \frac{2\pi t}{T_1} \right), & 0 < t \leq T_1 \
\frac{\Delta r_2}{T_2} \left( 1 - \cos \frac{2\pi (t - T_1)}{T_2} \right), & T_1 < t \leq T
\end{cases}
$$

$$
\ddot{r}_d =
\begin{cases}
\frac{2\pi \Delta r_1}{T_1^2} \sin \frac{2\pi t}{T_1}, & 0 < t \leq T_1 \
\frac{2\pi \Delta r_2}{T_2^2} \sin \frac{2\pi (t - T_1)}{T_2}, & T_1 < t \leq T
\end{cases}
$$

其中 $ T_2 = T - T_1 $ 表示轨迹上剩余的时间，$ e = \pm 1 $ 用于在每一步改变配重的运动方向。

前述方程使用的所有参数均在表格中进行了说明。最终参数集是通过完成多次仿真确定的，直到机器人表现出合适的行为，实现稳定行走且电机转矩无饱和现象。

参数	描述	值	单位
T	步态周期	6.0	[s]
T1	简单支撑期	3.0	[s]
s	步长	0.3	[m]
xpi	足的初始位置	−0.15	[m]
hp	足的最大高度	0.03	[m]
xci	髋部的初始X坐标	0.075	[m]
yci	髋部的初始高度	0.79	[m]
hc	髋部的最大高度	−0.01	[m]
vc = s/T	髋部速度	0.05	[m/s]
rini	配重初始位置	−0.28	[m]
Δr1	第一配重位移	0.028	[m]
Δr2	第二配重位移	0.252	[m]

4 运动学建模

本节给出了将髋部和自由足的期望运动转换为机器人关节运动所使用的方程。指定的操作坐标向量为 $ x_d = [x_c, y_c, x_p, y_p]^T $，其中 $ (x_p, y_p) $ 和 $ (x_c, y_c) $ 分别表示自由足和髋部在笛卡尔坐标中的位置，而坐标 $ (x_s, y_s) $ 表示固定在地面上的足部当前位置。所有位置均相对于图3所示框架定义。另一方面，关节变量是向量 $ q_d = [q_{d1}, q_{d2}, q_{d3}, q_{d4}]^T $ 的分量，其中 $ q_{di} $（i = 1…4）表示机器人第i个连杆的角度，如图3所示。这些关节变量决定了机器人行走过程中的瞬时姿态。图3中所示参数的值（用于定义机器人几何结构）在表2中给出。

n自由度串联机器人的正向运动学模型是一个函数，用于关联 $ q_d $ 和 $ x_d $。该函数使我们能够找到操作坐标与机器人关节变量之间的关系。
$$
x_d = f(q_d); \tag{1}
$$

对于Bip‐ITLag，其正向运动学方程由以下给出：
$$
\begin{bmatrix}
x_c \ y_c \ x_p \ y_p
\end{bmatrix}
=
\begin{bmatrix}
L(\cos(q_{d1}) + \cos(q_{d1} + q_{d2})) + x_s \
L(\sin(q_{d1}) + \sin(q_{d1} + q_{d2})) + y_s \
L(\cos(q_{d1}) + \cos(q_{d1} + q_{d2}) + (\cos(q_{d3}) + \cos(q_{d3} + q_{d4}))) + x_s \
L(\sin(q_{d1}) + \sin(q_{d1} + q_{d2}) + (\sin(q_{d3}) + \sin(q_{d3} + q_{d4}))) + y_s
\end{bmatrix}
$$

另一方面，逆向运动学可以用通用矢量方程 $ q_d = f^{-1}(x_d) $ 表示，Bip‐ITLag 的逆向运动学方程为：

$$
q_{d1} = \text{atan2} (y_c - y_s, x_c - x_s) - \frac{1}{2} e_1 \cos^{-1} \left( \frac{(x_c - x_s)^2 + (y_c - y_s)^2 - 2L^2}{2L^2} \right)
$$

$$
q_{d2} = \text{atan2} (y_c - y_s, x_c - x_s) + \frac{1}{2} e_2 \cos^{-1} \left( \frac{(x_c - x_s)^2 + (y_c - y_s)^2 - 2L^2}{2L^2} \right) - q_{d1}
$$

$$
q_{d3} = \pi - \text{atan2} (y_c - y_p, x_c - x_p) + \frac{1}{2} e_3 \cos^{-1} \left( \frac{(x_c - x_p)^2 + (y_c - y_p)^2 - 2L^2}{2L^2} \right)
$$

$$
q_{d4} = \text{atan2} (y_c - y_p, x_c - x_p) - \frac{1}{2} e_4 \cos^{-1} \left( \frac{(x_c - x_p)^2 + (y_c - y_p)^2 - 2L^2}{2L^2} \right) - q_{d3}
$$

其中
$$
e_i =
\begin{cases}
+1, & \text{Human posture (knee forward)} \
-1, & \text{Bird posture (knee backwards)}
\end{cases}
$$

现在，为了确定操作速度与关节速度之间的关系，对公式(1)求时间导数：
$$
\dot{x}_d = J(q_d)\dot{q}_d \tag{2}
$$
其中 $ J(q_d) $ 是定义的雅可比矩阵
$$
J(q_d) = \frac{\partial f(q_d)}{\partial q_d}
$$

通过从(2)式中分离出 $ \dot{q}_d $，我们确定了期望的关节速度向量：
$$
\dot{q}_d = J^{-1}(q_d)\dot{x}_d \tag{3}
$$

另一方面，对式（2）求时间导数，得到
$$
\ddot{x}_d = \dot{J}(q_d)\dot{q}_d + J(q_d)\ddot{q}_d \tag{4}
$$

最后，从（4）中解出 $ \ddot{q}_d $ 得到
$$
\ddot{q}_d = J^{-1}(q_d)[\ddot{x}_d - \dot{J}(q_d)\dot{q}_d] \tag{5}
$$
表示期望的关节加速度。

如前一节所述，对于配重，期望的位置、速度和加速度（$ r_d, \dot{r}_d, \ddot{r}_d $）直接根据摆线运动确定。

5 零力矩点作为行走稳定性判据

机器人的行走可分为两个阶段：单支撑相（SSP）和双支撑相（DSP）。当机器人迈步且仅由一只脚支撑时，处于单支撑相。双支撑相则从双脚接触地面开始，直到其中一只脚抬起为止。在行走过程中，双足机器人运动所产生的关节中的力和力矩会传递到支撑脚（或双脚）。在此脚（或双脚）上，若要保持机器人的平衡，地面反作用力必须产生所需的力和力矩。因此，地面可在支撑脚（或双脚）上施加X和Z方向的水平力矩，这些力矩由地面约束力的垂直分量所产生。该力作用的理论点被Vukobratović称为零力矩点（ZMP）[29]。因此，为了在行走过程中保持机器人平衡，必须使零力矩点位于机器人脚部的支撑多边形之内。该多边形在单支撑相时为脚印本身，在双支撑相时为脚印之间的凸区域。

对于Bip‐ITLag的行走，在摆动足开始抬起进入单支撑相（SSP）时，开始对摆动足和髋部相关变量进行轨迹跟踪控制。同时，配重保持在支撑脚同一侧，以使零力矩点（ZMP）位于对应支撑脚的支撑多边形内。当步态结束时，双支撑相（DSP）开始，支撑多边形扩大；随后通过施加一种摆线运动将配重向相反侧移动，从而保持机器人的平衡。该过程在每一步中重复执行。

Bip‐ITLag的零力矩点坐标可以表示为
$$
x_{zmp} = \frac{-sT_z - h_t f_{Tx}}{f_{Ty}} \tag{6}
$$

$$
z_{zmp} = \frac{sT_x - h_t f_{Tz}}{f_{Ty}} \tag{7}
$$

其中，$ h_t $ 表示支撑脚踝关节的高度，即从地面到支撑脚与胫骨关节的垂直距离。$ f_{Tx} $、$ f_{Ty} $ 和 $ f_{Tz} $ 分别为机器人通过这些关节作用在支撑脚上的力的x、y和z分量；$ sT_x $ 和 $ sT_z $ 分别为机器人在同一关节上施加的力矩的x和z分量。这些力和力矩是运动过程中惯性和重力效应的结果。

参数	描述	值	单位
L	连杆长度	0.40	[m]
W	连接宽度	0.21	[m]
b1, b4	胫骨弯曲角	0.1977	[rad]
b2, b3	股骨弯曲角	0.1791	[rad]
d1, d4	从胫骨螺钉关节到膝盖的距离	0.09	[m]
d2, d3	从股骨螺钉关节到髋部的距离	0.115	[m]

6 实验

双足机器人Bip‐ITLag的实验测试通过Simulink、Matlab 的 Real‐Time Windows Target工具箱实时完成。使用了两块Sensoray626 数据采集板进行控制信号的通信和施加。五个Kollmorgen S603型号驱动器与同品牌的AKM32D无刷电机配合使用。采样时间为3毫秒。

用于跟踪所提出关节轨迹的控制律是
$$
u = K_p \tanh(a\tilde{q}) + K_d \dot{\tilde{q}} + \text{Sat}\left(K_i \int \tilde{q} dt, c\right) \tag{8}
$$
其中 $ u = [\tau_1, \tau_2, \tau_3, \tau_4, f_{cp}]^T $ 是旋转和配重受力轴上的扭矩向量，
$ K_p = \text{diag}[k_{pi}] $，
$ K_d = \text{diag}[k_{di}] $，
$ K_i = \text{diag}[k_{ii}] $，
$ \tanh(#) = [\tanh(#_1), \tanh(#_2), \dots, \tanh(#_n)] $，
此外 $ \text{Sat}(m) = [\text{sat}(m_1), \text{sat}(m_2), \dots, \text{sat}(m_n)] $，
其中 $ \text{sat}_i(m_i) = \text{sign}(m_i)\min(|m_i|, c_i) $。

控制器的参数和增益在表3中定义。

控制器	a	kp	kd	ki	c
τ1 胫骨 1	1	110	2	35	100
τ2 股骨 1	1	100	2	20	90
τ3 股骨 2	1	100	2	20	90
τ4 胫骨 2	1	100	2	30	90
fcp 配重	300	40	25	1	30

用于实现实验行走的轨迹参数是在前一节中通过仿真和零力矩点计算获得的。所采用的步行周期为6秒（单支撑相3秒，双支撑相3秒），可使机器人获得最佳稳定性。测试过程中供给电机的控制信号如图5、6和7所示。

在测试过程中，机器人行走时的一系列姿态如图8所示。初始姿态下，后足为左脚，配重位于右侧，因此第一步由左脚完成。当第一步结束时，进入双支撑相起点，随后配重移至左侧，以在下一步中保持机器人平衡。机器人行走过程的视频可在[8]中查看。

7 结论

本文介绍了双足机器人Bip‐ITLag在实时条件下的步行测试结果。该机器人由墨西哥拉古纳理工学院机电与控制实验室设计和制造。机器人的行走模式基于自由足和髋部的摆线轨迹，以避免行走过程中的冲击和显著的振动载荷。用于机器人行走的参数是通过仿真研究并应用零力矩点（ZMP）作为稳定性准则预先确定的。实现行走所采用的控制方法为饱和PID控制。根据施加的扭矩所获得的结果，提出以下方案是可行的：更快的行走。然而，我们将脚部力传感器的前期集成用于真实的零力矩点线性反馈视为未来的工作，以便获得更可靠的控制方案。