广义执行-评价学习在智能家居能源管理中的应用

智能家居能源管理中的广义执行‐评价学习最优控制

摘要

本文研究一种新的广义执行‐评价学习最优控制方法，旨在实现智能家居系统的最优能量控制与管理，以期最小化家庭用户的消费成本。在所提出的广义执行‐评价学习最优控制方法中，首次建立了全局迭代、局部迭代和内部迭代三个迭代过程，以求得最优能量控制律。该方法的主要贡献在于：针对周期时变系统，基于每次迭代中的控制律序列（而非单一控制律），构建了自适应动态规划（ADP）中值迭代和策略迭代的通用迭代结构，并同时加快了收敛速度。本文证明了广义执行‐评价学习最优控制方法下迭代值函数的单调性、收敛性和最优性。最后，通过数值结果和对比分析展示了所提出方法的优越性。

索引词

自适应评价设计，自适应动态规划，近似动态规划，执行‐评价学习，能源管理，智能电网，最优控制。

一、引言

SMART 家庭微电网作为一种智能电网的新颖且先进的范式，是通过能源与信息网络基础设施的深度融合而提出的，涉及传统集中式发电、自动化控制系统、智能计算、智能管理系统等[1]–[5]。随着电力存储设备的快速发展，储能管理在智能微电网系统中发挥着重要作用[6]–[8]。电力存储设备不仅能够在电力供应大于负载需求时储存多余的电能，还可在电力供应成本较高时满足负荷需求。因此，电力存储设备的最优运行是一种为家庭用户节约电能消耗的重要技术。另一方面，值得注意的是，智能家居中的实时负荷需求和电价通常无法建立其机理模型，这使得采用传统的基于模型的最优控制方法设计电力存储设备的最优控制律几乎不可能[9]–[12]。

这一挑战推动了针对智能家居系统中能源的学习与智能最优控制研究。

自适应动态规划（ADP）结合最优控制、神经网络和强化学习，已成为非线性系统[13]–[17]的一种显著的类脑学习最优控制方法。2013年，一种基于时间的 Q‐学习（TBQL）算法[18],被首次提出，用于实现智能家居系统中储能设备的最优能量管理。考虑到太阳能和风能资源，根据TBQL算法[19],[20]获得了智能家居的最优能量控制。

由于基于值迭代的自适应动态规划算法[21]无法保证系统状态在迭代控制律下的收敛性，文献[22],中开发了一种基于策略迭代的自适应动态规划算法，但在每次迭代中都需要求解一个广义贝尔曼方程。通常，广义贝尔曼方程也难以求解，这限制了基于策略迭代的自适应动态规划算法的应用。如何在自适应动态规划中结合值迭代和策略迭代，是获取智能家居系统最优能量控制律所必需的技术，这也促使了我们的研究。

本文提出了一种基于自适应动态规划（ADP）技术的新型广义执行‐评价学习（GACL）最优控制方法，用于实现智能家居系统的最优能量管理。这是首次分别建立全局迭代、局部迭代和内部迭代三个迭代过程，以获得最优能量控制律。本文所开发的GACL方法具有三个主要贡献：第一，该方法针对周期性时变系统，基于每次迭代中的控制律序列（而非单一控制律），在自适应动态规划（ADP）中为值迭代和策略迭代建立了统一的迭代结构；第二，证明了所开发的GACL方法的收敛性，确保在迭代控制律下，迭代值函数能够收敛至最优值；第三，与传统ADP算法相比，所开发的GACL方法加快了收敛速度。最后，通过一个数值例子展示了广义执行‐评价学习的应用结果。

II. 预备知识与问题描述

智能家居系统由电网、用户的负荷需求和储能设备组成。本文中采用电池作为储能设备。 展示了智能家居系统的结构，其中储能设备可分别设计为“充电模式”、“空闲模式”和“放电模式”。在此情况下，如何优化储能设备的控制律是降低智能家居系统成本的关键。

在[18],[23],[24],中描述了储能设备的动态特性，本文也采用了该模型。对于时间 t= 0,1,…，设 Bt和 Tt分别为储能设备的能量存储量和功率输出，则储能设备的模型表示为 Bt+1= Bt−Tt×η(Tt)，其中我们令 Tt> 0和Tt< 0分别表示储能设备的放电和充电状态。令 Tt= 0表示储能设备处于空闲状态。设储能设备充放电效率[18],[23],[24]表示为 η(Tt) = 0.898 − 0.173|Tt|/Trate, 其中 Trate> 0为储能设备的额定功率输出。

受[21],值函数（其期望最小化）的启发，被表示为
$$
\sum_{t=0}^{\infty} \gamma^t(\alpha_1(E_tP_t)^2 + \alpha_2(B_t - B_o)^2 + \alpha_3T_t^2),
$$
其中 Et为实时电价， Pt为来自电网的总电功率， Bo表示能量存储的中间限值。值函数中第一项(EtPt)²的物理意义是最小化总成本。第二项(Bt − Bo)²旨在使电池的储能接近存储限值的中间值，从而避免电池的完全充放电功率。第三项 T²t 用于防止电池出现过大的充放电功率。因此，第二项和第三项的目标是延长电池寿命。参数 α1、 α2和 α3是这三个项的权重。通常， α1、 α2和 α3是根据优化需求人为设定的参数。令 0< γ< 1为折扣因子，用于方便数学计算并避免值函数出现无限或无穷小的情况。

设x1,t= Pt和x2,t= Bt−Bo为系统状态。令ut= Tt为系统的控制量。根据负荷平衡[21]以及储能设备的模型，系统函数可表示为
$$
x_{t+1} = F(x_t, u_t, t) = \left( \begin{array}{c} Z_t - u_t \ x_{2,t} - u_t\eta(u_t) \end{array} \right),
$$
其中 xt=[x1,t, x2,t]T和 Zt表示用户的负荷需求。令 ωt=（ut， ut+1，…），值函数可表示为
$$
V(x_0, \omega_0, 0) = \sum_{t=0}^{\infty} \gamma^tH(x_t, u_t, t),
$$
其中效用函数定义为 H(xt, ut, t)。最优值函数可以定义为
$$
V^*(x_t, t) = \inf_{\omega_t} {V(x_t, \omega_t, t)}.
$$

III. 广义执行‐评价学习最优控制方法

在本节中，提出了一种新的广义执行‐评价学习最优控制方法，以通过特性分析获得智能家居系统的最优控制律。

A. 广义执行-评价学习最优控制方法的推导

由(2)和(3)可知，负荷需求和电价均为时变参数，这导致最优值函数随时间变化。对于一般用户而言，负荷需求和电价是周期函数。

假设1： 负荷需求 Zt和电价Et均为周期为 Θ= 24小时的周期函数。

根据假设1，负荷需求和电价满足 Zt = Zt+Θ , Et = Et+Θ。受[22],中对 k ∈{0,Θ, 2Θ,…}的启发，定义一个新的效用函数为
$$
\Psi(x_k , A_k) = \sum_{\theta=0}^{\Theta-1} \gamma^\Theta H(x_{k+\theta}, u_{k+\theta}, \theta).
$$
最优性能指标函数中的最优 Q型值函数[21]可以表示为
$$
J^ (x_k, A_k) = \Psi(x_k, A_k) + \vartheta \min_{A_{k+\Theta}} J^ (x_{k+\Theta}, A_{k+\Theta}),
$$
其中定义为 ϑ= γΘ。最优控制律序列可表示为 U∗(xk) = arg min Ak {J∗(xk, Ak)}.

基于上述准备工作，可以引入广义执行‐评价学习最优控制方法。

首先，我们定义 N={N1,N2,…} 为正整数集合，使得对于任意 i= 1, 2,…, Ni> 0 均为正整数。令 i= 0, 1,… 为全局迭代索引。设 U0(xk) 为初始控制律，使得
$$
J_0(x_k, A_k) = \Psi(x_k, A_k) + \vartheta J_0(x_{k+\Theta}, U_0(x_{k+\Theta})),
$$
其中 J0(xk, Ak)是初始值函数。对于 i= 1，迭代控制律序列 U1(xk)可通过以下方式计算
$$
U_1(x_k) = \arg \min_{A_k} J_0(x_k, A_k).
$$
然后，对于 i= 1, 2,…，全局迭代在之间进行
$$
J_i(x_k, A_k) = \Psi(x_k, A_k) + \vartheta J_i(x_{k+\Theta}, U_i(x_{k+\Theta})),
$$
and
$$
U_{i+1}(x_k) = \arg \min_{A_k} J_i(x_k, A_k).
$$

注释1: 全局迭代过程确保了所开发的算法的收敛性。首先，给定计算精度 ε> 0。然后，利用全局迭代索引i= 1, 2,…，迭代成本函数可更新为(9)。如果|Ji(xk, k) − Ji−1(xk, k)| ≤ ε，则算法收敛。否则，令 i= i+1，继续迭代。

第二次迭代过程是局部迭代。对于 i= 1，以及局部迭代索引 j1= 0, 1,…,N1−1，迭代成本函数可以更新为
$$
J_{1,j1+1}(x_k, A_k) = \Psi(x_k, A_k) + \vartheta J_{1,j1}(x_{k+\Theta}, U_1(x_{k+\Theta})),
$$
其中 J1,0(xk, Ak) = J0(xk, Ak) ∀xk, Ak。定义J1(xk, Ak) = J1,N1(xk, Ak)。对于 i= 2, 3,…，迭代控制律序列为
$$
U_i(x_k) = \arg \min_{A_k} J_{i-1}(x_k, A_k).
$$
令Ji,0(xk, Ak) = Ji−1(xk, Ak)，对于 ji= 0, 1,…,Ni, Ni ∈N，迭代成本函数通过以下方式更新
$$
J_{i,ji+1}(x_k, A_k) = \Psi(x_k, A_k) + \vartheta J_{i,ji}(x_{k+\Theta}, U_i(x_{k+\Theta})),
$$
其中我们定义
$$
J_i(x_k, A_k) = J_{i,Ni}(x_k, A_k).
$$

声明指出，迭代控制律序列 Ui(xk)，i= 0,1,…无法通过直接求解(8)和(12)获得，因为 Ui(xk)是一个迭代控制律序列。因此，引入一种新的内部迭代来构造该序列。

对于 i= 0，1，…，令 li = 0，1，…，Θ − 1为内层迭代索引。根据(3)，对于 li = 0，1，…，Θ−1，我们定义一个新系统为
$$
x_{k+1} = F(x_k, u_k, l_i) = \left( \begin{array}{c} Z_{\Theta-1-li} - u_k \ x_{2,k} - u_k \end{array} \right).
$$
对于 li = 0, 1,…,Θ −1，我们令
$$
U(x_k, u_k, l_i) = x_k^T H_{\Theta-1-li} x_k + \alpha_3 u_k^2,
$$
where HΘ−1−li=[ α1(EΘ−1−li)² 0; 0 α2]. 对于 i= 1,2,…，我们定义一个新的内部迭代成本函数为 Vi li(xk)。对于 i= 1, 2,…和 li= 0，我们定义
$$
V_0^i(x_k) = J_{o,i-1}(x_k, U_{i-1}(x_k)),
$$
其中，对于 i= 1，令 Jo,i−1(xk, U0(xk)) = J0(xk, U0(xk))；对于i= 2,3,…，令 Jo,i−1(xk, Ui−1(xk)) =Ji−1,Ni−1−1(xk, Ui−1(xk)). 然后，对于 i= 1, 2,…和 li= 0, 1,…,Θ −1，可得到内层迭代控制律
$$
v_{li}^i(x_k) = \arg \min_{u_k} {U(x_k, u_k, li) + \gamma V_{li}^i(x_{k+1})},
$$
其中 xk+1= F(xk, uk, li)在(15)中定义，效用函数 U(xk, uk, li)在(16)中定义。然后，内层迭代代价函数计算为
$$
V_{li+1}^i(x_k) = U(x_k, v_{li}^i(x_k), li) + \gamma V_{li}^i(F(x_k, v_{li}^i(x_k), li)).
$$
对于 i= 0，1，…，可以构造迭代控制律序列 Ui(xk)
$$
U_i(x_k) = {v_{\Theta-1}(x_k), v_{\Theta-2}^i(x_k), …, v_{i0}(x_k)}.
$$
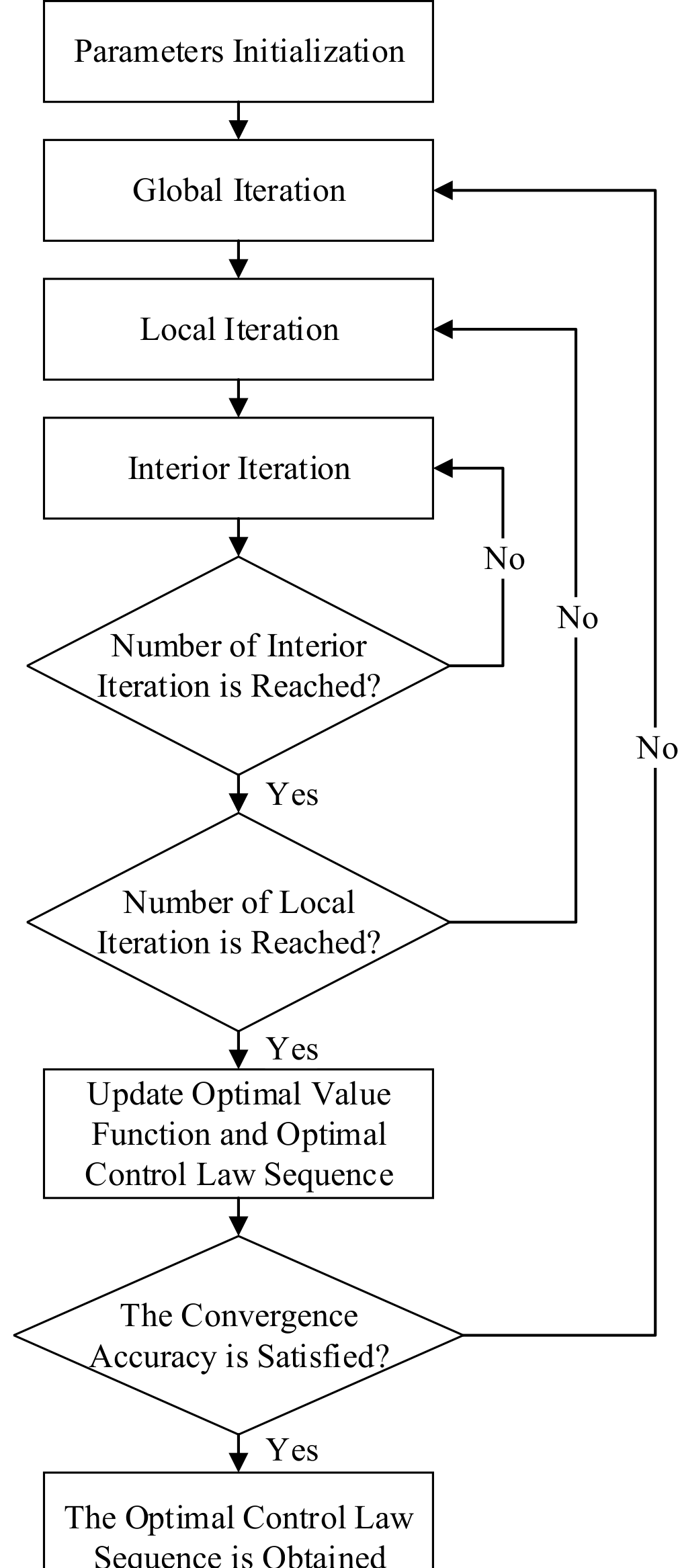
所开发的算法的迭代过程如 所示。

B. 广义执行-评价学习最优控制方法的性质

在本小节中，对广义Actor‐Critic学习最优控制方法的性质进行了分析。首先，给出了内部迭代的性质。

定理 1： 对于 i= 0, 1,…，定义迭代控制律序列 Ui(xk) 如 (20) 所示，其中 v i 获得，则 Ui(xk) 满足 (8) 对于 i= 1 以及 (12) 对于 i= 2, 3,…。

证明： 采用数学归纳法来证明该陈述。首先，对于 i= 0, 1,…，我们定义
$$
\Psi(x_k, U_i(x_k)) = \sum_{l_i=0}^{\Theta-1} \gamma^{l_i} U(x_k, v_{l_i})
$$
对于 i= 1和 l1 = 0，我们知道 V₀¹(xk) = J₀(xk, U₀(xk)) , 其中 U₀(xk)是一个给定的控制律序列。然后，我们可以通过求解得到控制律 v₀¹(xk)
$$
v_0^1(x_k) = \arg \min_{u_k} {U(x_k, u_k, 0) + \gamma V_0^i(x_{k+1})},
$$
其中 xk+1 = F(xk, uk, 0)。对于任意 l₁ = 0,1,…,Θ−1，我们可以得到
$$
V_{l_1+1}^1(x_k) = U(x_k, v_{l_1}, l_1) + \gamma V_{l_1}
= \min_{u_k} {U(x_k, u_k, l_1) + \gamma V_{l_1}
= \min_{u_k} {U(x_k, u_k, l_1)
+ \gamma \min_{u_{k+1}} {U(x_{k+1}, u_{k+1}, l_1 - 1)
+ · · · + \gamma \min_{u_{k+l_1}} {U(x_{k+1}, u_{k+l_1}, 0)
+ \gamma V_0^1(x_{k+l_1+1})} · · ·}.
$$

IV. 数值结果

本节旨在通过一个数值例子来说明广义执行‐评价学习最优控制方法的性能。该数值例子中的负荷需求（千瓦）和实时电价（美分）选自[18]–[20]。负荷需求和实时电价在168小时（一周）内的变化分别如 168小时的住宅负荷需求。(b) 平均住宅负荷需求。(c) 168小时的实时电价。(d) 平均电价。)和 168小时的住宅负荷需求。(b) 平均住宅负荷需求。(c) 168小时的实时电价。(d) 平均电价。)所示。实际上，电价由政府或电力市场确定。本文所选取的负荷需求和相应电价仅用于研究目的，不会影响本文的理论研究。可以看出，负荷需求和电价均为周期为Θ= 24的类周期函数。负荷需求和电价的平均值分别如 168小时的住宅负荷需求。(b) 平均住宅负荷需求。(c) 168小时的实时电价。(d) 平均电价。)和 168小时的住宅负荷需求。(b) 平均住宅负荷需求。(c) 168小时的实时电价。(d) 平均电价。)所示。

备注2： 在假设1中，负荷需求 Zt和电价 Et均被假定为周期函数。因此，本文可以证明所开发算法的最优性。然而，如果周末负荷需求变化过大，则不能直接使用所开发的算法对一周的控制进行优化。在这种情况下，可以通过分别考虑工作日和周末来使用所开发的算法。此外，需要注意的是，数值实验中采用的负荷需求是 168小时的住宅负荷需求。(b) 平均住宅负荷需求。(c) 168小时的实时电价。(d) 平均电价。)所示的原始负荷需求数据，而不是平均数据。因此，此处的负荷需求设置是合理的。

储能设备的参数设置如下。根据常见储能设备的参数，设定储能设备的容量为100千瓦时，即 Bo = 50 kWh。设备的额定功率设为16.5 kW。设备的初始能量设为60千瓦时。定义价值函数如式(1)所示，其中我们分别设置 α₁ = 1、α₂ = 0.5和 α₃ = 0.2。初始状态随机设定为 x₀ = [8, 60]ᵀ。实现广义执行‐评价学习最优控制方法需要一个初始控制律 U₀(xk)。通常，初始控制律可根据经验设计。当负荷需求和电价均明显较低时（例如午夜时段），让设备充电；当负荷需求和电价费率明显较高的时段，例如晚餐时间。其他时间设备的充放电类型则任意选择。基于上述实验，我们可以设计如所示的初始控制律序列。

我们实现了所提出的广义Actor‐Critic学习最优控制方法，进行了 i= 20次全局迭代，以展示迭代值函数 Ji(xk)的特性，其中在每次局部迭代中，对于 i= 1, 2,…，我们将 Ni设计为任意正整数，用于局部迭代 j= 0, 1,…, Ni。迭代值函数 Ji(xk, Ui(xk))的变化情况如所示。从可以看出，在一天中的每个小时，迭代值函数单调不增并最终收敛至最优，验证了理论结果的正确性。

智能家居系统的最优控制显示在中。我们可以看到，当负荷需求和电价较低时设备充电，负荷需求和电价较高时设备放电。每小时的详细充放电功率也已获得，在中明显优于初始控制律。

负荷需求的最优能量管理如所示。可以看出，当负荷需求和电价较高时，电网几乎停止向负荷供电，所有功率由储能设备提供。当负荷需求和电价较低时，电网承担从电网到负荷的全部功率。储能设备中相应的能量如所示。

为了展示所开发的广义Actor‐Critic学习最优控制方法的优越性，采用了两种 Q‐学习算法，即基于时间的 Q‐学习（TBQL）算法[18]和对偶迭代 Q‐学习（Dual‐QL）算法[21]。需要注意的是，TBQL方法和Dual‐QL方法均为典型的ADP方法，已有效应用于智能能源系统。对于TBQL算法中的时间 t= 0, 1,…，控制律被更新以满足以下最优性方程 Q(xt−1, ut−1, t − 1) = H(xt, ut, t)+ Q(xt, ut, t)，其中效用函数 H(xt, ut, t) 的定义与(3)中相同。 t= 0的初始 Q函数设为零。对于 i= 0, 1, …, 对偶迭代Q‐学习算法[21]中的迭代过程表示为 Qi+1(xk,Uk) =Ψ(xk, Uk) + ϑ minUk+Θ Qi(xk+Θ,Uk+Θ)，其中初始 Q函数选择为 Q0(xk,Uk) ≡ 0。现在，对TBQL执行200次迭代，并对双Q学习算法执行30次迭代，以保证迭代值函数的收敛性。三种方法的成本比较如表I所示，其中“GIC” 表示“全局收敛迭代次数”。

原始方法	TBQL	对偶‐QL	GACL
总成本（美分）	4124.13	2877.63	2797.86
节约		30.22%	32.16%
GIC		200	30
时间（秒）		96.04	1374.24

对于TBQL算法[18], ，由于每次迭代的控制无法保证最小化迭代值函数，因此无法证明收敛值函数的最优性，在比较中表现为最差节约。而对于对偶‐QL[21]和所开发的GACL最优控制方法，迭代值函数的收敛性和最优性均已得到证明。从表I可以看出，所开发的GACL方法相比标准控制将系统运行成本降低了32.30%。与TBQL算法相比，其性能提升了2.08%，相较于对偶‐QL算法提升了0.14%。尽管所开发的GACL算法在经济节约方面的改进似乎并未明显优于对偶‐QL算法，但应注意的是，对偶‐QL方法已被有效应用于智能能源系统，因此该改进仍值得提及。另一方面，对于TBQL算法，需要200次迭代使迭代值函数收敛。对于对偶‐QL算法[21],，也需要30次全局迭代来保证其收敛性和最优性性质。然而，从可以看出，广义执行‐评价学习最优控制方法仅需5次全局迭代即可使迭代值函数收敛至最优。此外，我们还比较了收敛所需的时间。在实验中，使用联想90N900AFCP计算机，收敛时间的结果如表I所示。TBQL算法需要96.04秒使迭代值函数收敛，对偶‐QL算法需要1374.24秒使迭代值函数收敛，而GACL算法仅需64.14秒。因此，所提出的GACL算法大大减少了收敛时间，这些算法在收敛时间上存在较大差异的原因在于前两种算法需要大量的神经网络训练过程。因此，所提出的GACL算法具有更少的全局收敛迭代次数和更短的收敛时间。由此可见，所提出的广义执行‐评价学习最优控制方法的优越性得以验证。

注释3: 本文中，所开发的GACL方法使智能家居能源管理系统能够基于负荷需求和实时电价的数据实现自学习，而无需系统的数学模型，这是所开发方法的优势之一。因此，无需满足马尔可夫决策过程。通常，电力负荷需求呈周期性变化。在所开发的GACL算法的推导过程中，需确保负荷需求和电价为周期函数。需要注意的是，GACL方法是离线实现的，这是所开发算法的缺点。

五、结论

本文提出了一种新颖的广义执行‐评价学习（GACL）最优控制方法。该方法的核心思想是通过自适应动态规划（ADP）为智能家居系统寻找最优能量控制律。结合值迭代与策略迭代ADP技术，广义执行‐评价学习最优控制方法为智能家居能源管理提供了一种通用的迭代结构。广义执行‐评价学习最优控制方法中的三种迭代过程，即全局迭代、局部迭代和内部迭代，均已给出。同时证明了迭代成本函数单调不增并收敛至最优值函数。最后，通过数值结果和对比展示了所开发的算法的优越性。

在未来的工作中，我们将在本研究的基础上考虑更多实际因素，构建更真实的家庭能源管理系统模型，收集更多相关数据并进行更深入的研究，使本文的研究成果具有更高的实际应用价值。