453. Minimum Moves to Equal Array Elements_grandyang 453 minimum moves to equal array element-优快云博客

本文探讨了LeetCode题目453“最少移动次数使数组元素相等”的三种解法，包括暴力破解法、数学法及讨论区提供的高效解法。通过分析不同方法的时间和空间复杂度，帮助读者理解最优解背后的数学原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

453. Minimum Moves to Equal Array Elements

方法1: brute force
- Complexity
方法2:
- 易错点
- Complexity
方法3: math

Given a non-empty integer array of size n, find the minimum number of moves required to make all array elements equal, where a move is incrementing n - 1 elements by 1.

Example:

Input:
[1,2,3]

Output:
3

Explanation:
Only three moves are needed (remember each move increments two elements):

[1,2,3]  =>  [2,3,3]  =>  [3,4,3]  =>  [4,4,4]

方法1: brute force

官方题解： https://leetcode.com/problems/minimum-moves-to-equal-array-elements/solution/

思路：

每次为了赶上mx，我们将除了mx的所有n - 1个值+1。那么每次记录当前最大值和最小值，只要循环直到最大==最小，可以结束。

Complexity

Time complexity : O(n^2 k), where n is the length of the array and k is the difference between maximum element and minimum element.
Space complexity : O(1). No extra space required.

方法2:

discussion：https://leetcode.com/problems/minimum-moves-to-equal-array-elements/discuss/93817/It-is-a-math-question
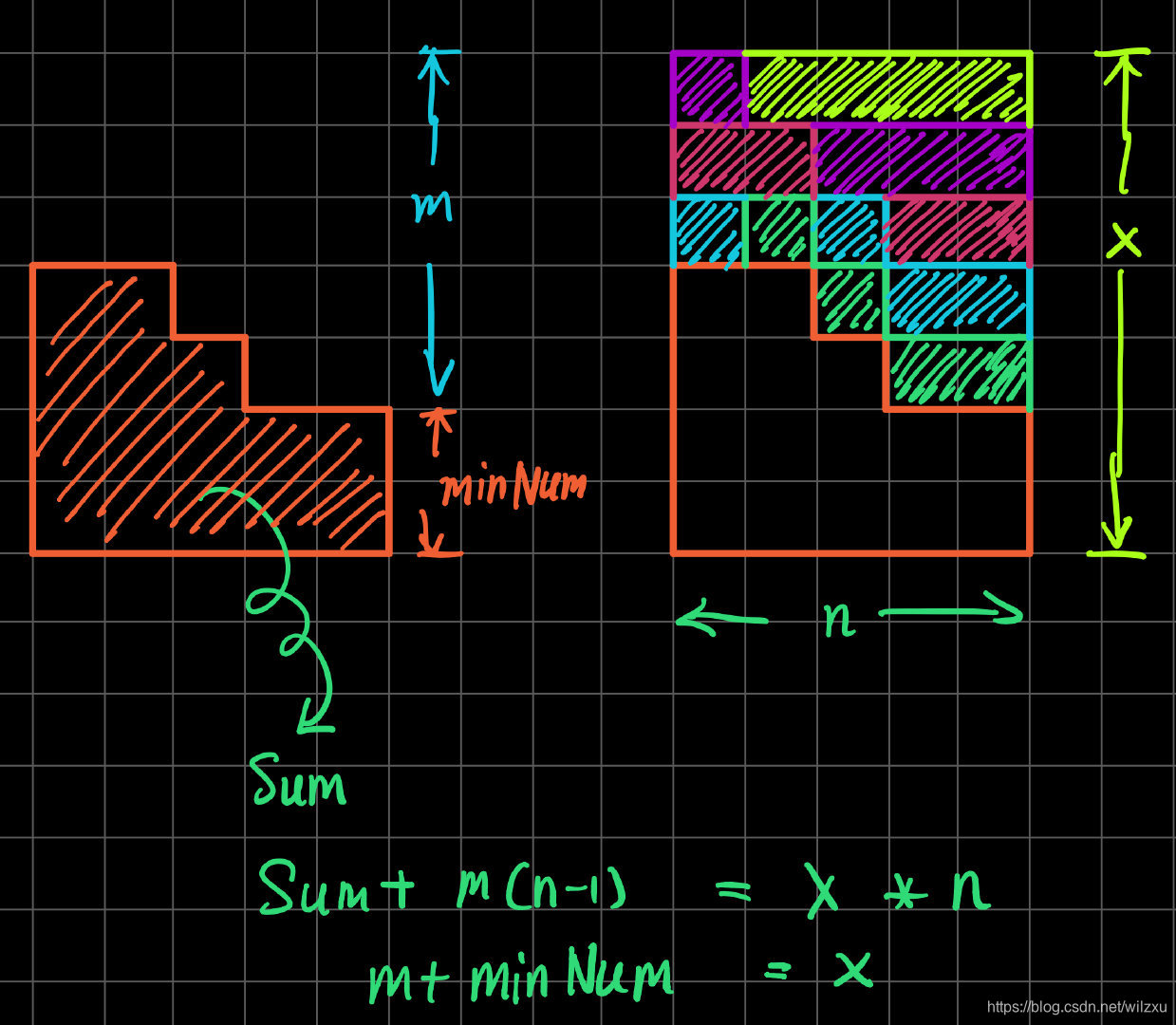
思路：

如图。

易错点

不用long会overflow
在这里插入图片描述

class Solution {
public:
    int minMoves(vector<int>& nums) {
        int mn = INT_MAX;
        long sum = 0;
        for (int num: nums){
            mn = min(mn, num);
            sum += num;
        }
        return sum - mn * nums.size();
    }
};

Complexity

Time complexity : O(n). We traverse the complete array once.
Space complexity : O(1). No extra space required.

方法3: math

grandyang: http://www.cnblogs.com/grandyang/p/6053827.html

思路：

将n - 1个++相当于将最大值–。那么每一次move都相当于从最大值-1。一共需要减多少次才能全部相等？首先全部相等的时候一定全部等于最小值，因为没有必要更小。那么只要先求出最小，然后计算每个num和最小值之间的差值，累计下来就是moves。

class Solution {
public:
    int minMoves(vector<int>& nums) {
        int mn = *min_element(nums.begin(), nums.end());
        int result = 0;
        for (int num: nums){
            result += (num - mn);
        }
        return result;
    }
};