207. Course Schedule

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:

Input: 2, [[1,0]] 
Output: true
Explanation: There are a total of 2 courses to take. 
             To take course 1 you should have finished course 0. So it is possible.

Example 2:

Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
             To take course 1 you should have finished course 0, and to take course 0 you should
             also have finished course 1. So it is impossible.

Note:

1. The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
2. You may assume that there are no duplicate edges in the input prerequisites.
3. There are several ways to represent a graph. For example, the input prerequisites is a graph represented by a list of edges. Is this graph representation appropriate?
   Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort. https://www.coursera.org/specializations/algorithms
   Topological sort could also be done via BFS.

方法1: bfs

basketking: https://www.youtube.com/watch?v=zkTOIVUdW-I
思路：

根据hint，这道题的本质是探测有向图中是否有环，如果有环课程之间互相依赖，无法完成。如果没有环，按照拓扑排序即可上完所有课程。

因此这道题可以用bfs或者dfs完成。用一个向量来记录每一门课的入度，将入度为0的课推入队列。每次出队的时候将遍历所有它的后续课程并入度-1， 如果该课程入度变成0，则推入队列。入度初始化由遍历数组并建立map/vector来完成（这里每门课是int，不需要用hash，vector就可以）。直到遍历结束，队列为空，如果有节点的入度不为零，说明存在cycle，无法上完所有课，返回false。

需要的数据结构：

1. vector<vector<int>> graph : 用来标示有向图，graph[1] : {2, 3} ，1是2,3 的先修课
2. vector<int> : 每门课的入度
3. queue<int>: 用来bfs遍历图

易错点：

1. 为什么需要最后把入度再扫一遍：因为如果有相互dependency的话，谁也不会是0。

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses, vector<int>());
        vector<int> degree(numCourses, 0);
        queue<int> q;
        vector<bool> visited(numCourses, false);
        // 建立graph，注意先修课是a[1], [c1, prereq], [c2, prereq], [c3, prereq] ->{prereq: c1, c2, c3}
        for (auto pair: prerequisites) {
            graph[pair[1]].push_back(pair[0]);
            degree[pair[0]]++;
        }
       
        // 推进所有入度为零（不需要先修课）的课程
        for (int i = 0; i < numCourses; i++) {
            if (degree[i] == 0) {
                q.push(i);
            }
        }
        
        // 遍历
        while (!q.empty()) {
            int top = q.front();
            q.pop();
            
            for (auto a: graph[top]) {
                if (--degree[a] == 0) {
                    if (visited[a]) return false;
                    visited[a] = true;
                    q.push(a);
                }
            }
        }
        
        // 检查是否还有入度不为零的课
        for (auto d: degree) if (d) return false;
        return true;
    }
};

方法2: dfs

huahua: https://www.youtube.com/watch?v=M6SBePBMznU

思路：

需要的数据结构：

1. vector<vector> graph: 用来记录先修课
2. vector<int> visited: 用来在dfs中标记status，0 = unvisited, 1 = visiting, 2 = visited
   

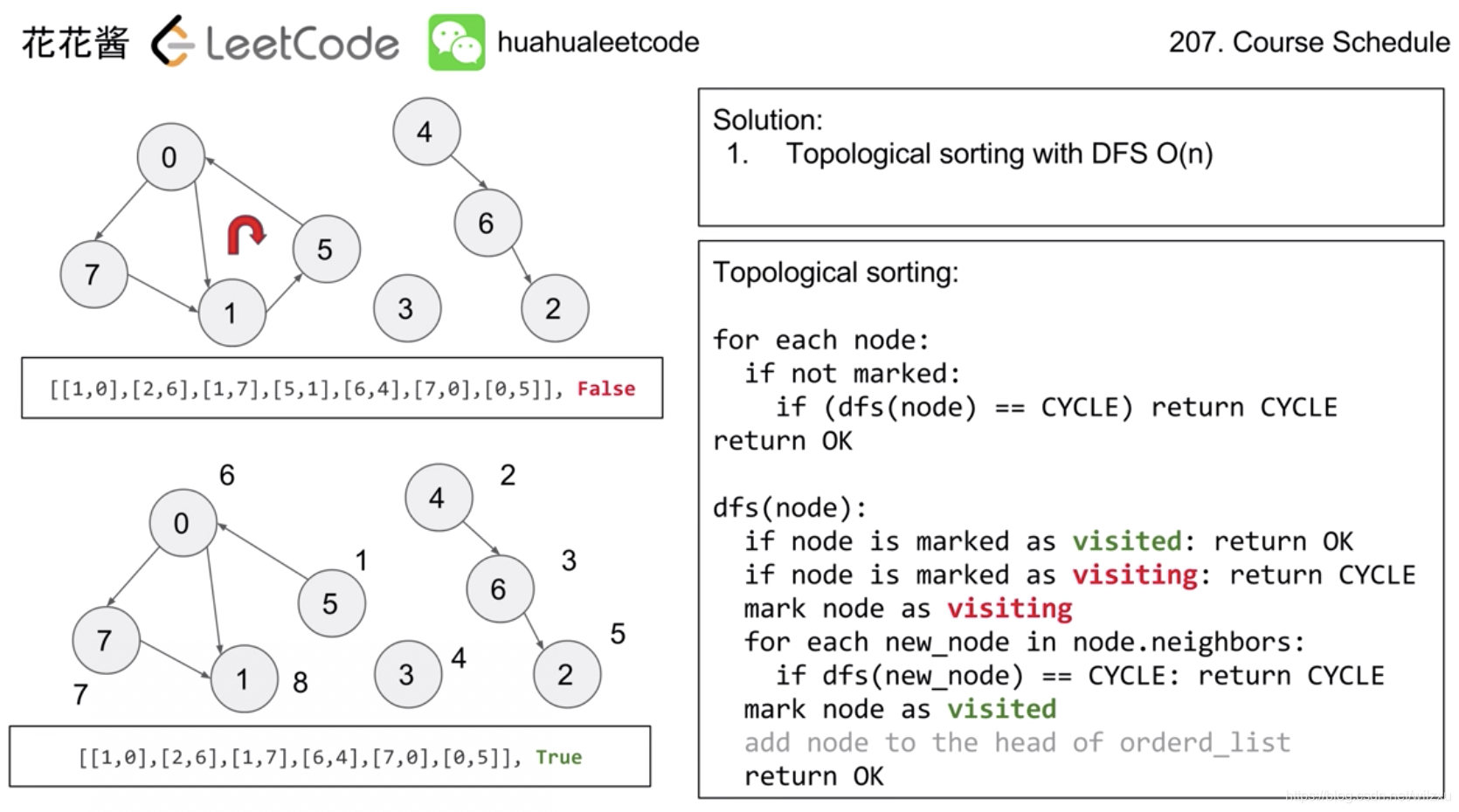
知识点： Topological order

Complexity

时间： O(n)

思路:

用dfs检测是否存在环，参考CLRS中拓扑排序的方式。与一般dfs不同的是需要设置三种状态，0 = unvisited, 1 = visiting, 2 = visited。只有当一个节点的所有子节点都遍历过，我们才将该节点标记为2，第一次遇到该节点，将其由0 变成1，所有节点初始化为0。

可以想象成一个栈来维持visiting的节点，当子节点都遍历过，我们将节点转移到visited的序列。这个visited的序列是按照修课的相反顺序，reverse之后就会得到一个topological ordered list。

易错点：

1. 要遍历所有节点发起dfs，考虑到有孤立节点
2. 注意bool的含义，这种解法标示的是“dfs中是否存在环”，主函数返回的是“能否完成所有课程”，意义相反
3. 进入dfs前将visited[i] = 1, 遍历子节点结束后visited[i] = 2
4. 注意这里被标记为visited的顺序与拓扑排序的顺序相反，后修课会先被visitied
5. dfs循环中，任意一轮循环返回的是true，都要直接返回true

class Solution {
public:
    bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {
        vector<vector<int>> graph(numCourses, vector<int>(0));
        vector<int> visited(numCourses, 0);
        
        for (auto a: prerequisites){
            graph[a.second].push_back(a.first);
        }
        
        for (int i = 0; i < numCourses; i++){
            // dfs 用来判断是否有环，或者t/f反过来代表是否能继续进行
            if (dfs(i, graph, visited)) return false;
        }
        
        return true;
    }
    
    bool dfs(int i, vector<vector<int>>& graph, vector<int> & visited ){
        if (visited[i] == 1) return true;
        if (visited[i] == 2) return false;
        
        visited[i] = 1;
        for (auto j: graph[i]){
            if (dfs(j, graph, visited)) return true;
        }
        visited[i] = 2;
        
        return false;
    }
};