Levenshtein's eidit distance

最新推荐文章于 2024-08-21 11:02:33 发布

原创最新推荐文章于 2024-08-21 11:02:33 发布 · 588 阅读

0 ·

CC 4.0 BY-SA版权

D&A 同时被 2 个专栏收录

21 篇文章

订阅专栏

Java

11 篇文章

订阅专栏

本文介绍如何使用Java实现Levenshtein距离算法，包括递归和动态规划两种方式，详细解释了算法原理及代码实现。

From Wiki, the definition of Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is equal to the number of single-character edits required to change one word into the other.

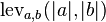Mathematically, the Levenshtein distance between two strings $a, b$ is given by $\operatorname{lev}_{a,b}(|a|,|b|)$ where

$\qquad\operatorname{lev}_{a,b}(i,j) = \begin{cases} 0 &, i=j=0 \\ i &, j = 0 \text{ and } i > 0 \\ j &, i = 0 \text{ and } j > 0 \\ \min \begin{cases} \operatorname{lev}_{a,b}(i-1,j) + 1 \\ \operatorname{lev}_{a,b}(i,j-1) + 1 \\ \operatorname{lev}_{a,b}(i-1,j-1) + [a_i \neq b_j] \end{cases} &, \text{ else} \end{cases}$

Note that the first element in the minimum corresponds to deletion(from $a$ to $b$ ), the second to insertion and the third to match or mismatch, depending on whether the respective symbols are the same.

Below is an implementation in java.

package test.LevenshteinDistance;

public class LevenshteinDistance {

	/**
	 * @param args
	 */
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		String s = "kitten";
		String t = "sitting";
		
		LevenshteinDistance ld = new LevenshteinDistance();
		
		//int recurlen = ld.recurLevenDistance(s, t);
		int dynlen = ld.dynLevenDistance(s, t);
		//System.out.println("The length is : " + recurlen);
		System.out.println("The length is : " + dynlen);
		System.out.println(s.length());
	}
	
	/*public int minimum(int a, int b, int c){
		return Math.min(Math.min(a, b), c);
	}*/
	
	public int minimum(int a, int b, int c){
		if(a < b && a < c) return a;
		if(b < a && b < c) return b;
		return c;
	}
	
	// compute the distance use recursive way
	public int recurLevenDistance(String s, String t){
		int slen = s.length();
		int tlen = t.length();
		
		int ins = 0; // for recording insert length
		int del = 0; // for recording delete length
		int sub = 0; // for substitution length
		
		if(slen == 0 && tlen == 0) return 0;
		if(slen == 0) return tlen;
		if(tlen == 0) return slen;
		
		/*if(s.charAt(slen - 1) == t.charAt(tlen - 1)){
			sub = recurLevenDistance(s.substring(0, slen - 1), t.substring(0, tlen - 1));
		}
		else{
			sub = recurLevenDistance(s.substring(0, slen - 1), t.substring(0, tlen - 1)) + 1;
		}*/
		
		sub = recurLevenDistance(s.substring(0, slen - 1), t.substring(0, tlen - 1)) 
				+ ((s.charAt(slen - 1) == t.charAt(tlen - 1)) ? 0 : 1);
		
		ins = recurLevenDistance(s.substring(0, slen - 1), t) + 1;
		del = recurLevenDistance(s, t.substring(0, tlen - 1)) + 1;
		
		return minimum(ins, del, sub);
	}
	
	// compute the distance use dynamic way
	public int dynLevenDistance(String s, String t){
		int[][] distance = new int[s.length() + 1][t.length() + 1];
		
		int i, j;
		for(i = 0; i <= s.length(); i++)
			distance[i][0] = i;
		for(j = 0; j <= t.length(); j++)
			distance[0][j] = j;
		
		for(i = 1; i <= s.length(); i++){
			for(j = 1; j <= t.length(); j++){
				distance[i][j] = minimum(distance[i - 1][j] + 1,
						distance[i][j - 1] + 1,
						distance[i - 1][j - 1] + ((s.charAt(i - 1) == t.charAt(j - 1)) ? 0 : 1));
			}
		}
		
		return distance[s.length()][t.length()];
	}
}