之前我们的超平面都是假设训练样本都是线性可分的,但是这样的假设不成立的话呢,也就是对于当前训练集,找不到一个线性可分的超平面。
对于这种情况,我们都是题将样本从原始映射到一个更高维的特征空间,使得样本在这个特征空间内 线性可分。并且,如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
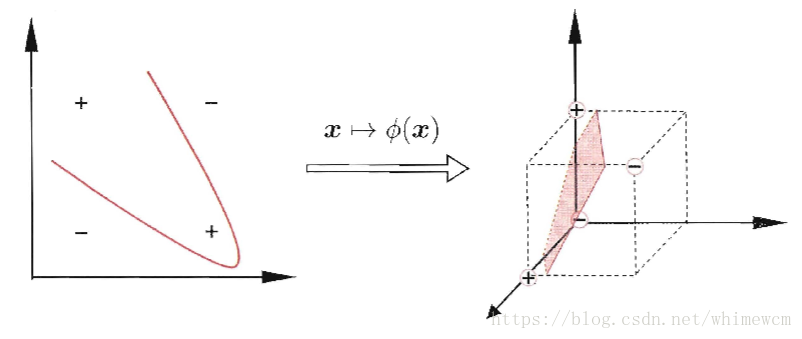

由于很难去计算样本 Xi ,Xj 映射到特征空间之后的内积
![]()
我们将问题转化为,存在一个函数

κ(. ,.)称为核函数。

半正定矩阵指的是该矩阵的各个特征向量对应的特征值非负。
所以选择合适的核函数很关键。

此外,通过函数组合得到的也是核函数。
![]()
![]()
![]()





 当训练样本无法通过线性超平面区分时,本文介绍了一种将数据映射到高维空间的方法,使其变得线性可分。通过使用核函数避免了直接计算高维空间中样本的内积,简化了复杂度。
当训练样本无法通过线性超平面区分时,本文介绍了一种将数据映射到高维空间的方法,使其变得线性可分。通过使用核函数避免了直接计算高维空间中样本的内积,简化了复杂度。
















 1416
1416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








