前言:公式理解及推导参考自《机器学习》周志华 P101
BP网络
BP网络一般是指由 误差逆传播(error BackPropagation, BP)算法训练的多层前馈神经网络。
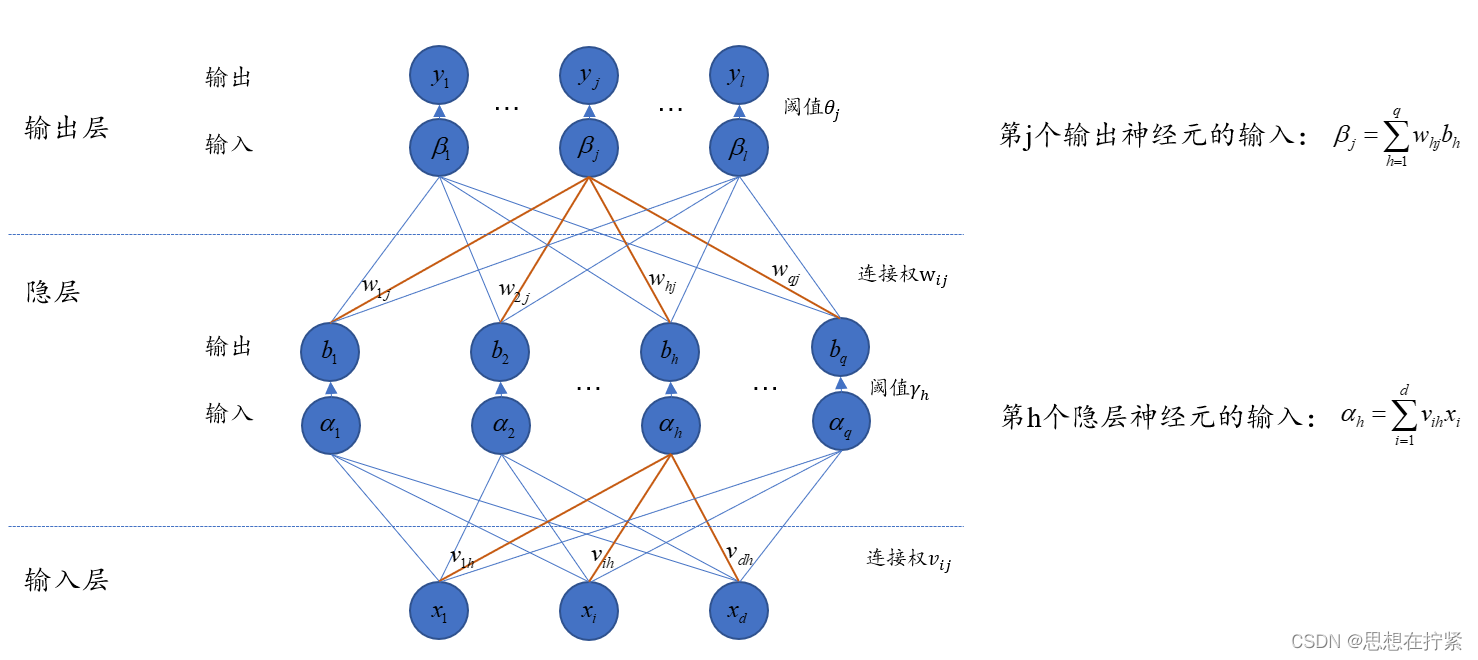
给定训练集 D = { ( x 1 , y 1 ) D=\left\{\left(\boldsymbol{x}_1, \boldsymbol{y}_1\right)\right. D={(x1,y1), ( x 2 , y 2 ) , … , ( x m , y m ) } , x i ∈ R d , y i ∈ R l \left.\left(\boldsymbol{x}_2, \boldsymbol{y}_2\right), \ldots,\left(\boldsymbol{x}_m, \boldsymbol{y}_m\right)\right\}, \boldsymbol{x}_i \in \mathbb{R}^d, \boldsymbol{y}_i \in \mathbb{R}^l (x2,y2),…,(xm,ym)},xi∈Rd,yi∈Rl,即输入示例由 d d d 个属性描述,输出 l l l 维实值向量。如下图所示,给出一个拥有 d d d 个输入神经元、 l l l 个输出神经元、 q q q 个隐层神经元的多层前馈网络结构。
对训练例 ( x k , y k ) , k ∈ ( 1 , m ) \left(\boldsymbol{x}_k, \boldsymbol{y}_k\right), k∈(1, m) (xk,yk),k∈(1,m),假定神经网终的输出为 y ^ k = ( y ^ 1 k , y ^ 2 k , … , y ^ l k ) \hat{\boldsymbol{y}}_k=\left(\hat{y}_1^k, \hat{y}_2^k, \ldots, \hat{y}_l^k\right) y^k=(y^1k,y^2k,…,y^lk),即 y ^ j k = f ( β j − θ j ) \hat{y}_j^k=f\left(\beta_j-\theta_j\right) y^jk=f(βj−θj)。关于 y ^ j k \hat{y}_j^k y^jk 的表达式来源于 MP 神经元模型,简单来说,当总输入超过阈值则输出一个信号,当总输入低于阈值会输出另一个信号。
网络在 ( x k , y k ) , k ∈ ( 1 , m ) \left(\boldsymbol{x}_k, \boldsymbol{y}_k\right), k∈(1, m) (xk,yk),k∈(1,m) 上的均方误差为 E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2} \sum_{j=1}^l\left(\hat{y}_j^k-y_j^k\right)^2 Ek=21∑j=1l(y^jk−yjk)2,此处 1/2 是为了后面求导方便。
参数更新式
网络中有
(
d
+
l
+
1
)
q
+
l
(d+l+1) q+l
(d+l+1)q+l 个参数需确定:输入层到隐层的
d
×
q
d \times q
d×q 个连接权、隐层到输出层的
q
×
l
q \times l
q×l 个连接权、
q
q
q 个隐层神经元的阈值、
l
l
l 个输出层神 经元的阈值。以隐层到输出层的连接权
w
h
j
w_{hj}
whj 为例分析参数更新,
w
h
j
w_{hj}
whj 参数更新估计式为:
w
h
j
′
=
w
h
j
+
Δ
v
=
w
h
j
−
η
∂
E
k
∂
w
h
j
w_{hj}'=w_{hj}+ \Delta v = w_{hj}-\eta \frac{\partial E_k}{\partial w_{hj}}
whj′=whj+Δv=whj−η∂whj∂Ek
其中,
η
∈
(
0
,
1
)
\eta \in (0, 1)
η∈(0,1),成为学习率(learning rate)。
因为每次更新只考虑一个参数,所以
E
k
E_k
Ek 可视为关于
w
h
j
w_{hj}
whj 的一元函数。若
∂
E
k
∂
w
h
j
\frac{\partial E_k}{\partial w_{hj}}
∂whj∂Ek 为正值,说明
w
h
j
w_{hj}
whj 越大,
E
k
E_k
Ek 越大,为使
E
k
E_k
Ek 尽可能小,所以应减去这个正的导数;若
∂
E
k
∂
w
h
j
\frac{\partial E_k}{\partial w_{hj}}
∂whj∂Ek 为负值,说明
w
h
j
w_{hj}
whj 越大,
E
k
E_k
Ek 越小,为使
E
k
E_k
Ek 尽可能小,所以应减去这个负的导数,增大
w
h
j
w_{hj}
whj。
计算导数–链式法则
注意到
w
h
j
w_{h j}
whj 先影响到第
j
j
j 个输出层神经元的输入值
β
j
\beta_j
βj,再影响到其输出值
y
^
j
k
\hat{y}_j^k
y^jk,然后影响到
E
k
E_k
Ek,有:
∂
E
k
∂
w
h
j
=
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
⋅
∂
β
j
∂
w
h
j
.
\frac{\partial E_k}{\partial w_{h j}}=\frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{h j}} .
∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj.
根据定义
β
j
=
∑
h
=
1
q
w
h
j
b
h
\beta_j = \sum_{h=1}^q w_{h j} b_h
βj=∑h=1qwhjbh ,有
∂
β
j
∂
w
h
j
=
b
h
\frac{\partial \beta_j}{\partial w_{h j}}=b_h
∂whj∂βj=bh
计算
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \frac{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}}{\partial \beta_{\mathrm{j}}}
∂y^jk∂Ek⋅∂βj∂y^jk:
=
∂
E
k
∂
y
^
j
k
⋅
∂
[
f
(
β
j
−
θ
j
)
]
∂
β
j
=
∂
E
k
∂
y
^
j
k
⋅
f
′
(
β
j
−
θ
j
)
=
∂
E
k
∂
y
^
j
k
⋅
f
(
β
j
−
θ
j
)
×
[
1
−
f
(
β
j
−
θ
j
)
]
=
∂
E
k
∂
y
^
k
k
⋅
y
^
j
k
(
1
−
y
^
j
k
)
=
∂
[
1
2
∑
j
=
1
1
(
y
^
j
k
−
y
j
k
)
2
]
∂
y
^
j
k
⋅
y
^
j
k
(
1
−
y
^
j
k
)
=
1
2
×
2
(
y
^
j
k
−
y
^
j
k
)
×
1
×
y
^
j
k
(
1
−
y
^
j
k
)
=
(
y
^
j
k
−
y
^
j
k
)
y
^
j
k
(
1
−
y
^
j
k
)
=\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathbf{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \frac{\partial\left[\mathrm{f}\left(\beta_{\mathrm{j}}-\theta_{\mathrm{j}}\right)\right]}{\partial \beta_{\mathrm{j}}}=\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \mathrm{f}^{\prime}\left(\beta_{\mathrm{j}}-\theta_{\mathrm{j}}\right)=\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \mathrm{f}\left(\beta_{\mathrm{j}}-\theta_{\mathrm{j}}\right) \times\left[1-\mathrm{f}\left(\beta_{\mathrm{j}}-\theta_{\mathrm{j}}\right)\right] = \frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathrm{y}}_{\mathrm{k}}^{\mathrm{k}}} \cdot \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\left(1-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right) \\ =\frac{\partial\left[\frac{1}{2} \sum_{\mathrm{j}=1}^1\left(\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}-\mathrm{y}_{\mathrm{j}}^{\mathrm{k}}\right)^2\right]}{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\left(1-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right)=\frac{1}{2} \times 2\left(\hat{y}_{\mathrm{j}}^{\mathrm{k}}-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right) \times 1 \times \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\left(1-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right)=\left(\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right) \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\left(1-\hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}\right)
=∂y^jk∂Ek⋅∂βj∂[f(βj−θj)]=∂y^jk∂Ek⋅f′(βj−θj)=∂y^jk∂Ek⋅f(βj−θj)×[1−f(βj−θj)]=∂y^kk∂Ek⋅y^jk(1−y^jk)=∂y^jk∂[21∑j=11(y^jk−yjk)2]⋅y^jk(1−y^jk)=21×2(y^jk−y^jk)×1×y^jk(1−y^jk)=(y^jk−y^jk)y^jk(1−y^jk)
上式计算 f ′ ( β j − θ j ) \mathrm{f}^{\prime}\left(\beta_{\mathrm{j}}-\theta_{\mathrm{j}}\right) f′(βj−θj) 时,涉及 Sigmoid 函数 f ( x ) f(x) f(x) 的导数: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f^{\prime}(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
再令
g
j
=
−
∂
E
k
∂
β
j
=
−
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
g_j=-\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \beta_{\mathrm{j}}}=-\frac{\partial \mathrm{E}_{\mathrm{k}}}{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}} \cdot \frac{\partial \hat{\mathrm{y}}_{\mathrm{j}}^{\mathrm{k}}}{\partial \beta_{\mathrm{j}}}
gj=−∂βj∂Ek=−∂y^jk∂Ek⋅∂βj∂y^jk
综上,得到关于
w
h
j
w_{hj}
whj 的更新公式为:
Δ
w
h
j
=
−
η
∂
E
k
∂
w
h
j
=
−
η
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
⋅
∂
β
j
∂
w
h
j
=
−
η
(
−
g
j
)
b
h
=
η
g
j
b
h
\Delta w_{hj} =-\eta \frac{\partial E_k}{\partial w_{hj}}=-\eta \frac{\partial E_k}{\partial \hat{y}_j^k} \cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{h j}}= -\eta (-g_j) b_h= \eta g_j b_h
Δwhj=−η∂whj∂Ek=−η∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj=−η(−gj)bh=ηgjbh
同理可得
θ
j
\theta_j
θj、
v
i
h
v_{ih}
vih、
γ
h
\gamma_h
γh 的更新公式。需注意的是,在计算过程中,确定链式求导公式是关键。
补充
f
(
x
)
=
1
1
+
e
−
x
f(x)=\frac{1}{1+e^{-x}}
f(x)=1+e−x1 的导数:
f
′
(
x
)
=
e
−
x
(
1
+
e
−
x
)
2
=
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
−
1
(
1
+
e
−
x
)
2
=
f
(
x
)
−
(
f
(
x
)
)
2
=
f
(
x
)
[
1
−
f
(
x
)
]
f'(x)=\frac{e^{-x}}{(1+e^{-x})^2} = \frac{1+e^{-x}-1}{(1+e^{-x})^2}= {\frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^2}}=f(x)-(f(x))^2=f(x)[1-f(x)]
f′(x)=(1+e−x)2e−x=(1+e−x)21+e−x−1=1+e−x1−(1+e−x)21=f(x)−(f(x))2=f(x)[1−f(x)]
参考文章:
梯度下降的参数更新公式是如何确定的? - 老董的回答 - 知乎





















 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








