文本相似性计算之编辑距离详解
概述:
编辑距离(Edit Distance):是一个度量两个字符序列之间差异的字符串度量标准,两个单词之间的编辑距离是将一个单词转换为另一个单词所需的单字符编辑(插入、删除或替换)的最小数量。一般来说,编辑距离越小,两个串的相似度越大。
编辑距离是1965年由苏联数学家Vladimir Levenshtein发明的。Levenshtein Distance也被称为编辑距离(Edit Distance)。
一、Levenshtein.distance(str1, str2);
计算编辑距离(也称Levenshtein距离) 。算法实现:动态规划
定义:
对于两个字符串a、b,长度分别为|a|、|b|,它们的Levenshtein Distance为:

i和j分别表示字符串a和字符串b的下标。下标从1开始。
例如将kitten-字转成sitting: (kitten’和’sitting’的编辑距离为3) .

相似度=1-编辑距离/Math.Max(str1.length,str2.length)=1-3/7=0.571
运算过程:
建立一个矩阵,用来存储上一步计算好的距离
- 建立一个矩阵,用来存储上一步计算好的距离
matrix_ed=np.zeros((len(str_a)+1,len(str_b)+1),dtype=np.int)
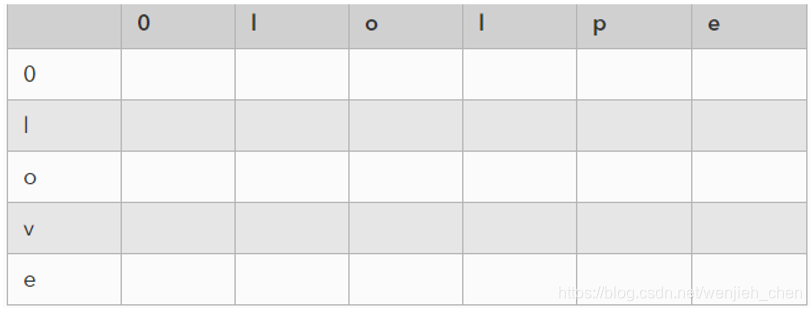
- 初始化第一行和第一列所有的距离。即:

matrix_ed[0]=np.arange(len(str_b)+1)
matrix_ed[:,0] = np.arange(len(str_a) + 1)

- 开始循环计算所有的距离,直到最后一个字符。例如:
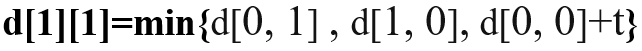

<





 本文详细介绍了编辑距离(Levenshtein Distance)的概念及其计算方法,包括动态规划实现,同时还讨论了汉明距离、莱文斯坦比、Jaro距离和Jaro-Winkler距离。这些距离度量在字符串相似度比较中有广泛应用,尤其适用于单词匹配和文本相似性分析。文章通过实例展示了不同距离计算的细节和特点,并指出Jaro-Winkler距离对前缀匹配给予更多权重,适合于单词匹配场景。
本文详细介绍了编辑距离(Levenshtein Distance)的概念及其计算方法,包括动态规划实现,同时还讨论了汉明距离、莱文斯坦比、Jaro距离和Jaro-Winkler距离。这些距离度量在字符串相似度比较中有广泛应用,尤其适用于单词匹配和文本相似性分析。文章通过实例展示了不同距离计算的细节和特点,并指出Jaro-Winkler距离对前缀匹配给予更多权重,适合于单词匹配场景。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 778
778

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








