title: “统计学知识”
author: “”
date: “2018年2月27日”
output: word_document
knitr::opts_chunk$set(echo = TRUE)
总结统计学中基础知识,以原理叙述为主。
数据度量
集中趋势的度量
- 分类数据—众数(mode):一组数据中出现次数最多的变量值。
- 顺序数据—中位数:一组数据排序后处于中间位置上的变量值。
- 顺序数据—四分位数:一组数据排序后处于25%和75%位置上的值。
- 数值数据—平均数:分为简单平均数、加权平均数等,不赘~
- 众数、中位数和平均数的关系
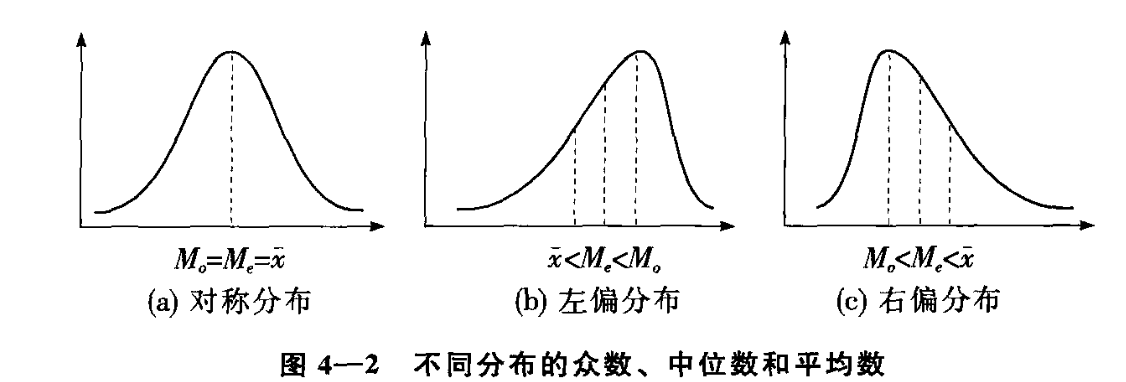
离散程度的度量
- 分类数据—异众比率:非众数组的频数占总频数的比例
- 顺序数据—四分位差:上下四分位数的差。
- 数值型数据—极差、方差、标准差:不赘。
偏态和峰态的度量
- 偏态(skewness):是对数据分布对称性的测度,对称分布则偏态系数等于0,明显不等于0表名非对称的。大于0表示右偏(定义存在歧义,上图中的右偏,有的地方称之为左偏)。
- 峰态(kurtosis):是对数据分布平峰或者尖峰程度的测度,标准正态分布峰态系数为0,大于0为尖峰分布,数据分布更集中,反之扁平分布。
## 概率论
条件概率
P ( A ∣ B ) = P ( A B ) P ( B ) P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} P(A∣B)=P(B)P(AB)
全概率公式
P ( B ) = ∑ i = 1 n P ( A i B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P\left( B \right) = \sum\limits_{i = 1}^n {P\left( {{A_i}B} \right)} = \sum\limits_{i = 1}^n {P\left( {{A_i}} \right)} P\left( {B|{A_i}} \right) P(B)=i=1∑nP(AiB)=i=1∑nP(Ai)P(B∣Ai)
贝叶斯公式
P ( A i ∣ B ) = P ( A i B ) P ( B ) = P ( A i ) P ( B ∣ A i ) ∑ j = 1 n P ( A j ) P ( B ∣ A i ) P\left( {{A_i}|B} \right) = \frac{{P\left( {{A_i}B} \right)}}{{P\left( B \right)}} = \frac{{P\left( {{A_i}} \right)P\left( {B|{A_i}} \right)}}{{\sum\limits_{j = 1}^n {P\left( {{A_j}} \right)} P\left( {B|{A_i}} \right)}} P(Ai∣B)=P(B)P(AiB)=j=1∑nP(Aj)P(B∣Ai)P(Ai)P(B∣Ai)
三大分布
正态分布
X
∼
N
(
μ
,
σ
2
)
X \sim N\left( {\mu ,{\sigma ^2}} \right)
X∼N(μ,σ2):随机变量
X
X
X服从均值为
μ
\mu
μ、方差为
σ
2
{\sigma ^2}
σ2的正态分布。其中
μ
\mu
μ决定图形的中心位置,
σ
\sigma
σ决定图形中峰的陡峭程度。
σ
\sigma
σ越大图形越平缓,反之陡峭(陡峭意为分布集中,所以方差小)。密度函数如下:
f
(
x
)
=
1
σ
2
π
exp
(
−
1
2
σ
2
(
x
−
μ
)
2
)
f\left( x \right) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( { - \frac{1}{{2{\sigma ^2}}}{{\left( {x - \mu } \right)}^2}} \right)
f(x)=σ2π1exp(−2σ21(x−μ)2)
卡方分布
设随机变量 X 1 , X 2 , … , X n {X_1},{X_2}, \ldots ,{X_n} X1,X2,…,Xn相互独立,且 X i {X_i} Xi服从标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),则随机变量的平方和$\sum\limits_{i = 1}^n {X_i^2} 服 从 自 由 度 为 服从自由度为 服从自由度为n 的 的 的{\chi ^2} 分 布 。 自 由 度 为 分布。 自由度为 分布。自由度为n 的 的 的{\chi ^2} 分 布 数 学 期 望 为 分布数学期望为 分布数学期望为n$,方差为 2 n 2n 2n
t分布
t分布也称为学生氏分布。设随机变量
X
∼
N
(
0
,
1
)
,
Y
∼
χ
2
(
n
)
X \sim N\left( {0,1} \right),Y \sim {\chi ^2}\left( n \right)
X∼N(0,1),Y∼χ2(n),且
X
X
X与
Y
Y
Y独立,则
t
=
X
Y
/
n
t = \frac{X}{{\sqrt {Y/n} }}
t=Y/nX
该分布为
t
t
t分布。
F分布
设随机变量
Y
Y
Y与
Z
Z
Z相互独立,且
Y
Y
Y和
Z
Z
Z分别服从自由度为
m
m
m和
n
n
n的
χ
2
\chi ^2
χ2分布,随机变量
X
X
X有如下表达式;
X
=
Y
/
m
Z
/
n
=
n
Y
m
Z
X = \frac{{Y/m}}{{Z/n}} = \frac{{nY}}{{mZ}}
X=Z/nY/m=mZnY
则称
X
X
X服从第一自由度为
m
m
m,第二自由度为
n
n
n的
F
F
F分布,即为
F
(
m
,
n
)
F(m,n)
F(m,n),简记为
X
∼
F
(
m
,
n
)
X \sim F\left( {m,n} \right)
X∼F(m,n)
大数定律和中心极限定理
大数定律
讨论的是在什么条件下,随机变量序列的算术平均值依概率收敛到其均值(期望)的算数平均。
即随机变量
X
n
{X_n}
Xn满足:
lim
n
→
∞
P
{
∣
1
n
∑
i
=
1
n
X
i
−
1
n
∑
i
=
1
n
E
(
X
i
)
∣
<
ε
}
=
1
,
f
o
r
∀
ε
>
0
\mathop {\lim }\limits_{n \to \infty } \;P\left\{ {\left| {\frac{1}{n}\sum\limits_{i = 1}^n {{X_i} - \frac{1}{n}\sum\limits_{i = 1}^n {E\left( {{X_i}} \right)} } } \right| < \varepsilon } \right\} = 1,for\;\forall \varepsilon > 0
n→∞limP{∣∣∣∣∣n1i=1∑nXi−n1i=1∑nE(Xi)∣∣∣∣∣<ε}=1,for∀ε>0
中心极限定理
研究随机变量和的极限分布在什么条件下为正态分布。如林德伯格-莱维中心极限定理:
设
{
X
n
}
\{X_n\}
{Xn}是独立同分布的随机变量序列,且
E
X
i
=
μ
E{X_i}=\mu
EXi=μ,
V
a
r
(
X
i
)
=
σ
2
Var(X_i)={\sigma}^2
Var(Xi)=σ2存在,则当
n
n
n足够大时,
∑
i
=
1
n
X
i
\sum\limits_{i = 1}^n {{X_i}}
i=1∑nXi近似服从
N
(
n
μ
,
n
σ
2
)
N(n\mu,n\sigma^2)
N(nμ,nσ2)。
简单的统计推断
P值
当原假设为真时所得到的样本观察结果或者更极端结果出现的概率。
假设检验
基本思想为小概率反证法,流程为:先提出原假设,再用适当的统计方法确定假设成立的可能性大小(P值),如果可能性小(小于事先设定的显著性水平),则认为原假设不成立,这里只能说明现有数据不能支撑原假设,但是不能说明备注假设成立。
列联表分析
研究两个类别型变量之间是否独立的方法。原假设为两变量独立,通常通过构建列联表进行计算分析。
简单叙述原理:原假设两个类别型变量是独立的,那么可以通过边际概率的乘积,计算独立时各种组合发生的概率,继而求出所谓的期望频数,如果期望频数和实际频数相差很大,则认为独立。贴个书上的例子:
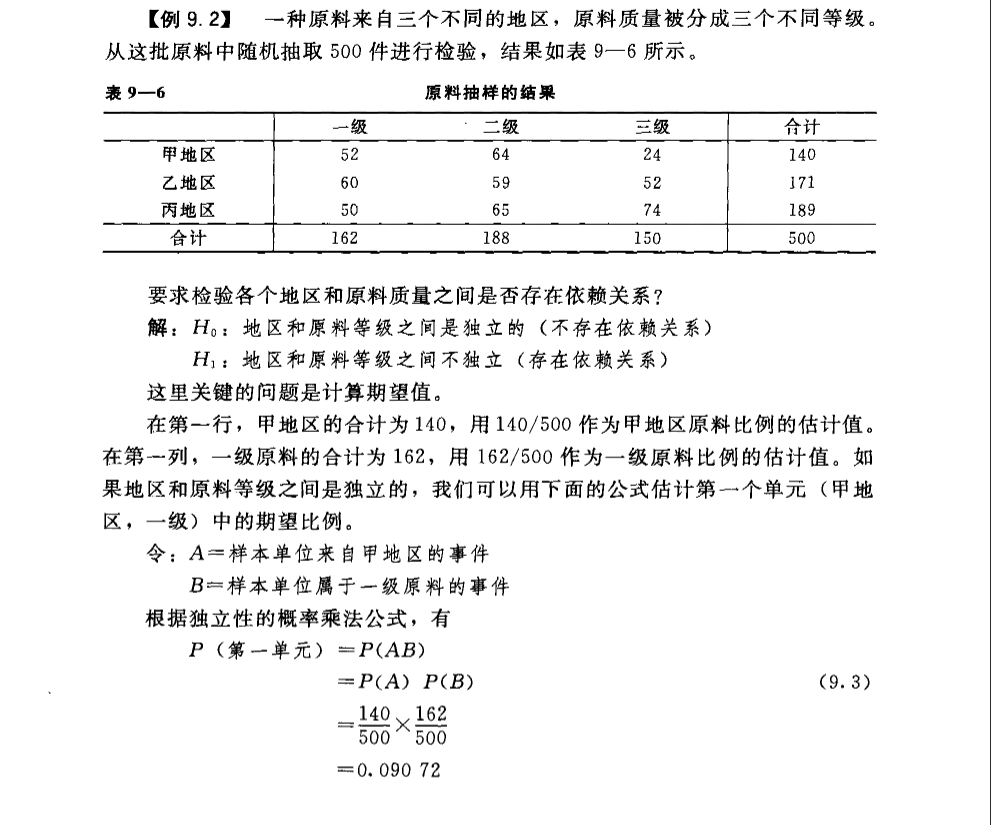
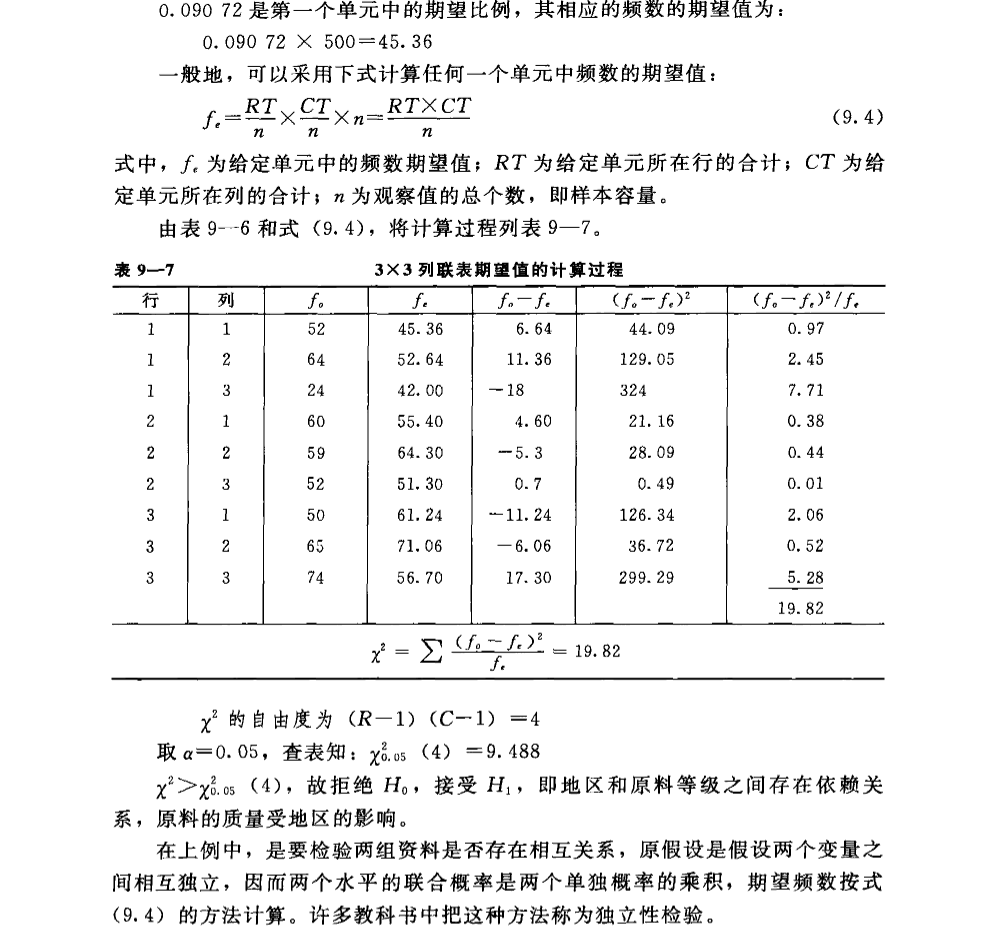
方差分析
方差分析通过检验各总体均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
方差分析的主要思想是误差分解,总误差分解为组内误差和组间误差,直观的想法:如果分类型自变量对数值型因变量没有显著影响,那么组间均方和组内均方误差应该比较接近。
以单因子方差为例,简述相关内容。
方差分析基本假定
- 每个总体服从正态分布
- 每个总体的方差必须相同(统计软件会输出方差同质性检验,如果不一致,参看另外一个统计量即可)
- 观测值是独立的(一般由实验或者抽样满足)
这三个假定成立的前提下,分析自变量对因变量是否有影响形式上转换为检验自变量的各个水平(不同的总体)的均值是否相等。因此原假设为自变量对因变量没有显著影响,即各个总体的均值全部相等。
统计量的构造
前面提到通过对总体误差的分解得到组间误差和组内误差,两者除以对应的自由度,得到组间均方(MSA)和组内均方(MSE),构造统计量 F = M S A M S E ∼ F ( k − 1 , n − k ) F = \frac{{MSA}}{{MSE}} \sim F\left( {k - 1,n - k} \right) F=MSEMSA∼F(k−1,n−k)。
回归
列联表分析可以看做研究类别型自变量和类别型因变量的关系,方差分析则是类别型自变量和数值型因变量的关系,那么回归分析可以看做研究数值型自变量和数值型因变量的关系。
基本假定
- 误差项服从均值为0的正态分布
- 误差项之间相互独立
- 误差项的方差对所有的 x x x的值都不变
逻辑
主要思想是构造误差平方和为目标函数,通过最小二乘方法求出目标函数最小时候的各个参数。通过构造不同的惩罚项,可以变形为岭回归和lasso回归。具体不赘~
求参
- 损失函数的hesse matrix是正定矩阵,所以损失函数是凸函数
- 正定矩阵定义:实对称+ A T X A > 0 A^TXA>0 ATXA>0
- 梯度下降法or随机梯度下降
逻辑回归
logstic变换
P ( Y = 1 ∣ X ) = exp ( w x ) 1 + exp ( w x ) P ( Y = 0 ∣ X ) = 1 1 + exp ( w x ) log ( P ( Y = 1 ∣ X ) P ( Y = 0 ∣ X ) ) = w x \begin{array}{l} P\left( {Y = 1|X} \right) = \frac{{\exp \left( {wx} \right)}}{{1 + \exp \left( {wx} \right)}}\\ P\left( {Y = 0|X} \right) = \frac{1}{{1 + \exp \left( {wx} \right)}}\\ \log \left( {\frac{{P\left( {Y = 1|X} \right)}}{{P\left( {Y = 0|X} \right)}}} \right) = wx \end{array} P(Y=1∣X)=1+exp(wx)exp(wx)P(Y=0∣X)=1+exp(wx)1log(P(Y=0∣X)P(Y=1∣X))=wx
目标函数和求参
极大似然估计法求参数,目标函数如下:
∏
i
[
f
(
x
i
)
]
y
i
[
1
−
f
(
x
i
)
]
1
−
y
i
{\prod\limits_i {\left[ {f\left( {{x_i}} \right)} \right]} ^{{y_i}}}\left[ {1 - f\left( {{x_i}} \right)} \right]{}^{1 - {y_i}}
i∏[f(xi)]yi[1−f(xi)]1−yi
PCA
基本思想
研究问题涉及的众多变量之间有一定的相关性,就必然存在着起支配作用的共同因素,根据这一点,通过对原始变量相关矩阵或协方差阵内部结构关系的研究,利用原始变量的线性组合形成几个综合指标(主成分),在保留原始变量主要信息的前提条件下起到降维和简化问题的作用,使得在研究复杂问题时更容易抓住主要矛盾。
基本理论
主成分定义


主成分的条件

主成分的几何意义
以二维为例:
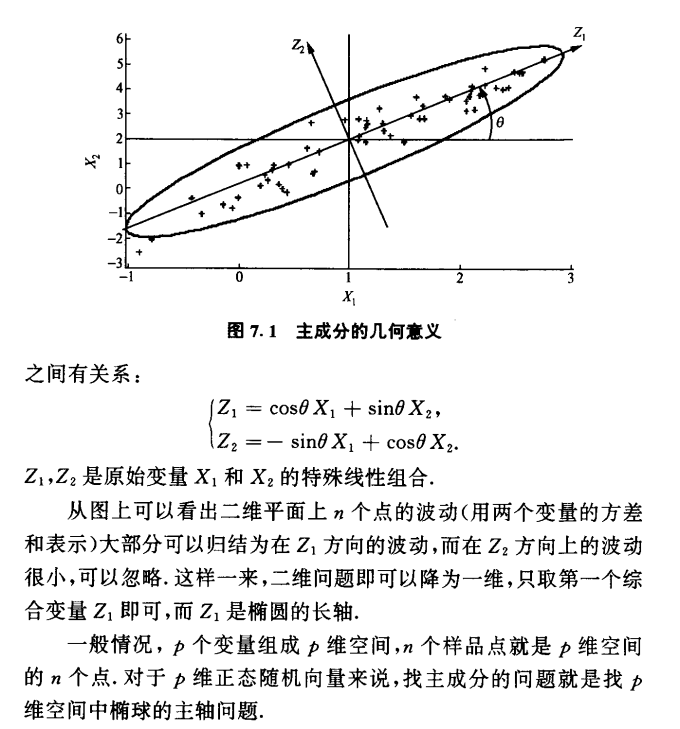
主成分的求法
目标很明确:想要
V
a
r
(
Z
1
)
Var(Z_1)
Var(Z1)最大,并且要满足前面所讲的主成分的三个条件。可以使用拉格朗日乘子法求解。具体如下:
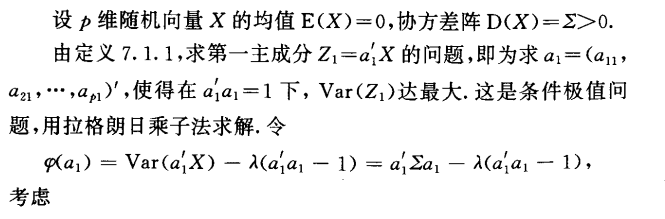

剩下的细节不多说,有空写的详细点吧。
因子分析
在主成分分析中,每一个主成分可以看做变量的线性组合;而在因子分析中,把每个变量分解成几个公共因子的线性组合和特殊因子,一般因子数量小于变量数量。
因子模型

两个假定
因子模型有两个前提假定:
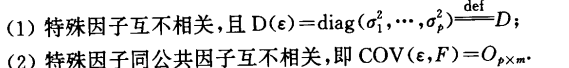
因子载荷
因子载荷矩阵为模型的汇总矩阵 A A A,矩阵中的元素 a i j a_{ij} aij表示第 i i i个变量与第 j j j个公共因子的相关系数。
参数估计
也就是载荷矩阵的求解,一般有主成分法、主因子解和极大似然法。主成分求法相当于先求出主成分,然后矩阵求逆可得。具体不太清楚,可以参看多元统计的教材。
2018-03-01 于杭州























 553
553

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








