本教程基于一个AES-256身份证号码加解密项目进行讲解,使用Python从算法底层实现每个加解密步骤,不借用Python的现有库,纯手搓,从而达到熟悉加密、解密的基本理论,懂得加密在通信中的重要作用,熟悉密码工作模式,从而设计一个加密、解密程序。
注:篇幅过长,源码请见下期
链接:
AES加密详细加密步骤实现--身份证号码加解密系统-优快云博客
一、AES加密算法介绍

AES是一种对称密钥加密算法,这意味着加密和解密使用同一把密钥。它取代了之前的老标准DES(数据加密标准),因为DES的56位密钥在现代计算能力面前已经变得不安全。
起源:1997年,美国国家标准与技术研究院(NIST)发起征集新一代加密算法的活动。最终,由两位比利时密码学家Joan Daemen和Vincent Rijmen设计的Rijndael算法在2000年胜出,并在2001年被正式确立为AES标准。
关键特性:
对称加密:加解密使用同一密钥。
分组加密:它将明文分成固定长度的块(Block) 进行加密。AES的块长度固定为128位(16字节)。
密钥长度灵活:支持128位(10轮加密)、192位(12轮加密) 和256位(14轮加密) 三种密钥长度。密钥越长,安全性越高,但计算开销也略大。128位是目前最常用的。
安全性高:至今没有已知的有效攻击方法能破解AES(除暴力穷举,但以目前的计算能力,暴力破解256位AES密钥需要宇宙年龄级别的时间)。
应用场景:由于其高效和安全,AES被广泛应用于各种领域,包括:
Wi-Fi加密(如WPA2, WPA3)
TLS/SSL(保护HTTPS网站流量)
文件加密(如WinRAR, 7-Zip)
软件和操作系统加密
安全通信应用(如Signal, WhatsApp)
二、AES加密步骤详解
AES加密过程是在一个4x4的字节矩阵(称为“状态(State)”)上进行的,这个状态初始就是16字节的明文块。整个过程包含N轮(取决于密钥长度),每一轮都对状态进行一系列可逆的变换。
一轮完整的加密(除最后一轮外)包含以下四个步骤:
1. 轮密钥加(AddRoundKey)
操作:将当前的状态矩阵与一个本轮独有的子密钥(Round Key) 进行异或(XOR)操作。
理解:这是每一步加密中直接与密钥交互的一步。子密钥是由初始的主密钥通过一个叫做“密钥扩展”(Key Expansion)的算法派生出来的。
2. 字节代替(SubBytes)
操作:通过一个非线性的替换函数(S-Box),将状态矩阵中的每一个字节替换成另一个字节。
理解:这是AES提供混淆(Confusion) 的关键步骤。S-Box的设计非常精巧,它能够抵抗各种密码学攻击(如线性密码分析和差分密码分析),确保了算法的非线性特性。
3. 行移位(ShiftRows)
操作:对状态矩阵的每一行进行循环左移。
第一行不动。
第二行向左移动1个字节。
第三行向左移动2个字节。
第四行向左移动3个字节。
理解:这一步提供了扩散(Diffusion)。它使得单个字节的变化能够在多列中传播开来,从而在多轮之后影响整个状态,消除了明文中字节的静态关系。
4. 列混合(MixColumns)
操作:对状态矩阵的每一列进行一个线性变换,将每一列视为一个多项式并与一个固定的多项式在伽罗瓦域(GF(2⁸))上进行模乘运算。
理解:这是提供扩散的另一个关键步骤。它在列上操作,确保了一个字节的变化会影响到同一列的多个字节。
注意:在最后一轮中,会省略掉列混合(MixColumns) 这一步,只进行字节代替 -> 行移位 -> 轮密钥加,以使加密过程对称,便于解密。
三、AES解密步骤
解密过程本质上是加密过程的逆序逆操作。它使用相同的子密钥,但以相反的顺序应用,并且每一步都是加密步骤的逆运算。
一轮完整的解密(除最后一轮外)包含以下四个步骤:
1. 逆行移位(InvShiftRows)
行移位的逆操作。对每一行进行循环右移。
2. 逆字节代替(InvSubBytes)
字节代替的逆操作。使用逆S-Box查表,将字节替换回原来的值。
3. 轮密钥加(AddRoundKey)
注意:这一步和解密是一样的(因为异或操作的逆操作仍然是异或)。但使用的子密钥顺序是倒序的(即从最后一个子密钥开始)。
4. 逆列混合(InvMixColumns)
列混合的逆操作。使用一个逆变换多项式来恢复原来的列。
同样,最后一轮解密也会省略逆列混合(InvMixColumns)步骤。
四、密钥扩展(Key Expansion)
如前所述,每一轮都需要一个唯一的子密钥。密钥扩展算法就是从一个初始的主密钥生成多个子密钥(也称为轮密钥)的过程。
过程:它是一个递归的过程,将初始密钥填充到一个密钥调度表中。
核心操作:包括字循环(RotWord)、字节代替(SubWord)、轮常量异或(Rcon) 等步骤,以确保每个子密钥都是不同的且与上一轮没有明显关联。
从下面开始就是基于项目的AES原理了
五、AES加密算法描述,以及对于这种算法的理解
选用算法:采用AES(Advanced Encryption Standard)对称加密算法,工作模式为CBC(Cipher Block Chaining),填充方案为PKCS7。
算法特性:
- 对称加密算法,加密解密使用相同密钥,速度快,适合处理文本等小数据。
- 支持128/192/256位密钥长度(本设计选用AES-256进行加密,安全性极高)。
- 本设计选择CBC(Cipher Block Chaining)模式,每个明文块先与前一个密文块异或后再加密,需随机初始化向量(IV)防止相同明文生成相同密文,提升安全性。
- 使用PKCS7自动补齐数据块到128位边界,填充规则明确便于解密时去除冗余,确保明文长度符合AES的16字节块大小要求。
六、设计的加密、解密程序的算法思路的描述
1、初始密钥生成和密钥扩展逻辑
1、首先用Python的key = os.urandom(32)生成一个32字节的随机密钥,也就是256位的随机初始密钥,假如生成的32字节密钥为:01 02 03 04 05 06 07 08 09 0A 0B 0C 0D 0E 0F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20
然后排列后得到如下的4行8列(256位的情况下),则其nk值就为8,列数从第0列开始
| 01 | 05 | 09 | 0D | 11 | 15 | 19 | 1D |
| 02 | 06 | 0A | 0E | 12 | 16 | 1A | 1E |
| 03 | 07 | 0B | 0F | 13 | 17 | 1B | 1F |
| 04 | 08 | 0C | 10 | 14 | 18 | 1C | 20 |
2、密钥扩展(扩展后总为240÷4=60列)
本程序采用256位密钥加密,所以我们要将初始的32字节的密钥扩展为15*16=240字节的密钥,256位加密在加密时要循环14轮,加上循环前的一轮总为15次轮密钥加操作,每个块为16个字节,所以需要240字节的密钥,需要通过计算算出其余的密钥。
分三种情况:
情况1:所要算的当前列÷nk值余数为0,注意这里的当前列要从第0列开始数到所要计算的当前列
情况2:当前列÷nk值余数不为0但是当前列÷4余数为0,这种情况只会出现在256位密钥加密的情况下
情况3:除了上面两种情况所剩下的情况
情况1:用当前列-1后对应的列进行列位移,然后用列位移(程序中排列为横向,所以为循环左移1字节)后的结果进行字节代换(S盒替换,需查S盒),再将字节代换后的结果与轮常量异或,所得到的结果再与当前列-nk值对应的列进行异或后结果就为当前列所求密钥。
示例如下:
当前的初始密钥只到第7列,而我们要求的第8列刚好满足情况1,当前列-1就为第7列,第7列为:
| 1D |
| 1E |
| 1F |
| 20 |
进行列位移后得到:
| 1E |
| 1F |
| 20 |
| 1D |
加密字节代换表(S盒)如下:
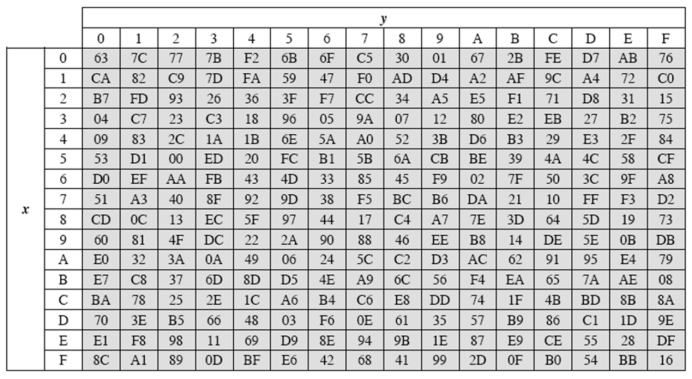
字节代换后得到(如1E查表对应的第1行第E列为72)
| 72 |
| C0 |
| B7 |
| A4 |
轮常量表为:01,02,04,08,10,20,40,80,1B,36
轮常量异或后得(只异或第1个,第一次出现情况1所以与轮常量表第一个进行异或,第二次出现就与第二个异或,以此类推)
| 73 |
| C0 |
| B7 |
| A4 |
再与当前列-nk值对应的列进行异或,第8列-nk值为0,第0列为
| 01 |
| 02 |
| 03 |
| 04 |
与第0列异或后得到第8列的密钥(对应位置进行异或,如73对应01,C0对应02)
| 72 |
| C2 |
| B4 |
| A0 |
情况2:用当前列-1对应的列进行字节代换,再用得到的结果与所求的当前列-nk值对应的列进行异或后结果就为当前列所求密钥。
在256位中第一次出现情况2的为第12列,所有计算的情况在情况1中都有涉及,按照给出的方法计算即可。
情况3:当前列-nk值对应的列与当前列-1对应的列进行异或后结果就为当前列所求密钥。
情况3的例如有第9列第10列等,对应情况3的方法计算即可。
按照上面的方法进行计算后最终可得到完整的15个轮密钥,每个轮密钥为4行4列,纵向读取组合后就得到了某轮的轮密钥,其中主轮次为14轮,还有1次初始轮密钥加。
经过计算得完整轮密钥为:
轮 0: 0102030405060708090a0b0c0d0e0f10
轮 1: 1112131415161718191a1b1c1d1e1f20
轮 2: 72c2b4a077c4b3a87eceb8a473c0b7b4
轮 3: 9e1a5d798b0c4a619216517d8f084e5d
轮 4: 40edf8b937294b1149e7f3b53a274401
轮 5: 1ed6460595da0c6407cc5d1988c41344
轮 6: 6a90e3ae5db9a8bf145e5b0a2e791f0b
轮 7: 2f6a862ebab08a4abd7cd75335b8c417
轮 8: cbbe13389607bb878259e08dac20ff86
轮 9: 4ddd3db9f76db7f34a1160a07fa9a4b7
轮 10: 19b45dcb8fb3e64c0dea06c1a1caf947
轮 11: ad007c195a6dcbea107cab4a6fd50ffd
轮 12: 71c2ed63fe710b2ff39b0dee5251f4a9
轮 13: add171dbf7bcba31e7c0117b88151e86
轮 14: 68b07a7496c1715b655a7cb5370b881c
3、加密流程
输入验证:校验18位身份证号格式(前17位数字,末位为数字/X,X不区分大小写),假如输入的身份证号为:123456200001011234(由于最后一位可能是X,所以为ASCII编码的18字节字符)
将身份证号码转为16进制的ASCII编码为:31 32 33 34 35 36 32 30 30 30 30 31 30 31 31 32 33 34
由于身份证号码只有18字节,所以用PKCS7填充方案将其填充至32位,也就是16的整数倍,32-18=14,所以按照PKCS7的规则要填充14个16进制的14即14个0E
填充后明文如下:
31 32 33 34 35 36 32 30 30 30 30 31 30 31 31 32 | 前16字节 ("1234562000010112")
33 34 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E | 后16字节 ("33 34" + 14个0x0E)
初始化向量(IV)的生成:
本程序采用CBC工作模式,所以需要初始化向量,由Python中的iv = os.urandom(16) 生成16字节随机初始向量,需要加密的每个块为16字节,所以生成16字节的IV,用于与第一块明文进行异或,假如IV为:00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00(示例用全0,实际随机生成)
密钥的生成:
假如以0102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E1F20为初始的密钥,根据上面的规则进行密钥扩展可得到全部的轮密钥
指纹的生成:
通过对原始密钥key 进行 SHA-256 哈希运算,生成 32字节的哈希值,截取哈希值的前 4字节作为密钥指纹。直接使用Python中哈希库的API进行计算:hashlib.sha256(key).digest()[:4],这样指纹与密钥强关联,但无法通过指纹反推密钥(哈希的不可逆性),即使密钥仅有一位不同,哈希结果也会完全不同(雪崩效应),从而防止通过指纹猜测密钥内容。使用密钥得到指纹,SHA256哈希前4字节为 ae216c2e
接下来就是分块处理:
块1(16字节) : 31 32 33 34 35 36 32 30 30 30 30 31 30 31 31 32
块2(16字节) : 33 34 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E 0E
以处理第一块明文为例:
第一块明文为:31 32 33 34 35 36 32 30 30 30 30 31 30 31 31 32
状态矩阵初始化(按列填充):
| 31 | 35 | 30 | 30 |
| 32 | 36 | 30 | 31 |
| 33 | 32 | 30 | 31 |
| 34 | 30 | 31 | 32 |
与初始化向量(IV)进行异或:
由于IV全为0,所以明文块不变,对应位置的进行异或
| 31 | 35 | 30 | 30 |
| 32 | 36 | 30 | 31 |
| 33 | 32 | 30 | 31 |
| 34 | 30 | 31 | 32 |
| 00 | 00 | 00 | 00 |
| 00 | 00 | 00 | 00 |
| 00 | 00 | 00 | 00 |
| 00 | 00 | 00 | 00 |
得到新的状态矩阵:
| 31 | 35 | 30 | 30 |
| 32 | 36 | 30 | 31 |
| 33 | 32 | 30 | 31 |
| 34 | 30 | 31 | 32 |
初始轮密钥加(第0轮),没进入循环前:
选择轮密钥中的哪16个字节进行轮密钥加呢:从当前轮数*4的列向后取4列
初始轮密钥加使用的轮密钥如下:
| 01 | 05 | 09 | 0D |
| 02 | 06 | 0A | 0E |
| 03 | 07 | 0B | 0F |
| 04 | 08 | 0C | 10 |
与上一步的到的状态矩阵进行异或得到新的状态矩阵:
对应位置进行异或,如依次为31对应01,32对应02
| 30 | 30 | 39 | 3D |
| 30 | 30 | 3A | 3F |
| 30 | 35 | 3B | 3E |
| 30 | 38 | 3D | 22 |
进入主轮次循环,总共14轮,这里以第1轮为例:
加密过程循环中的步骤为:
S盒替换(字节替换)-> 行位移 -> 列混淆(最后一轮不进行)-> 轮密钥加
S盒替换(字节替换):
用初始轮密钥加得到的状态矩阵进行字节替换(查S盒)得到新状态矩阵:
| 04 | 04 | 12 | 27 |
| 04 | 04 | 80 | 75 |
| 04 | 96 | E2 | 75 |
| 04 | 07 | 27 | 93 |
行位移:
第一行不变
第二行左循环移动1个字节
第三行左循环移动2个字节
第四行左循环移动3个字节
得到新状态矩阵:
| 04 | 04 | 12 | 27 |
| 04 | 80 | 75 | 04 |
| E2 | 75 | 04 | 96 |
| 93 | 04 | 07 | 27 |
列混淆:
使用GF(2^8)对[列混淆左乘矩阵的行]与[当前字节的列] 进行矩阵乘法(伽罗瓦域运算)
加密列混淆左乘矩阵如下:
[0x02, 0x03, 0x01, 0x01]
[0x01, 0x02, 0x03, 0x01]
[0x01, 0x01, 0x02, 0x03]
[0x03, 0x01, 0x01, 0x02]
假如我们算状态矩阵中第三行第一列的E2列混淆后的值,所以我们要用到状态矩阵的第一列,
| 04 |
| 04 |
| E2 |
| 93 |
由于是第三行,所以左乘矩阵中我们也要选第三行即[0x01, 0x01, 0x02, 0x03],通过公式得到如下式子:
01*04+01*04+02*E2+03*93,其中的加法在最后全部换成异或运算即可。
我们假设状态矩阵中的值都为a,则有01*a+01*a+02*a+03*a,即:
01*a
01*a
02*a
03*a
1、首先我们定义一个函数f(a)
如果a小于0x80(十进制128),则返回2*a,如果a大于等于0x80则返回((2*a)mod0x100)XOR 0x1B
2、当乘法操作中有一个值为2的n次方时可用如下公式:
0x01*a=a
0x02*a=f(a)
0x04*a=f(0x02*a)=f(f(a))
0x08*a=f(0x04*a)=f(f(f(a)))
以此类推,注意这里所说的2^n所等于的值为十进制的值,而例如0x04这些是十六进制的,0x04对应的十进制为4,0x10应的为16
3、当乘法操作中不满足2的n次方的情况,如03*a,则:
03*a=02*a+01*a=02*a⊕01*a,而02*a又满足有值为2的n次方的情况,所以用其方法进行计算
分解:
01*04=04
01*04=04
02*E2这里需要判断如果0xE2不小于0x80,则需要进行如下计算:
由于E2大于80,所以返回((2*0xE2)mod0x100)XOR 0x1B
计算得DF,如果小于80则返回2*E2即可
03*93=02*93+01*93
其中02*93中93大于80,所以((2*0x93)mod0x100)XOR 0x1B
得3D,加法换成异或运算,即3D XOR 93=AE
最后E2列混淆后为01*04+01*04+02*E2+03*93=04⊕04⊕DF⊕AE=71
其余的也用上面这种方法进行计算即可,最终算完得到新状态矩阵为:
| 75 | E2 | B8 | F3 |
| A2 | 84 | F3 | A9 |
| 71 | 62 | 66 | 7D |
| D7 | F1 | 49 | B5 |
轮密钥加,对应位置异或:
这次所用密钥为:
| 11 | 15 | 19 | 1D |
| 12 | 16 | 1A | 1E |
| 13 | 17 | 1B | 1F |
| 14 | 18 | 1C | 20 |
得到新状态矩阵:
| 64 | F7 | A1 | EE |
| B0 | 92 | E9 | B7 |
| 62 | 75 | 7D | 62 |
| C3 | E9 | 55 | 95 |
最后将得到的这个新状态矩阵带入第二轮循环,第二轮最后得到的状态矩阵带入第三轮,以此类推完成14轮,但是最后一轮不需要进行列混淆操作,直接用行位移得到的状态矩阵进行轮密钥加即可得到第一块最后的矩阵即密文,在CBC模式下,在进行第二块明文加密前,需要将第二块明文的初始状态矩阵与第一块密文矩阵进行对应位置的异或后再进行与IV异或、初始轮密钥加、主轮次循环等操作,将所有密文组合就得到密文,最后组合IV+指纹+密文通过base64编码后就得到最终密文,未进行base64 编码前其中IV占16字节+指纹4字节+密文块1的16字节+密文块2的16字节
输出保存:追加写入密文文件
4、解密流程
输入选择:文件加载或手动输入Base64密文,然后用base64解码成组合状态的密文
密文分组:
Base64解密后为IV占16字节+指纹4字节+密文块1的16字节+密文块2的16字节,我们将前面的20个字节拆除,剩余的就是32字节的密文,然后对密文进行分组即可。
这里我们以刚才加密的密文块1为例进行解密,对解密来说即初始状态矩阵:
| 64 | F7 | A1 | EE |
| B0 | 92 | E9 | B7 |
| 62 | 75 | 7D | 62 |
| C3 | E9 | 55 | 95 |
进入主轮次解密循环,总14轮,以第14轮为例,加密时为第一轮,解密时就为第14轮:
使用的轮密钥与加密时使用的一致,但是解密时需要将轮密钥逆向使用,轮密钥14(最后一个轮密钥)→ 轮密钥0(初始密钥)
解密过程循环中的步骤为:
轮密钥加 -> 逆列混淆(第一轮不进行)-> 行位移 -> S盒替换(字节替换)
选择轮密钥中的哪16个字节进行轮密钥加呢:(60-当前轮数*4)的列向后取4列
轮密钥加:
使用的密钥为:
| 11 | 15 | 19 | 1D |
| 12 | 16 | 1A | 1E |
| 13 | 17 | 1B | 1F |
| 14 | 18 | 1C | 20 |
与状态矩阵对应位置字节进行异或的新状态矩阵:
| 75 | E2 | B8 | F3 |
| A2 | 84 | F3 | A9 |
| 71 | 62 | 66 | 7D |
| D7 | F1 | 49 | B5 |
逆列混淆:
使用GF(2^8)对[列混淆左乘矩阵的行]与[当前字节的列] 进行矩阵乘法(伽罗瓦域运算)
解密列混淆左乘矩阵如下:
[0x0E, 0x0B, 0x0D, 0x09]
[0x09, 0x0E, 0x0B, 0x0D]
[0x0D, 0x09, 0x0E, 0x0B]
[0x0B, 0x0D, 0x09, 0x0E]
这次以求状态矩阵第4行第1列的逆列混淆后的值为例,根据公式要用到状态矩阵的第一列:
| 75 |
| A2 |
| 71 |
| D7 |
要用到左乘矩阵的第4行即[0x0B, 0x0D, 0x09, 0x0E],得到如下公式:
0B*75+0D*A2+09*71+0E*D7,加法换成异或运算即可。
分解:
0B*75
这里0B不属于2的n次方且75小于0x80,可写为:
0B*75=08*75+03*75=f(04*75)+02*75+01*75=f(f(02*75))+02*75+01*75=
f(f(f(75)))+02*75+01*75
这里75小于0x80,所以得2*75=EA,
得f(f(EA)),EA大于0x80,得((2*EA)mod 0x100)XOR 0x1B=CF,
得f(CF),CF大于0x80,得((2*CF)mod 0x100)XOR 0x1B=85,
最后得0B*75=85+02*75+01*75=85⊕EA⊕75=1A,
同理可得
0D*A2=08*A2+04*A2+1*A2=f(f(f(A2)))+f(f(A2))+A2=67+BE+A2=7B
09*71=08*71+01*71=f(f(f(71)))+71=A5+71=D4
0E*D7=08*D7+04*D7+02*D7=f(f(f(D7)))+f(f(D7))+f(D7)=E2+71+B5=26
最终的第4行第1列的逆列混淆后的值为1A⊕7B⊕D4⊕26=93
按照上面的方法计算其他的值最终得到新状态矩阵:
| 04 | 04 | 12 | 27 |
| 04 | 80 | 75 | 04 |
| E2 | 75 | 04 | 96 |
| 93 | 04 | 07 | 27 |
逆行位移
加密时是循环左移,那么解密时就变为循环右移:
第一行不变
第二行右循环移动1个字节
第三行右循环移动2个字节
第四行右循环移动3个字节
得到新状态矩阵:
| 04 | 04 | 12 | 27 |
| 04 | 04 | 80 | 75 |
| 04 | 96 | E2 | 75 |
| 04 | 07 | 27 | 93 |
S盒替换(字节替换):
解密字节代换表(逆S盒)如下:
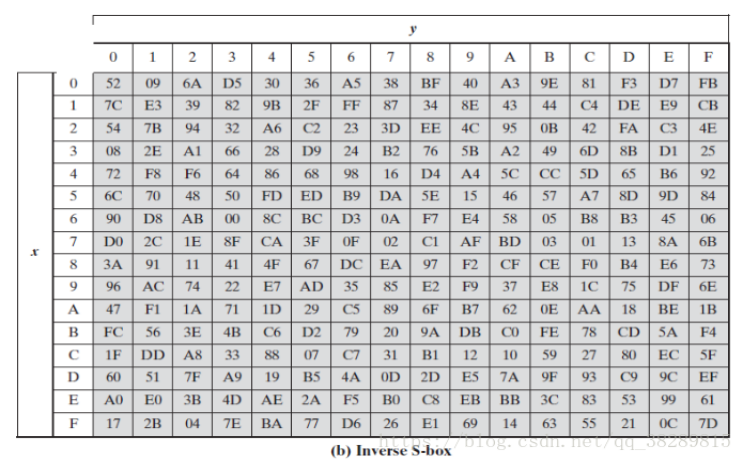
根据加密是相同的方法进行替换后得到新状态矩阵:
| 30 | 30 | 39 | 3D |
| 30 | 30 | 3A | 3F |
| 30 | 35 | 3B | 3E |
| 30 | 38 | 3D | 22 |
因为上面的演示相当于密文块1解密的最后一轮循环,所以循环完后得到的矩阵是加密时第0轮密钥加得到的矩阵,所以还要与初始密钥进行一轮轮密钥加操作:
初始密钥为:
| 01 | 05 | 09 | 0D |
| 02 | 06 | 0A | 0E |
| 03 | 07 | 0B | 0F |
| 04 | 08 | 0C | 10 |
轮密钥加后得到加密时与初始化向量(IV)异或后的矩阵:
| 31 | 35 | 30 | 30 |
| 32 | 36 | 30 | 31 |
| 33 | 32 | 30 | 31 |
| 34 | 30 | 31 | 32 |
再与IV(加密时为全0)进行异或后得到十六进制的ASCII编码的明文:
| 31 | 35 | 30 | 30 |
| 32 | 36 | 30 | 31 |
| 33 | 32 | 30 | 31 |
| 34 | 30 | 31 | 32 |
即31323334353632303030303130313132--->1234562000010112
第一块密文解密完成,但是需要注意,如果是第二块密文解密到当前这一步后,还要与第一块的密文进行异或才能得到明文,最后将两块解密好的明文组合在一起,读取最后一个字节的值,也就是0x0E,其十进制为14,去除明文中最后的14个字节即可得到加密前的身份证号了。
结果展示:明文身份证号或错误提示
七、设计的加密、解密程序的流程图
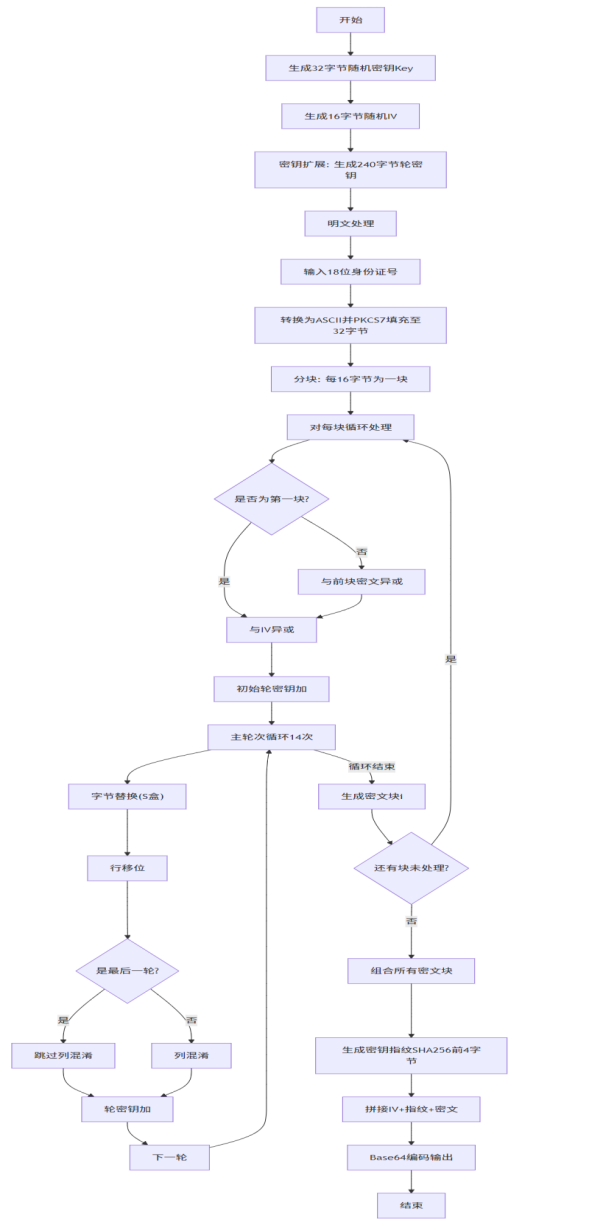
加密流程图:
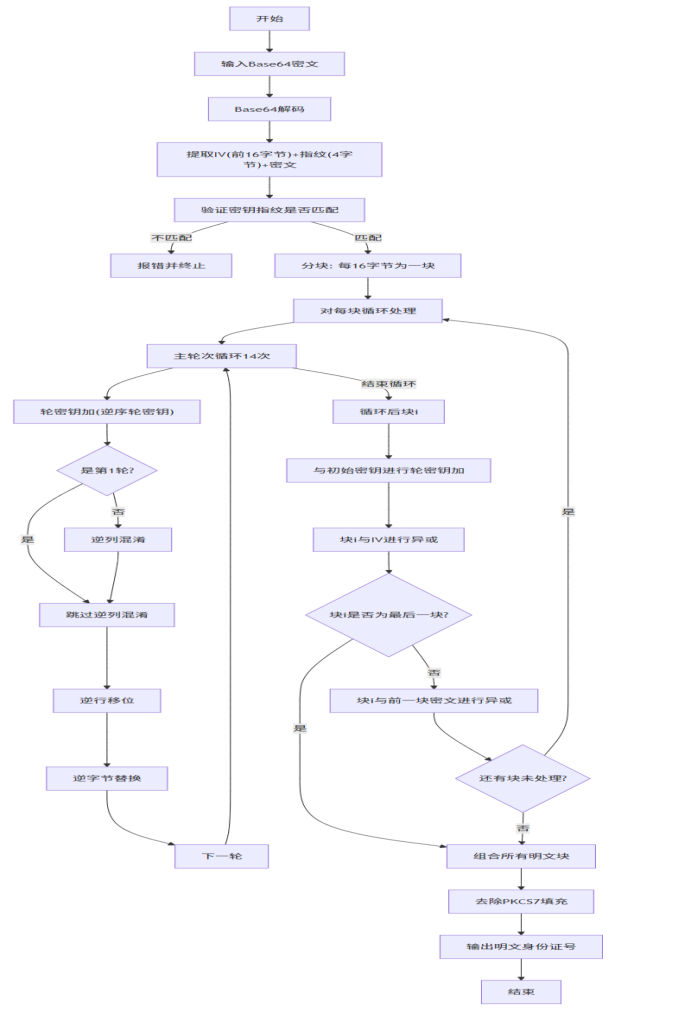
解密流程图:
八、总结
| 特性 | 描述 |
| 算法类型 | 对称分组密码 |
| 分组长度 | 128位(16字节) |
| 密钥长度 | 128, 192, 256位 |
| 加密轮数 | 10(128位),12(192位),14(256位) |
| 核心步骤 | AddRoundKey, SubBytes, ShiftRows, MixColumns |
| 设计原则 | 混淆(SubBytes)和扩散(ShiftRows, MixColumns) |
| 安全性 | 极高,是目前的全球加密标准 |
简单来说,AES加密就像是对数据块进行一场复杂而精致的“洗牌”和“替换”游戏,每一轮都使用不同的密钥片段,经过多轮操作后,原始明文就变成了完全随机、无法识别的密文。而其逆向过程(解密)则能准确地将其恢复原状。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










