L型骨牌覆盖特殊棋盘问题解析-优快云博客

本文探讨了棋盘覆盖问题，特别是在一个2k×2k的特殊棋盘中，如何使用四种不同形态的L型骨牌覆盖所有方格，但不包括一个特殊方格。通过递归方法和棋盘分割策略，对C++和Java编程语言的实现进行了说明。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

棋盘覆盖问题

在一个2^k✖2^k个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为特殊方格，并且这个棋盘就称为特殊棋盘。显然，这个特殊方格在棋盘中出现的位置由4^k中情形；例如当 k = 2 时，特殊方格可以是16个方格中的任意一格；
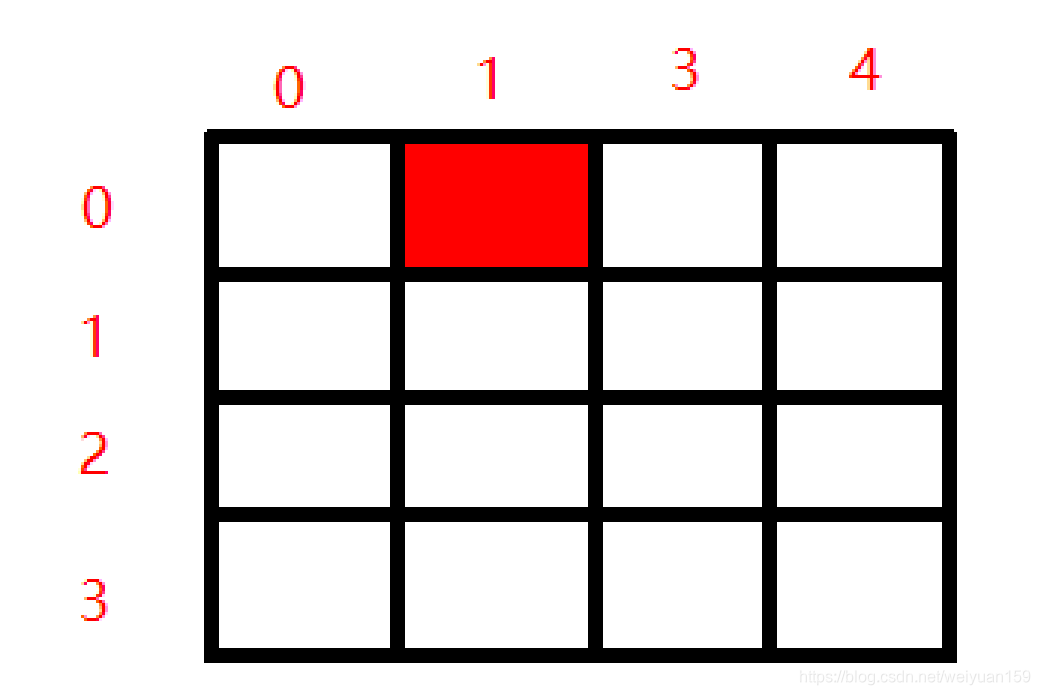
在这里插入图片描述

如上图（1）所示，数组【0】【1】的位置就是特殊方格的位置，这个特殊方格可以在16个方格中的任意位置。
然后，要用如下图（2）四种不同形态的L型骨牌覆盖掉除特殊方格中的所有方格，条件是不得重叠，即一个格子中不得覆盖两次及以上的L型骨牌。
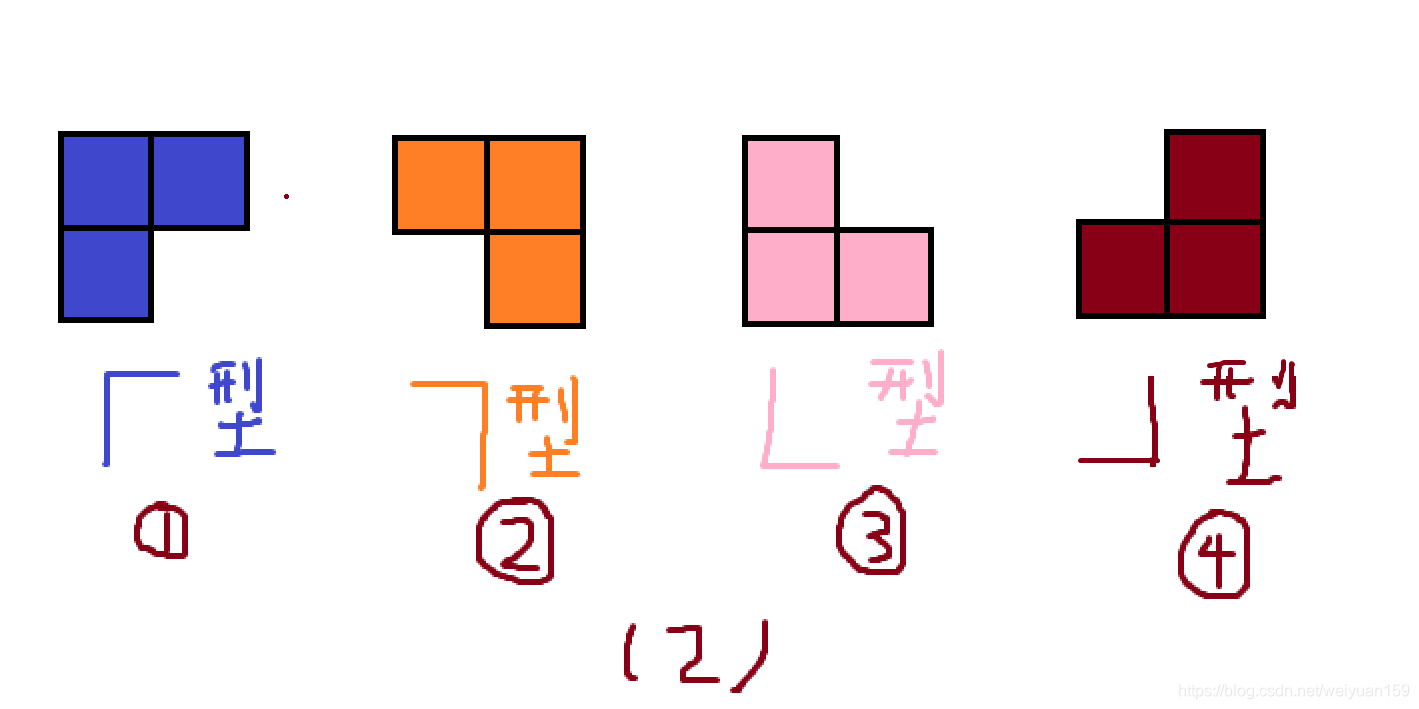
在这里插入图片描述
将上图中所示的四种型号的骨牌对图一进行覆盖填充，除特殊棋盘为刚好能覆盖掉整个棋盘，结果如下所示。

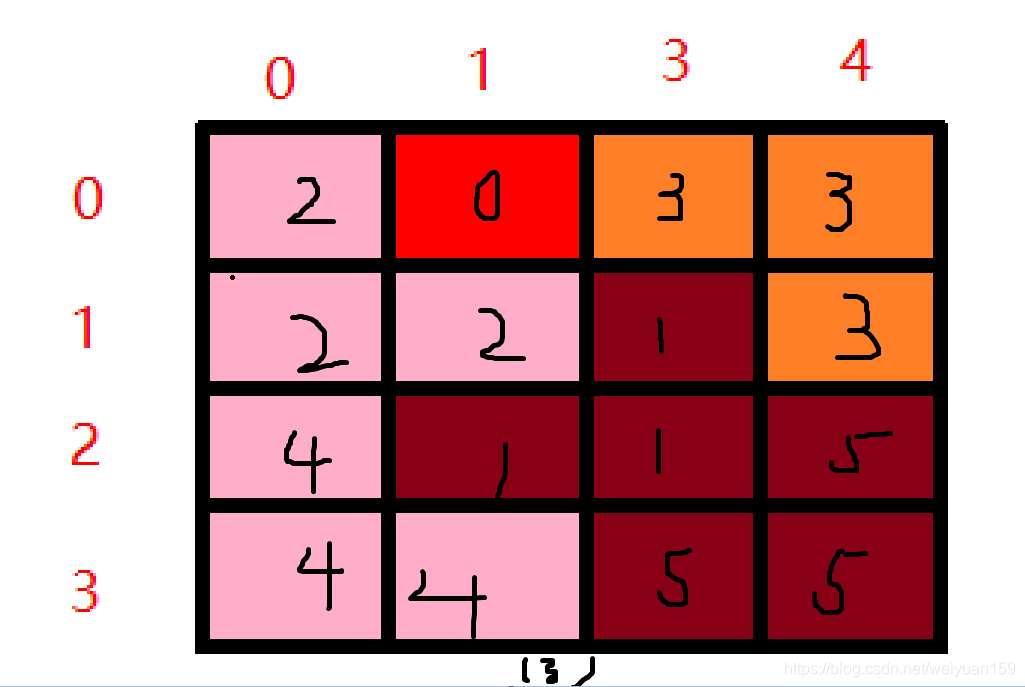
在这里插入图片描述
下面进行棋盘的覆盖（途中特殊方格表示0，数字下标位置为【0】【1】），所用到的方法是：

先将图中所示棋盘分割为4小格，即将size为4×4的格子分成4个2×2的格子（当k>0时，将2^k×2^k棋盘分割为4个2^k-1×2^k-1子棋盘）。
我们分别叫它左上、右上、左下、右下棋盘，如果特殊棋盘在左上（子棋盘中），我们将没有特殊方格所在的其他三个子棋盘进行覆盖，如上图标1的地方，（当然这不是第一步就把1标注在图所在位置上，因为棋盘覆盖使用了递归的方法，这里只是为了便于理解）。
继续进行棋盘分割，直至棋盘分割到最小单元（1×1的子棋盘）

用编程语言进行实现，主要时利用了二维数组，首先定义棋盘的大小，之后输入特殊方格所在的位置（数组下标），然后在二维数组中进行相同数字(一组相同数组表示4种L型骨牌中的一个)的填充（即覆盖）

c++代码的实现


#include <iostream>
#include <cstring>
#include <cstdio>
 
using namespace std;
//tr表示棋盘左上角行号
//tc表示棋盘左上角列号
//dr表示特殊棋盘的行号
//dc表示特殊棋盘的列号
//size = 2^k
//棋盘的规格为2^k * 2^k
const int SIZE = 8;
static int tt = 1;
static int board[SIZE][SIZE];
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
   
   
    if(size == 1)//棋盘只有一个方格且是特殊方格
        return ;
    int t = tt++; //L型骨牌号
    int s = size>>1;//分割棋盘
     //覆盖左上角子棋盘
    if(dr<tr+s&&dc<tc+s)
        ChessBoard(tr,tc,dr,dc,s); //特殊方格在此棋盘中
    else
    {
   
   
         //此棋盘无特殊方格
         //用t号L型骨牌覆盖右下角
        board[tr+s-1][tc+s-1] = t;
        //覆盖其余方格
        ChessBoard(tr,tc,tr+s-1,tc+s-1,