一文带你掌握动态规划（三）

在前面两节中，我们分别学习了动态规划的原理，解题步骤，以及讲解了5种类型的经典动态规划题，分别是简单dp问题，路径问题，多状态dp，子数组问题以及子序列问题，建议没看过前面内容的先看一下前面的章节。

一文带你掌握动态规划（一）：一文带你掌握动态规划（一）-优快云博客

一文带你掌握动态规划（二）：一文带你掌握动态规划（二）-优快云博客

---

---

这一篇文章，将会讲解动态规划剩下的内容，有回文串问题，两个数组的dp问题，还有非常经典的01背包问题，废话不多说，直接开始今天的学习吧！

1. 回文串问题

回文串指的是正着读反着读都是一样的字符串，比如abcba,aabbcc。

在回文串问题中，动态规划的思想可能不是最优解，但是通过动态规划可以大大降低题目的难度，比如我们可以将所有子串是否是回文串的信息保存起来，空间复杂度O(N^2)，有了这个信息后，很多题目都迎刃而解了

1.1 回文子串

题目连接：647. 回文子串 - 力扣（LeetCode）

​

子串和子数组是一样的，选出的结果是一个连续的区间。

算法原理：

状态表示

根据经验（这里的经验通常指的是以一个位置为结尾怎么怎么样 / 以一个位置为开头怎么怎么样）+ 题目要求，我们将dp[i][j]表示为：s字符串[i, j]区间的字符串是否为回文串。

状态转移方程

状态转移方程也很好得到，只需要判断s字符串的[i, j]区间是否是回文串即可。

先判断i位置和j位置，如果s[i] != s[j]，那么就说明这段区间无法构成回文串，如果s[i] == s[j]，那么就继续判断s[i+1]和s[j-1]，也就是dp[i+1][j-1]。

​

总结

1.状态表示：dp[i][j]表示为：s字符串[i, j]区间的字符串是否为回文串。
2.推导状态转移方程：

​

3.初始化：将dp表初始化为false，默认不存在回文串
4.填表：dp[i+1][j-1]位于dp[i][j]的左下角，也就是说在填dp[i][j]时，至少要填好dp[i+1][j-1]，所以我们从下往上填表
5.返回值：返回所有dp[i][j]中true的个数。

题解：

class Solution 
{
public:
    int countSubstrings(string s) 
    {
        int n = s.size();
        //dp[i][j]表示为：s字符串[i, j]区间的字符串是否为回文串。
        vector<vector<bool>> dp(n, vector<bool>(n, false));

        int ret = 0;
        for (int i = n - 1; i >= 0; --i)
        {
            for (int j = i; j < n; ++j)
            {
                //判断s[i, j]能否构成回文串
                if (s[i] != s[j])
                    dp[i][j] = false;
                else 
                {
                    if (i == j)
                        dp[i][j] = true;
                    else if (i + 1 == j)
                        dp[i][j] = true;
                    else 
                        dp[i][j] = dp[i+1][j-1];
                }

                //统计结果
                ret += dp[i][j];
            }
        }
        return ret;
    }
};

虽然最终的时间效率不高，但是前面也说了，这题的动态规划思想是非常重要的，很多回文串问题，都可以通过上面的方法，将所有字串是否是回文串的结果保存起来，有个这个结果，可以将困难题变成简单题。

1.2 最长回文子串

题目链接：5. 最长回文子串 - 力扣（LeetCode）

​

算法原理：

状态表示

根据经验 + 状态表示，我们可以将dp[i][j]表示为：s字符串[i, j]区间内的子串能否构成回文串

状态转移方程

状态转移方程也很好得到，只需要判断s字符串的[i, j]区间是否是回文串即可。

先判断i位置和j位置，如果s[i] != s[j]，那么就说明这段区间无法构成回文串，如果s[i] == s[j]，那么就继续判断s[i+1]和s[j-1]，也就是dp[i+1][j-1]。

​

在有了dp[i][j]后，我们就可以通过计算[i, j]区间的大小来得到这个回文串的长度，根据这个长度我们就能找到最长的回文子串。

总结

1.状态表示：dp[i][j]表示为：s字符串[i, j]区间的字符串是否为回文串。
2.推导状态转移方程：

​

3.初始化：将dp表初始化为false，默认不存在回文串
4.填表：dp[i+1][j-1]位于dp[i][j]的左下角，也就是说在填dp[i][j]时，至少要填好dp[i+1][j-1]，所以我们从下往上填表
5.返回值：返回表中dp[i][j] == true并且 j - i + 1值最大的s字符串的子串。

题解：

class Solution 
{
public:
    string longestPalindrome(string s) 
    {
        //dp[i][j]表示为：s字符串[i, j]区间内的子串能否构成回文串
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n, false));

        string ret;
        for (int i = n - 1; i >= 0; --i)
        {
            for (int j = i; j < n; ++j)
            {
                if (s[i] == s[j])
                {
                    if (i == j || i + 1 == j)
                        dp[i][j] = true;
                    else
                        dp[i][j] = dp[i+1][j-1];
                }
                //如果ret的大小比[i,j]区间小，则更新ret
                if (dp[i][j] == true && ret.size() < j - i + 1)
                    ret = s.substr(i, j - i + 1);
            }
        }

        return ret;
    }
};

1.3 分割回文串IV

题目链接：1745. 分割回文串 IV - 力扣（LeetCode）

​

这题的暴力解法是：固定一个i位置和一个j位置，那么就可以将整个s字符串分割成三份，第一份是[0, i-1]，第二份是[i, j-1]，第三份是[j, n-1]，然后判断这三个区间是否是回文串，判断方法是选取找个区间的头和尾，然后向中间遍历，遍历时要保证s[i] == s[j]，那么判断回文串的时间复杂度就是O(N)，那能否找到一个快速判断回文串的方法？

其实第一题就已经给过我们答案了，只要按“回文子串那题的思路”，先将所有的子串判断是否是回文并将结果保存到dp表中，那么判断回文串的时间复杂度就能变成O(1)

算法原理：

状态表示

根据经验 + 状态表示，我们可以将dp[i][j]表示为：s字符串[i, j]区间内的子串能否构成回文串

状态转移方程

状态转移方程也很好得到，只需要判断s字符串的[i, j]区间是否是回文串即可。

先判断i位置和j位置，如果s[i] != s[j]，那么就说明这段区间无法构成回文串，如果s[i] == s[j]，那么就继续判断s[i+1]和s[j-1]，也就是dp[i+1][j-1]。

​

总结

1.状态表示：dp[i][j]表示为：s字符串[i, j]区间的字符串是否为回文串。
2.推导状态转移方程：

​

3.初始化：将dp表初始化为false，默认不存在回文串
4.填表：dp[i+1][j-1]位于dp[i][j]的左下角，也就是说在填dp[i][j]时，至少要填好dp[i+1][j-1]，所以我们从下往上填表
5.返回值：如果能找到一个i，j，满足dp[0][i-1] == true && dp[i][j-1] == true && dp[j][n-1] == true，那么就返回true，如果找不到就返回false。

class Solution 
{
public:
    bool checkPartitioning(string s) 
    {
        //用动态规划，将s的所有子串都判断是否是回文串并将结果保存至dp表中
        int n = s.size();
        //dp[i][j]表示：s的[i, j]区间的子串是否是回文串
        vector<vector<bool>> dp(n, vector<bool>(n, false));

        for (int i = n - 1; i >= 0; i--)
        {
            for (int j = i; j < n; j++)
            {
                if (s[i] == s[j])
                {
                    if(i == j || i + 1 == j)
                        dp[i][j] = true;
                    else 
                        dp[i][j] = dp[i + 1][j - 1];
                }
            }
        }

        //判断能否分割成三个非空回文子字符串
        //[0, i-1] [i, j-1] [j, n-1]
        for (size_t i = 1; i < n; i++)
        {
            for (size_t j = i + 1; j < n; j++)
            {
                if (dp[0][i-1] && dp[i][j-1] && dp[j][n-1])
                    return true;
            }
        }
        return false;
    }
};

这道题很好的印证了，虽然这是一道困难题，但是有了动态规划的回文串思想，那么做起来其实非常简单。

1.4 分割回文串II

题目链接：LCR 094. 分割回文串 II - 力扣（LeetCode）

​

这道题和前面（动态规划第二讲）中有一道题比较相似，就是单词拆分，这题的解题思路也和那道题差不多。

算法原理：

状态表示

根据经验和状态表示，将dp[i]表示为，区间[0, i]的字符串最少能分割多少次。

状态转移方程

我们可以将[0, i]区间的字符串分为以下两种情况

• 1. [0, i]区间的字符串是回文串，dp[i] = 0
• 2. [0, i]区间的字符串不是回文串，那么我们就要在[0, i]区间内找到一个j，使得[j, i]是回文串，那么接下来我们还要保证[0, j-1]区间是回文串，只要在[0, j-1]区间内继续寻找一个k，使得[k, j-1]为回文串，以此类推....直到[0, i]可以被分成多个回文串。而dp[j-1]正好保存的就是[0, j-1]区间最少分割次数。

​

在[0, i]区间内可能存在多个j满足，[j, i]是回文串，我们需要找到其中最小的那个，所以dp[i] = min(dp[j - 1] + 1)。 

在这个过程中，我们需要大量判断是否是回文串，而判断回文串的时间复杂度是O(N)，我们可以根据前面的经验进行优化，将所有子串是否是回文串的信息保存在dp表中,  这样判断回文串的时间复杂度就变成O(1)

总结

1. 预处理：将所有子串是否是回文的信息保存至dp表中
2. 状态表示： dp[i]表示为，区间[0, i]的字符串最少能分割多少次
3. 推导状态转移方程：​
4. 初始化：将dp表所有的值初始化为INT_MAX，保证填表时不会干扰
5. 填表：从左往右
6. 返回值：返回dp[n-1]

class Solution 
{
public:
    int minCut(string s) 
    {
        //将s的所有子串是否是回文串的信息保存起来
        int n = s.size();
        vector<vector<bool>> status(n, vector<bool>(n, false));

        for (int i = n - 1; i >= 0; i--)
        {
            for (int j = i; j < n; j++)
            {
                if (s[i] == s[j])
                {
                    if (i == j || i + 1 == j)
                        status[i][j] = true;
                    else 
                        status[i][j] = status[i+1][j-1];
                }
            }
        }

        //动态规划找到s的[0, n-1]区间的最少分割次数
        vector<int> dp(n, INT_MAX);
        for (int i = 0; i < n; i++)
        {
            //如果[0,i]区间就是一个回文串，则一次都不需要分
            if (status[0][i] == true)
            {
                dp[i] = 0;
            }
            else 
            {
                //在(0, i]区间中找到一个j，使得[j, i]是回文串
                //则dp[i]的最少分割次数就是在dp[j-1]基础上+1
                for (int j = 1; j <= i; j++)
                {
                    if (status[j][i] == true)
                        dp[i] = min(dp[i], dp[j-1] + 1);
                }
            }
        }

        return dp[n-1];
    }
};

1.5 最长回文子序列

题目链接：516. 最长回文子序列 - 力扣（LeetCode）

​

算法原理：

状态表示

根据经验+题目要求，我们可以将dp[i]表示为：以 i 位置为结尾的所有子序列中，最长的回文子序列，但是看过子序列那一节的同学，这里可能已经意识到了，一维的dp表是更新不出来的，因为dp表中保存的只是长度，那么其实我们无法找到一个 j，使得 i 跟在 j 后面还是一个回文串。

我们可以让[i, j]表示一段区间，dp[i][j]表示：[i, j]区间内的所有子序列中，最长的回文子序列的长度。 

状态转移方程

推导状态转移方程时，要根据最近的一步来推导。dp[i][j]，如果s[i] == s[j]，那么还有以下几种情况

• 1.i == j，此时dp[i][j] = 1   
• 2.i + 1 == j，此时dp[i][j] = 2  
• 3.其他，dp[i][j] = dp[i+1][j-1] + 2

如果s[i] != s[j]，那么最终的回文子序列一定不能同时以i开头，j结尾，此时我们可以去[i, j-1]区间和[i+1, j]区间内继续查找。

所以dp[i][j] = max(dp[i][j-1], dp[i+1][j])。

​

有人可能会有疑问，既然不能同时以i开头，j结尾，为什么找到是[i,j-1]区间和[i+1,j]区间，而不去[i+1,j-1]区间再找找，其实画个图就明白了，[i+1, j-1]会包含在两种情况之中，这两种情况已经将[i+1, j-1]的情况考虑到了。

​

总结

1. 状态表示： dp[i][j]表示：[i, j]区间内的所有子序列中，最长的回文子序列的长度
2. 推导状态转移方程： ​
3. 初始化：不用初始化
4. 填表：因为填写dp[i]j]时，可能需要dp[i][j-1], dp[i+1][j], dp[i+1][j-1]，所以从下往上，从左向右
5. 返回值：返回dp[0][n-1]

class Solution 
{
public:
    int longestPalindromeSubseq(string s) 
    {
        int n = s.size();
        //dp[i][j]表示：[i, j]区间内的所有子序列中，最长回文子序列的长度
        vector<vector<int>> dp(n, vector<int>(n));

        for (int i = n - 1; i >= 0; --i)
        {
            for (int j = i; j < n; ++j)
            {
                if (s[i] == s[j])
                {
                    if (i == j)
                        dp[i][j] = 1;
                    else if (i + 1 == j)
                        dp[i][j] = 2;
                    else 
                        dp[i][j] = dp[i+1][j-1] + 2;
                }
                else 
                {
                    dp[i][j] = max(dp[i][j-1], dp[i+1][j]);
                }
            }
        }       
        return dp[0][n-1];
    }
};

1.6 让字符串成为回文串的最少插入次数

题目链接：1312. 让字符串成为回文串的最少插入次数 - 力扣（LeetCode）

​

算法原理：

状态表示

还是和前面一样，根据经验+题目要求，我们可以将dp[i]表示为到达i位置，让[0, i]区间内的字符串变成回文串的最少操作次数，但是这个状态表示是无法推出状态转移方程的，因为dp表中只保存了成为最少操作次数，连回文串我们都无法得知，也就无法推导出dp[i]。

我们可以试一下上一题中，以一段区间来定义状态表示。dp[i][j]表示：让[i,j]区间内的字符串成为回文串的最少操作次数。

状态转移方程

推导状态转移方程，依旧是要根据最近的一步，所以我们主要根据 i 和 j 两个端点来分析问题。

• 1. s[i] == s[j]，这种情况又有三种子情况，1. i == j，也就是说 i 和 j 在同一个位置，那么[i, j]区间构成回文串的最少操作次数就是0（本身就是回文串了）dp[i][j] = 0   2. i + 1 == j，也就是说 i 和 j 紧挨着的，和上面一样dp[i][j] = 0    3.我们需要继续求解[i+1, j-1]这段区间变成回文串的最少次数，dp[i][j] = dp[i+1][j-1]。
• 2. s[i] != s[j]，那么此时有两种方法，让[i, j]区间变成回文串，第一种是在 i 的前面加添加一个字符（该字符的值为s[j]），然后去找[i, j-1]区间，则dp[i][j] = 1 + dp[i][j - 1]；第二种是在 j 的后面添加一个字符（该字符值为s[i]），然后去找[j+1, j]区间，则dp[i][j] = 1 + dp[i+1][j]，最终我们要得到两者的最小值，则dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1。

​

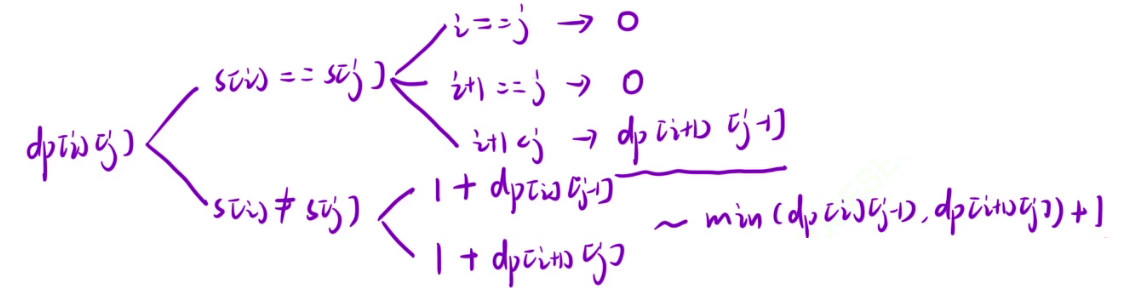
总结

1. 状态表示：dp[i][j]表示：让[i,j]区间内的字符串成为回文串的最少操作次数。
2. 推导状态转移方程：  ​
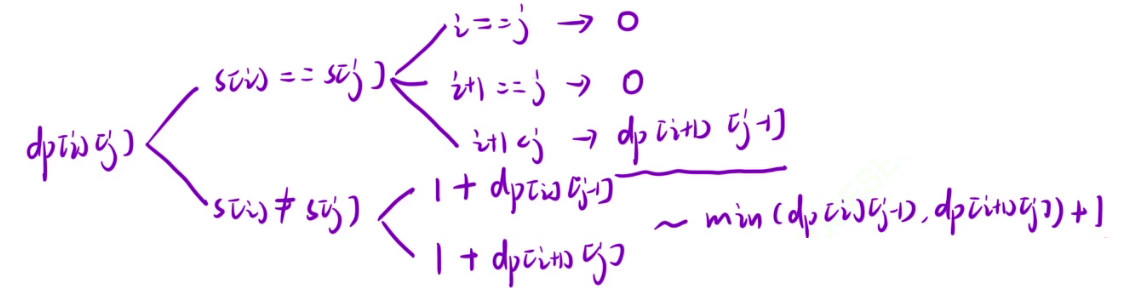
3. 初始化：因为我们默认让 i < j，所以只会用到dp表的右上部分，我们先来考虑s[i] == s[j]的情况，在对角线x中的值一定是0，而对角线y中表示的是(i + 1 == j)，那么也为0，所以s[i] == s[j]的情况不需要初始化，如果s[i] != s[j]，那么就会用到[i][j]位置左和下位置，而y线上的左和下已经初始化过了，所以也不会被干扰，所以这题不需要初始化。​​​​
4. 填表：因为填写dp[i]j]时，可能需要dp[i][j-1], dp[i+1][j], dp[i+1][j-1]，所以从下往上，从左向右
5. 返回值：返回dp[0][n-1]

题解：

class Solution 
{
public:
    int minInsertions(string s) 
    {
        int n = s.size();
        //dp[i][j]表示s的[i, j]区间的字符串变成回文串的最少操作次数
        vector<vector<int>> dp(n, vector<int>(n));

        for (int i = n - 1; i >= 0; --i)
        {
            for (int j = i; j < n; ++j)
            {
                if (s[i] == s[j])
                {
                    if (i == j || i + 1 == j)
                        dp[i][j] = 0;
                    else 
                        dp[i][j] = dp[i+1][j-1];
                }
                else 
                {
                    dp[i][j] = min(dp[i+1][j], dp[i][j-1]) + 1;
                }
            }
        }
        return dp[0][n-1];
    }
};

2. 两个数组的dp问题

在这个问题中，题目通常会给我们两个数组/字符串，通过这两个数组/字符串，找到他们的共性，比如最长公共子序列

面对这类题目，我们通常的解法是：

• 1.选取第一个数组/字符串的[0, i]区间和第二个数组/字符串[0, j]区间作为研究对象
• 2.根据题目要求，定义状态表示
• 3.推导状态转移方程

而两个数组dp问题最经典的就是最长公共子序列，这题可以作为很多题的模板。

2.1 最长公共子序列

题目链接：LCR 095. 最长公共子序列 - 力扣（LeetCode）

​

算法原理：

状态表示

根据经验+题目要求，我们可能会定义以某个位置为结尾的状态表示，比如dp[i][j]表示：在s1中以 i 位置为结尾的所有子序列和s2中以 j 为结尾的子序列中，最长的公共子序列的长度，但是这种状态表示不太好，因为求解一个位置的结尾所有子序列就是一个O(N^2)，如果还要一一枚举i和j的位置，这个算法的时间复杂度将会达到O(N^4)，所以我们尝试以某个区间来定义状态表示。

前面提到过，两个数组的dp问题，通常是选取第一个数组/字符串的[0, i]区间和第二个数组/字符串[0, j]区间作为研究对象，所以我们就可以定义dp[i][j]表示：s1[0, i]区间和s2[0, j]区间的最长公共子序列的长度。

​

状态转移方程

状态转移方程还是要根据最近的一步推导，也就是 i 位置和 j 位置，这两个位置有两种情况。

• 1. s1[i] == s2[j]，那么s1和s2的最长公共子序列一定是以 s1[i] / s2[j] 结尾的，因为这两个字符相同，则在[0, i-1]区间和[0, j-1]区间的最长公共子序列再加这个字符，那还是最长公共子序列。也就是说dp[i][j] = 在s1[0, i-1]和s2[0, j-1]区间最长公共子序列的长度 + 1，即dp[i][j] = dp[i-1][j-1] + 1
• 2. s1[i] != s2[j]，也就是说，如果在s1[0,i]和s2[0, j]区间内能找到最长公共子序列，那么这个子序列不可能同时以s1[i]和s2[j]结尾，最多只能出现其中的一个，那么我们可以去s1[0, i]和s2[0, j-1]中继续判断，也可以去s1[0, i-1]和s2[0, j]中继续判断，最终dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

还有一种可能，两个都不会选，所以去s1[0, i-1]和s2[0, j-1]继续判断，但是在前面两种情况下，是会考虑到这种情况的，为了避免重复计算，所以求dp时就不添加这种情况了。

​

总结

1. 状态表示：dp[i][j]表示：s1[0, i]区间和s2[0, j]区间的最长公共子序列的长度。
2. 推导状态转移方程：   ​
3. 初始化：我们需要考虑到dp[i-1][j-1], dp[i][j-1], dp[i-1][j]等位置，为了防止越界访问，我们额外添加一行和添加一列，表示空串，所以将这一行和这一列都初始化为0，为了让s1和s2的下标映射也统一，所以在s1和s2前面添加一个字符。
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为s1长度，m为s2长度）

题解：

class Solution 
{
public:
    int longestCommonSubsequence(string text1, string text2) 
    {
        int n = text1.size();
        int m = text2.size();
        //dp[i][j]表示text1[0, i]区间和text2[0, j]区间中最长公共子序列的长度
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
        //因为dp表额外添加了一行和一列，那么text1和text2的映射关系就要改变
        //可以在text1和text2前面额外添加一个字符，就不用考虑映射问题了
        text1 = " " + text1;
        text2 = " " + text2;

        //正式填表
        for (size_t i = 1; i < n + 1; i++)
        {
            for (size_t j = 1; j < m + 1; j++)
            {
                if (text1[i] == text2[j])
                    //说明最长公共子序列一定是以text1[i]/text2[j]结尾的，继续去下一个区间内查找
                    dp[i][j] = dp[i-1][j-1] + 1;
                else 
                    //text1[i]和text2[j]不能同时为公共子序列的结尾，所以判断两个区间
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[n][m];
    }
};

2.2 不相交的线

题目链接：1035. 不相交的线 - 力扣（LeetCode）

​

 算法原理：

在求解这道题之前，我们以上图中的示例2来分析一下，结果相当于是从num1中选择[1, 4]和从num2中选择了[1,4]，选择的时候要求两个数组中被选择的数要相同，并且相对位置不能改变，还要求最多。那么这道题和上一道题"最长公共子序列"其实是一样的。

状态表示

前面提到过，两个数组的dp问题，通常是选取第一个数组/字符串的[0, i]区间和第二个数组/字符串[0, j]区间作为研究对象，所以我们就可以定义dp[i][j]表示：num1[0, i]区间和num2[0, j]区间的最长公共子序列的长度。

​

状态转移方程

状态转移方程还是要根据最近的一步推导，也就是 i 位置和 j 位置，这两个位置有两种情况。

• 1. num1[i] == num2[j]，那么num1和num2的最长公共子序列一定是以 num1[i] / num2[j] 结尾的，因为这两个字符相同，则在[0, i-1]区间和[0, j-1]区间的最长公共子序列再加这个字符，那还是最长公共子序列。也就是说dp[i][j] = 在num1[0, i-1]和num2[0, j-1]区间最长公共子序列的长度 + 1，即dp[i][j] = dp[i-1][j-1] + 1
• 2. num1[i] != num2[j]，也就是说，如果在s1[0,i]和s2[0, j]区间内能找到最长公共子序列，那么这个子序列不可能同时以num1[i]和num2[j]结尾，最多只能出现其中的一个，那么我们可以去num1[0, i]和num2[0, j-1]中继续判断，也可以去num1[0, i-1]和num2[0, j]中继续判断，最终dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

还有一种可能，两个都不会选，所以去num1[0, i-1]和num2[0, j-1]继续判断，但是在前面两种情况下，是会考虑到这种情况的，为了避免重复计算，所以求dp时就不添加这种情况了。

​

总结

1. 状态表示：dp[i][j]表示：num1[0, i]区间和num2[0, j]区间的最长公共子序列的长度。
2. 推导状态转移方程：   ​
3. 初始化：我们需要考虑到dp[i-1][j-1], dp[i][j-1], dp[i-1][j]等位置，为了防止越界访问，我们额外添加一行和添加一列，表示空串，所以将这一行和这一列都初始化为0
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为num1长度，m为num2长度）

题解：

class Solution 
{
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) 
    {
        int n = nums1.size();
        int m = nums2.size();

        //dp[i][j]表示：nums1[0, i]区间和nums2[0, j]区间的最长公共子序列的长度。     
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
        //dp额外添加一行一列，注意nums1和nums2下标映射

        for (int i = 1; i < n + 1; i++)
        {
            for (int j = 1; j < m + 1; j++)
            {
                if (nums1[i-1] == nums2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[n][m];
    }
};

2.3 不同的子序列

题目链接：115. 不同的子序列 - 力扣（LeetCode）

算法原理：

状态表示

根据前面两道题的经验，可以发现在两个数组的dp问题中，如果是以某一个位置为结尾来定义状态表示的话，其实很难推导出状态转移方程，所以到这里我们要修改一下策略，我们要选择一段区间作为状态表示。

dp[i][j]表示：s的[0, j]区间内的所有子序列中，有多少个和 t 在[0, i]区间的子串相等。

状态转移方程

状态转移方程需要通过最近的一步来划分，而最近的一步是dp[i][j]是否包含s[j]，这段话的意思是：在s的[0,j]区间的内的子序列要和t[0, i]区间的子串相等的情况下，是否需要s[j]，简而言之就是s的子序列是否以s[j]结尾。

• 1. 以s[j]结尾，则t[i] == s[j]，这两个位置相同，也就是找子序列与他们无关，所以要去s的[0, j-1]区间和t[0, i-1]区间继续查找，即dp[i][j] = dp[i-1][j-1]
• 2. 不以s[j]结尾，那么我们要去s[0, j-1]区间内找到一个k满足，与t[0, i]区间的子串相同的子序列是以s[k]结尾的，所以dp[i][j] = dp[i][j-1]。

第二种情况是一定存在的，但是第一种情况只有t[i] == s[j]的情况下才存在，所以dp[i][j] = dp[i][j-1] + t[i] == s[j] ? dp[i-1][j-1] : 0 

总结

1. 状态表示：dp[i][j]表示：s的[0, j]区间内的所有子序列中，有多少个和 t 在[0, i]区间的子串相等。
2. 推导状态转移方程：dp[i][j] = dp[i][j-1] + t[i] == s[j] ? dp[i-1][j-1] : 0 
3. 初始化：我们需要考虑到dp[i-1][j-1], dp[i][j-1],等位置，为了防止越界访问，我们额外添加一行和添加一列，表示空串，第一行是t为空串的情况，那么s是可以有一个空的子序列的，所以第一行全部初始化为1，第一列是s为空串，s为空则无法推出t，所以第一列为0。
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为t长度，m为s长度）

题解：

class Solution 
{
public:
    int numDistinct(string s, string t) 
    {
        int n = t.size();
        int m = s.size();
        //dp[i][j]表示：s的[0,j]序列中所有的子序列，和t[0,i]区间的子串相同的数量
        vector<vector<double>> dp(n + 1, vector<double>(m + 1, 0));
        //将第一行初始化为1,t为空串的情况，则s能存在空串子序列
        for (int i = 0; i < m + 1; i++)
            dp[0][i] = 1;
        //dp添加一行一列，为了s和t下标映射关系不用改变，在前面添加一个字符
        s = " " + s;
        t = " " + t;

        //正式填表
        for (int i = 1; i < n + 1; i++)
        {
            for (int j = 1; j < m + 1; j++)
            {
                //dp[i-1][j-1]表示:如果和t的子串相同s的子序列是以s[j]结尾
                //dp[i][j-1]表示的是不以s[j]结尾
                //第二种情况一定存在，第一种不一定
                dp[i][j] = dp[i][j-1];
                if (t[i] == s[j])
                    dp[i][j] += dp[i-1][j-1];
            }
        }

        return dp[n][m];
    }
};

2.4 通配符匹配

题目链接：44. 通配符匹配 - 力扣（LeetCode）

算法原理：

状态表示

根据经验+题目要求，这里的经验指的是使用一段区间。

dp[i][j]表示为：p[0, j]区间的子串能否匹配s[0, i]区间的子串。

状态转移方程

我们根据最后一步分情况讨论，也就是说我们根据p串的最后一个位置p[j]位置来判断。

• 1.p[j]是普通字符，如果想和s[0,i]区间子串匹配，至少要满足s[i] = sp[j]，还要满足p[0, j-1]区间能匹配s[0, i-1]区间，所以dp[i][j] = s[i] == s[j] && dp[i-1][j-1] == true。
• 2.p[j]是 ?，那么?是可以匹配任意字符，所以p[j]可以匹配s[i]，接下来我们只要判断p[0, j-1]区间能否匹配s[0, i-1]区间即可，所以dp[i][j] = dp[i-1][j-1] == true。
• 3.p[j]是 * ，p[j]可以匹配任意多个字符
  • (1) *匹配的是空串，也就是说要判断s[0, i]区间和p[0, j-1]区间，所以dp[i][j] = dp[i][j-1] == true
  • (2) *匹配的是一个字符，要判断s[0, i-1]区间和p[0, j-1]区间，所以dp[i][j] = dp[i-1][j-1] == true
  • (3) *匹配的是两个字符，要判断s[0, i-2]区间和p[0, j-1]区间，所以dp[i][j] = dp[i-2][j-1] == true
  • (4) .....

第三种情况，我们有很多种情况，如果把每个情况都查找一次，需要O(N)，那么再加上遍历 i 和 j 位置，那么就需要O(N^3)，时间复杂度很高，我们想一种方法，能否降低时间复杂度，这里用到的方法是使用若干有限个的状态表示去替换原来量级为N的状态表示。

第一种：数学法

在p[j]为 * 时，dp[i][j]可以表示为下面这种形式。

而dp[i-1][j]可以表示为下面这种形式。

仔细观察可以发现，两者有很多重复的地方，如下图划波浪线的地方

我们可以将dp[i][j]中波浪线部分替换成dp[i-1][j]。

所以最终dp[i][j] = dp[i][j-1] || dp[i-1][j]。

第二种：根据实际情况优化

这种方式比较抽象，dp[i][j]如果为空串，那么dp[i][j] = dp[i][j-1]，如果不匹配为空串，那么可以将*匹配一个s[i]，但是匹配完不将这个*舍去，也就是说这个*可以继续和s[i-1], s[i-2]匹配，所以dp[i][j] = dp[i-1][j]。

上面的意思是：根据前面的分析，j位置是一直不变的，只是p[j]匹配的字符个数不同，如果p[j]匹配一个字符时，就会和s[i]配对，那么就要再去s[i-1]中继续判断，前面的做法是p[j]匹配完一个字符就去[j-1]了，所以dp[i][j] = dp[i-1][j-1]，但是如果匹配完不丢弃p[j]位置，也就是说dp[i-1][j]可以继续往下匹配，那么dp[i][j] = dp[i-1][j]，再加上前面空串的情况，则dp[i][j] = dp[i][j-1] || dp[i-1][j]

总结：

初始化

在状态转移方程中，我们需要使用到dp[i][j-1], dp[i-1][j], dp[i-1][j-1]，为了防止越界访问，所以额外添加一行一列表示空串，为了下标映射一致，所以将s和p也额外添加一个字符。

第一行表示的是s为空的情况，p串要想去匹配s串，只有p串是空串或者p串全是*才可以，如果p串有一个非*，则非*后面全为false

第一列表示的是p为空，p为空则无法匹配，全初始化为false。

总结

1. 状态表示：dp[i][j]表示为：p[0, j]区间的子串能否匹配s[0, i]区间的子串
2. 推导状态转移方程：
3. 初始化：额外添加一行一列，s和p前面也添加一个字符，dp表第一行根据p的状态初始化，第一列初始化为false
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为s长度，m为p长度）

题解：

class Solution 
{
public:
    bool isMatch(string s, string p) 
    {
        int n = s.size();
        int m = p.size();

        //dp[i][j]表示为：p[0, j]区间的子串能否匹配s[0, i]区间的子串
        vector<vector<bool>> dp(n + 1, vector(m + 1, false));
        //消除下标错误问题
        s = " " + s;
        p = " " + p;
        //根据p初始化第一行
        dp[0][0] = true;
        for (int i = 1; i < m + 1; i++)
        {
            if (p[i] != '*')
                break;
            dp[0][i] = true;
        }
 
        //填表
        for (int i = 1; i < n + 1; i++)
        {
            for (int j = 1; j < m + 1; j++)
            {
                //如果p[j]是?，则能匹配s[i],去判断s[i-1]
                if (p[j] == '?')
                    dp[i][j] = dp[i-1][j-1];
                //如果p[j]是*，则判断能匹配多少个字符
                else if (p[j] == '*')
                    dp[i][j] = (dp[i][j-1] || dp[i-1][j]);
                //如果p[j]是普通字符，则直接判断
                else 
                    dp[i][j] = (s[i] == p[j] && dp[i-1][j-1]);
            }
        }        

        return dp[n][m];
    }     
};

2.5 正则表达式

题目链接：10. 正则表达式匹配 - 力扣（LeetCode）

这题和上面那题不一样的是，*和前面那个字符是一个整体，比如a*，表示的是0个a，1个a，2个a......。

算法原理：

状态表示

根据经验+题目要求，我们可以将dp[i][j]表示为，p[0, j]区间的子串能否匹配s[0, i]区间的子串。

状态转移方程

我们根据最后一步分情况讨论，也就是说我们根据p串的最后一个位置p[j]位置来判断。

• 1.p[j]是普通字符，如果想和s[0,i]区间子串匹配，至少要满足s[i] = sp[j]，还要满足p[0, j-1]区间能匹配s[0, i-1]区间，所以dp[i][j] = s[i] == s[j] && dp[i-1][j-1] == true。
• 2.p[j]是 '.' ，那么p[j]是可以匹配任意字符，所以p[j]可以匹配s[i]，接下来我们只要判断p[0, j-1]区间能否匹配s[0, i-1]区间即可，所以dp[i][j] = dp[i-1][j-1] == true。
• 3.p[j]是 '*' ，p[j]要和p[j-1]结合起来，所以我们需要判断p[i-1]位置
  • p[j-1]是 '.' ，有下面几种情况
    • (1)此时可以将这两个字符翻译成空串，这时我们就需要判断p[0, j-2]能否匹配s[0, i]区间子串，dp[i][j] = dp[i][j-2]；
    • (2)将这两个字符翻译成一个 '.'，那么就要到s[0, i-1]继续判断，即dp[i][j] = dp[i-1][j-2];
    • (3)将这两个字符翻译成两个 '.'，那么就要到s[0, i-2]继续判断，即dp[i][j] = dp[i-2][j-2];
    • (4)......
  • p[j-1]是普通字符，有两种情况
    • (1)匹配为空串，需要判断p[0, j-2]能否匹配s[0,i]区间，dp[i][j] = dp[i][j-2]。
    • (2)匹配一个字符，此时需要判断这个字符和s[i]是否相同, 还要判断s的[0, i-1]区间子串和p[0, j-2]区间子串能否匹配，dp[i][j] = p[j-1] == s[i] && dp[i-1][j-2] == true
    • (3)匹配两个字符，此时需要判断这个字符和s[i],s[i-1]是否相同, 还要判断s的[0, i-2]区间子串和p[0, j-2]区间子串能否匹配，dp[i][j] = p[j-1] == s[i] == s[i-1] && dp[i-2][j-2] == true
    • (4)......

在p[j]为’*‘，p[j-1]为'.'时，有很多种情况， 如果把每个情况都查找一次，需要O(N)，那么再加上遍历 i 和 j 位置，那么就需要O(N^3)，时间复杂度很高，我们想一种方法，能否降低时间复杂度，这里用到的方法是使用若干有限个的状态表示去替换原来量级为N的状态表示。

第一种：数学法

在p[j]为 * 时，dp[i][j]可以表示为下面这种形式。

如果将上面的 i 全部替换为 i - 1，则dp[i-1][j]可以表示为下面这种形式。

仔细观察可以发现，两者有很多重复的地方，如下图划波浪线的地方

我们可以将dp[i][j]中波浪线部分替换成dp[i-1][j]。

所以最终dp[i][j] = dp[i][j-2] || dp[i-1][j]。

第二种：根据实际情况优化

这种方式比较抽象，我们可以将.*匹配一个s[i]，但是匹配完不将.*舍去，也就是说这个*可以继续和s[i-1], s[i-2]匹配，所以dp[i][j] = dp[i-1][j]，同样，我们可以将.*舍去，也就是说 .*毫无作用，那么dp[i][j] = dp[i][-2]。

上面的意思是：根据前面的分析，j位置是一直不变的，只是 .* 匹配的字符个数不同，如果 .* 匹配一个字符时，就会和s[i]配对，那么配对完就要再去s[i-1]中继续判断，之前的做法是p[j]匹配完一个字符就去[j-1]了，所以dp[i][j] = dp[i-1][j-1]，到了[j-1]还是会重复上面的步骤，所以需要O(N)的时间；优化的做法是匹配完不丢弃 .* ，也就是说dp[i-1][j]可以继续往下匹配，那么dp[i][j] = dp[i-1][j]，再加上直接丢弃.*的情况，则dp[i][j] = dp[i][j-1] || dp[i-1][j]

如果这种方式不太好理解，那么就使用上面那种方法。

p[j]为'*'，p[j-1]为普通字符时和上面是一样的道理，有两种情况，第一种是c*(c表示p[j-1]的字符)直接舍弃不要，那么对应的就是dp[i][j-2]；第二种就是c*匹配一个字符后保留，也就是说c*可以继续匹配s[i-1]，即dp[i-1][j]，但是这种情况下需要保证s[i] == p[j-1]才能成功匹配，所以最终dp[i][j] = dp[i][j-2] || (s[i] == p[j-1] && dp[i-1][j])。

总结：

 初始化

在状态转移方程中，我们需要使用到dp[i][j-1], dp[i-1][j], dp[i-1][j-1]，为了防止越界访问，所以额外添加一行一列表示空串，为了下标映射一致，所以将s和p也额外添加一个字符。

第一行表示的是s为空的情况，p串要想去匹配s串，只有p串是空串或者p串全是(c)*才可以(c表示任意字符)，我们判断p的偶数位，如果出现非*，则此位置开始后面全为false

第一列表示的是p为空，p为空则无法匹配，全初始化为false。

总结

1. 状态表示：dp[i][j]表示为，p[0, j]区间的子串能否匹配s[0, i]区间的子串。
2. 推导状态转移方程： 
3. 初始化：额外添加一行一列，s和p前面也添加一个字符，dp表第一行根据p的状态初始化，第一列初始化为false
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为s长度，m为p长度）

题解：

class Solution 
{
public:
    bool isMatch(string s, string p) 
    {
        int n = s.size();
        int m = p.size();

        //dp[i][j]表示p[0,j]区间子串能否匹配s[0,i]区间子串
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, false));
        //消除下标差值
        s = " " + s;
        p = " " + p;
        //初始化第一行第一列
        dp[0][0] = true;
        for (size_t j = 2; j < m + 1; j += 2)
        {
            if (p[j] == '*')
                dp[0][j] = true;
            else 
                break;
        }

        //填表
        for (size_t i = 1; i < n + 1; i++)
        {
            for (size_t j = 1; j < m + 1; j++)
            {
                if (p[j] == '.')  //如果是. 则匹配当前字符
                    dp[i][j] = dp[i-1][j-1];
                else if (p[j] == '*') //根据p[j-1]进一步判断
                {
                    if (p[j-1] == '.')
                        dp[i][j] = dp[i-1][j] || dp[i][j-2];
                    else 
                        dp[i][j] = dp[i][j-2] || (p[j-1] == s[i] && dp[i-1][j]);
                }
                else //普通字符，直接判断即可 
                    dp[i][j] = (p[j] == s[i] && dp[i-1][j-1]);
            }
        }

        return dp[n][m];
    }
};

2.6 交错字符串

题目链接：LCR 096. 交错字符串 - 力扣（LeetCode）

算法原理：

在这个题目中出现了三个数组，但是我们前面的经验依旧是可以用的，因为如果前面两个数组确定了一段区间，而第三个数组是由前两个组合得到的，所以说第三个数组也就能确定了。

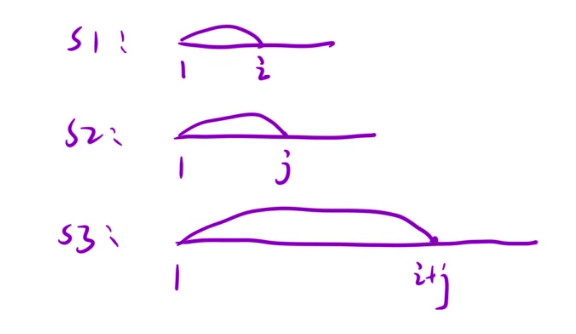
在开始之前，我们需要预处理一下，给s1，s2，s3前面添加一个占位符，保证每个字符串的下标是从1开始的。

状态表示

根据经验+题目要求，dp[i][j]表示为s1[1, i]区间和s2[1,j]区间内的字符串进行交错排列，能否排列成s3[1, i+j]区间子串。

状态转移方程

还是根据最近的一步来推导状态转移方程，最近的一步是处于 i 位置和 j 位置的时候，如果想要s1和s2能拼接成，必须要满足s3[i+j] == s1[i]或者s3[i+j] == s2[j]，因为s3由s1和s3交错拼接的，所以只能由其中一个来结尾。

• 1.s3[i+j] == s1[i]，最后两个字符相等了，我们需要继续判断s1[1,i-1]和s2[1,j]能否拼接成s3[1, i+j-1]，即dp[i-1][j] == true
• 2.s3[i+j] == s2[j]，最后两个字符相等了，我们需要继续判断s1[1,i]和s2[1,j-1]能否拼接成s3[1, i+j-1]，即dp[i][j-1] == true

初始化

dp表需要额外添加一行和一列，第一行第一列表示s1和s2表为空的情况，先来看第一行，第一行表示s1为空，如果想拼接成s3，只能由s2做到，那么s2[1, j]区间内和s3[1, j]区间内对应位置相同初始化为true，只要出现一个不相同的，后面全部为false

再来看第一列，第一列表示s2为空，s2为空则需要s1单独拼接成s3，则s1[1, i]区间内和s3[1, i]区间内对应位置相同初始化为true，只要出现一个不相同的，后面全部为false

总结

1. 状态表示：dp[i][j]表示为s1[1, i]区间和s2[1,j]区间内的字符串进行交错排列，能否排列成s3[1, i+j]区间子串
2. 推导状态转移方程：  
3. 初始化：额外添加一行一列，s1,s2,s3前面添加一个字符，dp表第一行根据s2的状态初始化，第一列根据s1的状态初始化
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j]，所以从上往下，从左向右填表。
5. 返回值：返回dp[n][m] (n为s1长度，m为s2长度）

题解：

class Solution 
{
public:
    bool isInterleave(string s1, string s2, string s3) 
    {
        int n = s1.size();
        int m = s2.size();
        if (n + m != s3.size())
            return false;

        //额外添加一个字符，让下标和dp表对应上
        s1 = " " + s1;
        s2 = " " + s2;
        s3 = " " + s3;

        //创建dp表
        vector<vector<bool>> dp(n + 1, vector<bool>(m + 1, false));
        dp[0][0] = true;
        //初始化第一行
        for (size_t j = 1; j < m + 1; j++)
        {
            if (s2[j] == s3[j])
                dp[0][j] = true;
            else 
                break;
        }
        //初始化第一列
        for (size_t i = 1; i < n + 1; i++)
        {
            if (s1[i] == s3[i])
                dp[i][0] = true;
            else 
                break;
        }

        //填表
        for (size_t i = 1; i < n + 1; i++)
        {
            for (size_t j = 1; j < m + 1; j++)
            {
                dp[i][j] = (s1[i] == s3[i+j] && dp[i-1][j]) 
                        || (s2[j] == s3[i+j] && dp[i][j-1]);
            }
        }

        //返回结果
        return dp[n][m];
    }
};

2.7 两个字符串的最小ASCII删除和

题目链接：712. 两个字符串的最小ASCII删除和 - 力扣（LeetCode）

算法原理：

在做题之前我们可以分析一下，如果要找到删除的ASCII码和最小，那么就相当于是剩下的字符串中ASCII码和最大，所以这题可以转化成，找到两个字符串ASCII码和最大的公共子序列。

状态表示

根据经验+题目要求，我们将dp[i][j]表示为：s1[0,i]区间和s2[0,j]区间的所有的子序列中，ASCII码和最大的公共子序列的ASCII码和。

状态转移方程

推导状态转移方程需要根据最近的一步，最近的一步是 位于 s1的 i 位置和 s2的 j 位置时，那么dp[i][j]有以下四种情况。

• 1.以s1[i]和s2[j]结尾，因为是公共子序列，所以要满足s1[i] == s2[j]，然后还要在s1[0, i-1]区间和s2[0, j-1]区间找到一个ASCII码和最大的公共子序列再加上最后一个字符即可，所以dp[i][j] = dp[i-1][j-1] + s1[i]。
• 2.以s1[i]结尾，也就是说s2[j]位置的值我们不会选择，所以dp[i][j] = dp[i][j-1]
• 3.以s2[j]结尾，也就是说s1[i]位置不会选择，所以dp[i][j] = dp[i-1][j]
• 4.不以s[i]和s2[j]结尾，dp[i][j] = dp[i-1][j-1]，但是这种情况，前两种已经求过了，所以可以忽略

在2中，dp[i][j-1]表示的是s1[0,i]区间所有的子序列，也就是说dp[i][j-1]是包括以s1[i]结尾，也包括不以s1[i]结尾的，所以严格来说dp[i][j] = dp[i][j-1]中间的等号是不正确的，但是题目求的是最大值，所以不会影响结果，第3种也是同理。

总结

1. 状态表示：dp[i][j]表示为：s1[0,i]区间和s2[0,j]区间的所有的子序列中，ASCII码和最大的公共子序列的ASCII码和。
2. 推导状态转移方程：   
3. 初始化：额外添加一行一列，并全部初始化为0
4. 填表：因为填写dp[i][j]时，可能需要dp[i][j-1], dp[i-1][j], dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：要求的是删除最少的ASCII码和，所以我们要求出s1和s2ASCII码总和再减去两倍的dp[n][m] （n为s1的长度，m为s2的长度

题解：

class Solution 
{
public:
    int minimumDeleteSum(string s1, string s2) 
    {
        int n = s1.size();
        int m = s2.size();

        //dp[i][j]表示s1[0,i]区间和s2[0,j]区间的所有子序列中，ASCII码和最大的最长公共子序列的ASCII码和
        vector<vector<int>> dp(n + 1, vector(m + 1, 0));

        //填表
        for (size_t i = 1; i < n + 1; i++)
        {
            for (size_t j = 1; j < m + 1; j++)
            {
                dp[i][j] = max(dp[i-1][j], dp[i][j-1]);

                //如果以s[i]和s[j]结尾，那么要保证s[i]==s[j]
                if (s1[i-1] == s2[j-1])//别忘了下标映射关系
                    dp[i][j] = dp[i-1][j-1] + s1[i-1];
            }
        }

        int sum = 0;
        for (size_t i = 0; i < n; i++)
            sum += s1[i];
        for (size_t j = 0; j < m; j++)
            sum += s2[j];
        return sum - 2 * dp[n][m];
    }
};

2.8 最长重复子数组

题目链接：718. 最长重复子数组 - 力扣（LeetCode）

这道题和最长公共子序列类似，只不过从子序列变成了子数组，相应的难度也会降低。

算法原理：

状态表示

根据经验+状态表示，dp[i][j]可以表示为：nums1[0,i]区间和nums2[0,j]区间内所有的子数组，最长公共子数组长度。

但是这种状态表示的范围太大了，如果说[0, i]区间内的最长子数组是在中间的某一个位置，那么到了i + 1的位置时，不能根据前面的状态来推导当前的dp表（因为可能不连续）。而子序列之所以能使用范围来表示，是因为子序列并不需要保证连续。

dp[i][j]表示：nums1以i位置结尾的所有子数组和nums2以j位置结尾的所有子数组中，最长重复子数组的长度。

状态转移方程

状态转移方程还是根据最后一个位置的情况来推导，也就是nums1的 i 位置和nums2的 j 位置。

• 1.nums1[i] != nums2[j]，则无法得到重复子数组，dp[i][j] = 0
• 2.nums1[i] == nums2[j]，要在nums1找到以[i-1]结尾和nums2以[j-1]结尾的最长的重复子数组，在这个子数组的基础上加上nums1[i] / nums2[j]就是dp[i][j]的最长重复子数组，所以dp[i][j] = dp[i-1][j-1] + 1。

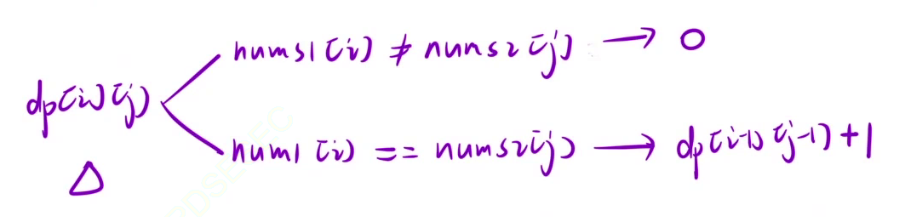
总结

1. 状态表示：dp[i][j]表示：nums1以i位置结尾的所有子数组和nums2以j位置结尾的所有子数组中，最长重复子数组的长度。
2. 推导状态转移方程：    
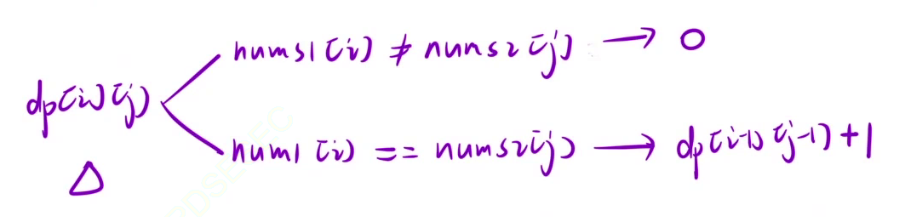
3. 初始化：额外添加一行一列，并全部初始化为0
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j-1]，所以从上往下，从左向右填表。
5. 返回值：返回整个表的最大值。

题解：

class Solution 
{
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) 
    {
        int n = nums1.size();      
        int m = nums2.size();

        //dp[i][j]表示：nums1以i位置结尾的所有子数组和nums2以j位置
        //结尾的所有子数组中，最长重复子数组的长度。
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));

        int ret = 0;
        for (size_t i = 1; i < n + 1; i++)
        {
            for (size_t j = 1; j < m + 1; j++)
            {
                if (nums1[i-1] == nums2[j-1])
                {
                    dp[i][j] = dp[i-1][j-1] + 1;
                    ret = max(ret, dp[i][j]);
                }
                else 
                {
                    dp[i][j] = 0;
                }
            }
        }
        return ret;
    }
};

3.背包问题

背包问题是动态规划中非常重要的一个模型，不管是在比赛还是笔试面试中都是常考题，并且背包问题的分类也有很多，有些难度太大的在这里就不讲了，本文只讲01背包和完全背包，以及这两种情况的变形问题。

背包问题指的是：有一些商品，我们需要挑选一些商品，使得背包内的商品价值最大。背包问题难就难在商品和背包都是有属性的，比如商品会有体积和价值，背包是有容量限制的。

比如上图中，背包容量是6，每个商品的体积和价值如上所示。

而根据每个商品的个数，又可以将背包问题划分成01背包问题（每个商品只有一个），完全背包问题（每个商品的数量没有限制）。

同样根据背包，也可以添加限制条件，1.背包不必完全装满，2.背包必须装满。

3.1 01b背包

3.1.1 01背包

题目链接：【模板】01背包_牛客题霸_牛客网

算法原理：

状态表示

背包问题本质上还是线性dp问题，所以我们依旧可以根据前面的经验（以某个位置结尾.....）来定义状态表示。

dp[i]表示：从前 i 个物品中，所有的选法中，能挑选出来的最大价值。

但是只有上面这个是推导不出状态转移方程的，因为我们还需要考虑容量问题，在挑选出最大价值后，我们还需要保证这个选法的容量不会超过背包的容量。

dp[i][j]表示：从前 i 个物品中挑选，使得总体积不能超过 j ，所有选法中，能挑选出的最大价值。

由于这道题有两问，第二问的问题是总体积正好为V的时候，那么只需要在上面的基础上个稍加修改即可。

dp[i][j]表示：从前 i 个物品中挑选，使得总体积正好为 j ，所有选法中，能挑选出的最大价值

状态转移方程

先推导第一问的状态转移方程，推导状态转移方程还是和前面一样，根据最后一步来推导，最后一步有两种情况。

• 1.选择第 i 个物品，接下来我们就去前 i - 1 个物品中挑选一个价值最大选法，但是第 i 个物品也是有体积的，假设体积为vi，要找到一个总体积小于j - vi的选法，所以我们在[1, j-1]中要挑选一个体积小于j - vi的价值最大的方法，所以dp[i][j] = wi + dp[i-1][j-vi]（j - vi可能会小于0发生越界访问，所以要满足 j - vi >= 0）。
• 2.不选择第 i 个物品，不选择 i 的话，那么dp[i][j]就是去[1, i-1]中选择价值最大的，所以dp[i][j] = dp[i-1][j]。

上面两种情况都有可能出现，所以要去两者最大值，dp[i][j] = max(dp[i-1][j], wi + dp[i-1][j-vi])。

 

第二问的状态转移方程和第一问是一样的，只不过需要注意，dp[i-1][j]不是会一定存在的，如果dp[i-1][j]不存在，则dp[i][j]也不存在，因为要满足总体积恰好等于j，我们让dp[i][j] == -1表示不存在，但是不选择第 i 个商品的dp[i][j] = dp[i-1][j]是不需要改变的，因为如果dp[i-1][j] == -1（不存在）那么dp[i-1][j]也等于 -1，表示不存在

接下来我们需要看选择第 i 个商品的情况，和上面一样，我们也要判断dp[i-1][j-v[i]]是否存在，只有存在了，才能在他的基础上加上第 i 个商品。

绿色部分是第二问比第一问多出来需要判断的。

总结

1. 状态表示：
   • dp1[i][j]表示：从前 i 个物品中挑选，使得总体积不能超过 j ，所有选法中，能挑选出的最大价值。
   • dp2[i][j]表示：从前 i 个物品中挑选，使得总体积正好为 j ，所有选法中，能挑选出的最大价值
2. 推导状态转移方程：     
3. 初始化：额外添加一行一列，dp1全部初始化为0，dp2第一行除了dp2[0][0]全部初始化为-1。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i-1][j-v[i]]所以从上往下填表。
5. 返回值：返回dp1[n][v]和max(0, dp2[n][V])。

题解：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1001;
int n, V;
int v[N];
int w[N];
int dp[N][N];

int main() 
{
    cin >> n >> V;
    for (size_t i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    //解决第一问
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            dp[i][j] = dp[i-1][j]; //不选择第i个商品
            if (j - v[i] >= 0) 
                dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]] + w[i]); //选择第i个商品
        }
    }
    cout << dp[n][V] << endl;

    //解决第二问
    memset(dp, 0, sizeof(dp));
    //初始化第一行
    for (size_t j = 1; j <= V; j++)
        dp[0][j] = -1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            dp[i][j] = dp[i-1][j];
            if (j - v[i] >= 0 && dp[i-1][j-v[i]] != -1)
                dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]] + w[i]);
        }
    }
    cout << max(0, dp[n][V]);

    return 0;
}
// 64 位输出请用 printf("%lld")

优化：

在求解背包问题时，可以通过滚动数组优化来减少时间和空间复杂度。

这是原始的二维dp表。

我们在填写dp[i][j]（上面圆圈的位置）时，只需要知道dp[i-1][j]和dp[i][j-v[i]]（上面三角的位置），也就是说，其他位置的值我们根本不需要了，所以我们可以将二维数组优化成一维的，现在我们只需要两个滚动数组。

有了第一个数据，那么我们就能填写好第二个数组，填写好第二个数组之后，第一个数组就没有用了，此时我们可以进行滚动，把第一个数组移动到第二个数组下面

如果觉得两个滚动数组太多了，我们甚至可以只使用一个滚动数组，也就是最终只有一个dp[j]（i下标不存在了）

当我们之前填写dp[i][j]时，需要dp[i-1][j]和dp[i-1][j-v[i]]，那么现在我们填写dp[j]时，需要dp[j]和dp[j-v[i]]，如果采用了这种方式，我们只能从右向左填表，否则会将旧值覆盖掉，影响最终结果。

题解：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1001;
int n, V;
int v[N];
int w[N];
int dp[N]; 

int main() 
{
    cin >> n >> V;
    for (size_t i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    //解决第一
    for (int i = 1; i <= n; i++)
    {
        //j一直在变小，出现一个小于0的，后面都小于0，所以直接结束
        //所以将j-v[i]>=0放到判断逻辑里面即可 
        for (int j = V; j >= v[i]; --j) //修改遍历顺序
        {
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[V] << endl;

    //解决第二问
    memset(dp, 0, sizeof(dp));
    //初始化第一行
    for (int j = 1; j <= V; j++)
        dp[j] = -1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = V; j >= v[i]; --j) //修改遍历顺序
        {
            if (dp[j - v[i]] != -1)
                dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << max(0, dp[V]);

    return 0;
}
// 64 位输出请用 printf("%lld")

3.1.2 分割等和子集

题目链接：416. 分割等和子集 - 力扣（LeetCode）

算法原理：

如果说原数组的所有数之和为sum，那么两个子集的元素和应该都是sum / 2，而我们只需要找到一个集合中的元素和为sum / 2即可。

那么上面这个问题就转化成了，从原数组中选取一些数，使得这些数的总和为sum / 2，而这种模型和01背包是非常相似的，可以看成每个物品都有价格，背包中的容量为sum / 2，要将背包完全装满。

状态表示

根据上一题01背包的经验+题目要求，我们可以直接定义状态表示。

dp[i][j]表示：从前 i 个元素中选，所有的选法中，能否凑成 j 这个数。

状态转移方程

在第 i 个数时，有两种情况。

• 1.不选择第 i 个数，那么就要去前 i - 1个数中，找到能否凑成 j 的选法，即dp[i][j] = dp[i-1][j]。
• 2.选择第 i 个数，要使总和为 j，那么就去前 i - 1个数中凑到 j - nums[i]，即dp[i][j] = dp[i-1][j-nums[i]]（j - nums[i]不一定存在，需要判断一下是否大于等于0，否则会越界）

上面这两种选法，只要有一种情况存在即可，所以dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]。

总结

1. 状态表示：dp[i][j]表示：从前 i 个元素中选，所有的选法中，能否凑成 j 这个数
2. 状态转移方程： dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]
3. 初始化：额外添加一行一列，第一列全为true，第一行除了dp[0][0]全部初始化为false。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i-1][j-nums[i]]所以从上往下填表。
5. 返回值：返回dp[n][sum / 2]。

题解：

class Solution 
{
public:
    bool canPartition(vector<int>& nums) 
    {
        //求nums的总和
        int sum = 0;
        for (auto e : nums)
            sum += e;
        //如果sum为奇数，则无法分割成两个子集
        if (sum % 2 != 0)
            return false;
        
        int n = nums.size();
        int target = sum / 2;
        //dp[i][j]表示：从前i给数中挑选任意个数，能否使得这些数的总和为j
        vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));
        //将第一列初始化为true
        for (size_t i = 0; i <= n; i++)
            dp[i][0] = true;

        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= target; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - nums[i-1] >= 0)
                    dp[i][j] = dp[i][j] || dp[i-1][j-nums[i-1]];
            }
        }
        return dp[n][sum / 2];
    }
};

优化：

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维，然后让数组的遍历方向从后往前即可。

class Solution 
{
public:
    bool canPartition(vector<int>& nums) 
    {
        //求nums的总和
        int sum = 0;
        for (auto e : nums)
            sum += e;
        //如果sum为奇数，则无法分割成两个子集
        if (sum % 2 != 0)
            return false;
        
        int n = nums.size();
        int target = sum / 2;
        //dp[i][j]表示：从前i给数中挑选任意个数，能否使得这些数的总和为j
        vector<bool> dp(target + 1, false);
        dp[0] = true;

        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = target; j >= nums[i-1]; j--)
            {
                dp[j] = dp[j] || dp[j-nums[i-1]];
            }
        }
        return dp[target];
    }
};

3.1.3 目标和

题目链接：LCR 102. 目标和 - 力扣（LeetCode）

算法原理：

这道题不能直接用动态规划做，因为状态表示不好定义，我们可以先转换一下，原数组nums，我们可以将里面的数分为两类，一类是正数，一类是负数，如果所有正数和为a，所有负数和的绝对值为b，那么a - b = target，但是此时依旧有两个未知数，还是麻烦。

我们再假设原数组所有数之和为sum，那么a + b = sum。通过上面两个式子，我们能得到2 * a = target + sum，即 a = (target + sum) / 2。

所以说我们不用关心负数集合，那么原问题就变成了从原数组中选择一些数，让这些数之和为a((target + sum) / 2)有多少种选法。

所以这题其实就是一个01背包问题，可以原数组中的值看成商品的价格，背包的容量为(target + sum) / 2，必须要把背包装满，一共有多少种选法。

状态表示

dp[i][j]表示为：从前 i 个数中任意选择，使得这些数的总和正好为 j ，一共有多少种选法。

状态转移方程

在第 i 个数时，有两种情况。

• 1.不选择第 i 个数，那么就要在前面 i - 1个数中选择总和为j的，即dp[i][j] = dp[i-1][j]。
• 2.选择第 i 个数，要使总和为j，则在前面 i - 1 个数中要选择总和为 j - nums[i]的，在这些选法的后面添加nums[i]即可，所以dp[i][j] = dp[i-1][j-nums[i]]（注意不用添加 + nums[i]，因为这里问的是选法，选择第 i 个数只是在前面的选法中添加一个数，并不会改变总的选法数）同样，这里的j - nums[i]也不一定存在，需要判断j - nums[i]是否大于等于0。

这两种情况都有可能，所以最终dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]。

总结

1. 状态表示：dp[i][j]表示为：从前 i 个数中任意选择，使得这些数的总和正好为 j ，一共有多少种选法。
2. 推导状态转移方程：dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]]。
3. 初始化：额外添加一行一列，dp[0][0]为true，第一行除了dp[0][0]全部初始化为false，第一列是j为0的情况，j为0是有可能存在的，我们需要计算一下，但是计算的过程可以放到填表的地方，所以第一列除了dp[0][0]，其他不用初始化。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i-1][j-nums[i]]所以从上往下填表。
5. 返回值：返回dp[n][a]。（a = （target + sum）/ 2 ）。

题解：

class Solution 
{
public:
    int findTargetSumWays(vector<int>& nums, int target) 
    {
        //整个数组为nums，若数组可以划分成正数集合和负数集合，正数总和为a，负数绝对值总和为b
        //那么a - b = target， 又a + b = sum
        //所以a = (sum + target) / 2，所以和负数是无关的，即我们不需要关心符号问题
        //只要在原数组中任意选则，使得总和为(sum + target) / 2即可。

        //求总和
        int sum = 0;
        for (auto e : nums)
            sum += e;
        int n = nums.size();

        //创建dp表
        int a = (sum + target) / 2;
        //需要特判一下，如果(sum + target)是奇数或者为负数都无法得出结果
        if ((sum + target) % 2 != 0 || a < 0)
            return 0;
        vector<vector<int>> dp(n + 1, vector<int>(a + 1, 0));
        dp[0][0] = 1;

        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = 0; j <= a; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - nums[i-1] >= 0)
                    dp[i][j] += dp[i-1][j-nums[i-1]];
            }
        }
        return dp[n][a];
    }
};

优化：

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维，然后让数组的遍历方向从后往前即可。

class Solution 
{
public:
    int findTargetSumWays(vector<int>& nums, int target) 
    {
        //整个数组为nums，若数组可以划分成正数集合和负数集合，正数总和为a，负数绝对值总和为b
        //那么a - b = target， 又a + b = sum
        //所以a = (sum + target) / 2，所以和负数是无关的，即我们不需要关心符号问题
        //只要在原数组中任意选则，使得总和为(sum + target) / 2即可。

        //求总和
        int sum = 0;
        for (auto e : nums)
            sum += e;
        int n = nums.size();

        //创建dp表
        int a = (sum + target) / 2;
        //需要特判一下，如果(sum + target)是奇数或者为负数都无法得出结果
        if ((sum + target) % 2 != 0 || a < 0)
            return 0;
        vector<int> dp(a + 1, 0);
        dp[0] = 1;

        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = a; j >= nums[i-1]; j--)
            {
                dp[j] += dp[j-nums[i-1]];
            }
        }
        return dp[a];
    }
};

3.1.4 最后一块石头的重量II

题目链接：1049. 最后一块石头的重量 II - 力扣（LeetCode）

算法原理：

这题的难点在于如何将题目转化为动态规划的思想，假如有[a,b,c,d,e]几个数

第一次我们选择b,d两个数碰撞，得到[a, b-d, c, e]（b > d）

第二次选择a，c进行碰撞，得到[b-d, c-a, e]（c > a）

如上选择几次，最终我们能得到一个数[e-b+d+c-a]。

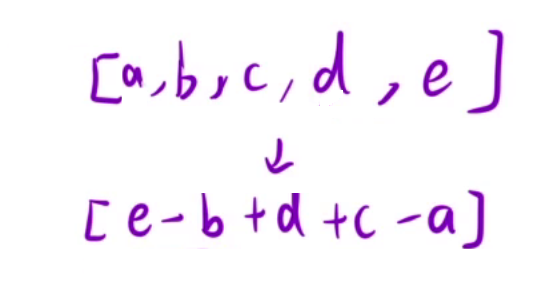
这个数组就是在原来的数组中，给每个数前面添加一个正号或者负号得到的结果。

那么这题和上一题就是一样的了，将原数组划分成两个部分，第一个部分正数（原数组中添加正号）集合，第二个部分是负数（原数组中添加负号）集合，设a为正数总和，b为负数绝对值之和，那么题目的要求就是使得 |a - b| 最小。

已知a + b == sum，如果要使 |a - b| 最小，那么让a和b的取值越接近sum / 2。因为有了a我们就能得到b（sum - a == b），所以我们就只去找a数组即可。

所以这道题可以转化为：在数组中选择一些数，使得这些数的和尽可能接近sum / 2。

状态表示

dp[i][j]表示：从前 i 个数中选择，总和不超过 j ，此时的最大和。

因为我们要找到的不超过 sum / 2的最大和，所以此时的a数组一定是小于等于b数组的，所以最终返回的是b - a。

状态转移方程

在第 i 个数时，我们有两种选择。

• 1.不选择第 i 个数，那么我们就要去前 i - 1 个数中找到总和不超过j的，所以dp[i][j] = dp[i-1][j]。
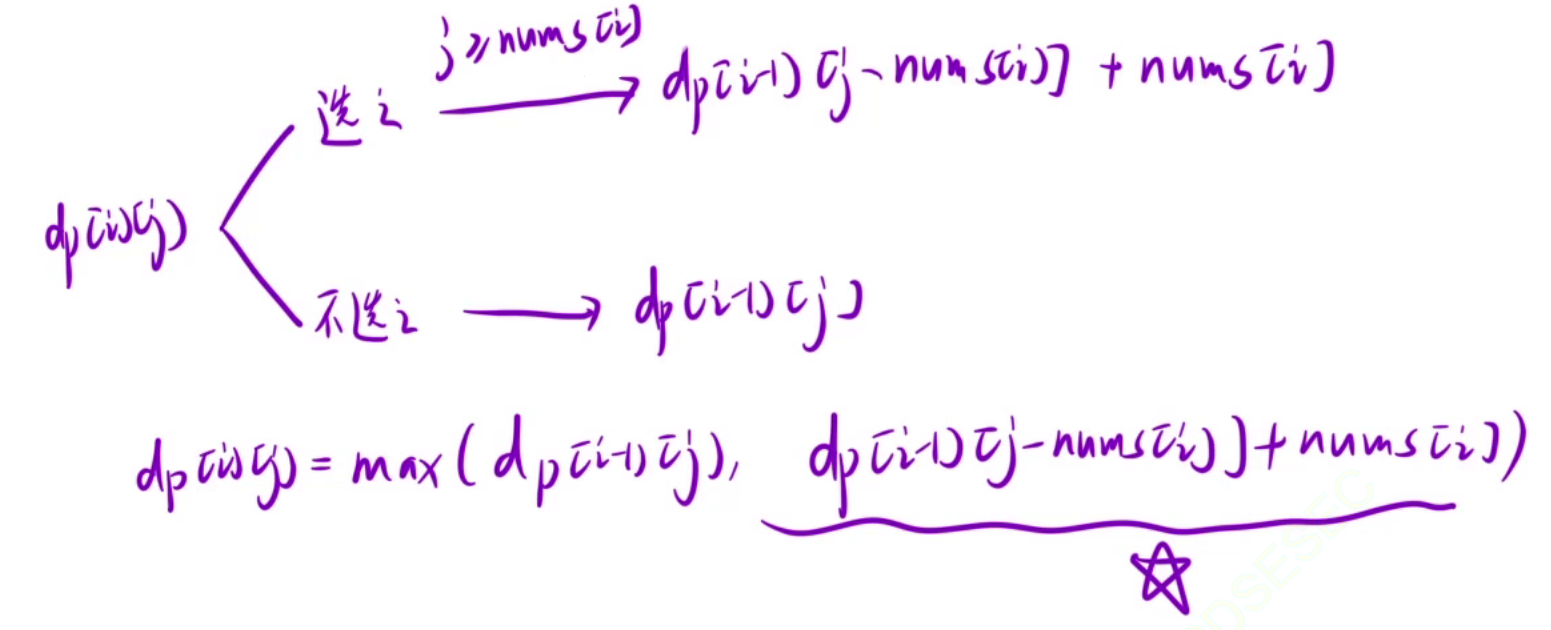
• 2.选择第 i 个数，要使总和不超过j，那么就去前面i - 1个数找到总和不超过j - nums[i]的，所以dp[i][j] = dp[i-1][j-nums[i]] + nums[i]（需要注意j - nums[i]可能不存在，所以需要判断一下，j-nums[i]要大于等于0。

上面两种情况都有可能，所以最终dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])。

总结

1. 状态表示：dp[i][j]表示：从前 i 个数中选择，总和不超过 j ，此时的最大和。
2. 推导状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])。 
3. 初始化：额外添加一行一列，第一行全初始化为0即可，第一列不用管，因为在填表时，会自动填好。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i-1][j-nums[i]]所以从上往下填表。
5. 返回值：dp[n][sum/2]表示的是a，sum-dp[n][sum/2]表示的是b，最小值即为b - a，即sum - 2 * dp[n][sum/2]。

题解：

class Solution 
{
public:
    int lastStoneWeightII(vector<int>& stones) 
    {
        //转化成01背包问题
        //在数组中选取一些数，使得这些数之和尽可能接近sum / 2
        int sum = 0;
        int n = stones.size();
        for (auto e : stones)
            sum += e;
        int target = sum / 2;

        //dp[i][j]表示：前i个数中选取几个数，总和不超过j，此时的最大和。
        vector<vector<int>> dp(n + 1, vector<int>(target + 1, 0));
        
        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = 0; j <= target; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - stones[i-1] >= 0)
                    dp[i][j] = max(dp[i][j], dp[i-1][j-stones[i-1]] + stones[i-1]);
            }
        }

        //sum - dp[n][target]为b dp[n][target]为a
        //则最终结果b-a为sum - 2*dp[n][target];
        return sum - 2 * dp[n][target];
    }
};

优化：

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维，然后让数组的遍历方向从后往前即可。

class Solution 
{
public:
    int lastStoneWeightII(vector<int>& stones) 
    {
        //转化成01背包问题
        //在数组中选取一些数，使得这些数之和尽可能接近sum / 2
        int sum = 0;
        int n = stones.size();
        for (auto e : stones)
            sum += e;
        int target = sum / 2;

        //dp[i][j]表示：前i个数中选取几个数，总和不超过j，此时的最大和。
        vector<int> dp(target + 1, 0);
        
        //填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = target; j >= stones[i-1]; j--)
            {
                dp[j] = max(dp[j], dp[j-stones[i-1]] + stones[i-1]);
            }
        }

        //sum - dp[n][target]为b dp[n][target]为a
        //则最终结果b-a为sum - 2*dp[n][target];
        return sum - 2 * dp[target];
    }
};

最终也是击败了100%的用户

3.2 完全背包

3.2.1 完全背包

题目链接：【模板】完全背包_牛客题霸_牛客网

完全背包就是在01背包的基础上，修改一个条件：每个物品的数量是无限的。

算法原理：

状态表示

状态表示和01背包的状态表示是一样的，dp1[i][j]表示：从前 i 个物品中选，使得总体积不超过 j ，所有的选法中最大的价值。

第二问要让背包一定装满，所以dp2[i][j]表示：从前 i 个物品中选，使得总体积为 j，所有的选法中最大的价值。

状态转移方程

在到达第 i 个物品时，有一些几种情况：

• 1.不选择第 i 个物品，则我们需要去前 i - 1个物品中挑选出总体积不超过j的，所以dp[i][j] = dp[i-1][j]。
• 2.选1个 i 物品，要使总体积不超过j，那么就要去前i - 1个物品中挑选总体积不超过j-v[i]，所以dp[i][j] = dp[i-1][j-v[i]] + w[i]。
• 3.选2个 i 物品，要使总体积不超过j，就要去前i-1个物品中挑选总体积不超过j - 2*v[i]，所以dp[i][j] = dp[i-1][j-2*v[i]] + 2*w[i]。
• 4.选3个 i 物品，要使总体积不超过j，就要去前i-1个物品中挑选总体积不超过j - 3*v[i]，所以dp[i][j] = dp[i-1][j-3*v[i]] + 3*w[i]。
• 5.........

每一种情况都有可能，所以最终取得是上面所有情况的最大值。

在完全背包问题中，选择多少个第 i 个物品是不能确定的，所以我们需要将所有情况都考虑一遍我需要O(N)的时间复杂度，那么再加上遍历 i 和 j，那么就需要O(N^3)，时间复杂度很高，我们想一种方法，能否降低时间复杂度，这里用到的方法是数学法（可以参考“通配符匹配”和“正则表达式”这两题）

我们可以将上面得出的结论转化成表达式，（k表示最多能选k个物品）

如果我将 j 全部替换为 j - v[i]。

此时我们要判断k能否等于x，我们要让j - kv[i]无限接近于0，j - xv[i]也是无限接近于0的，那么仔细观察dp[i-1][j-kv[i]]，dp[i-1][j-xv[i]]，要想都无限接近于0，只能是x == k。

通过观察，我们发现下面那个式子比上面那个式子少一个w[i]，所以我们可以给下面的式子统一加一个w[i]后，就可以替换掉上面波浪线的部分，所以最终dp[i][j] = max(dp[i-1][j], dp[i][j-v[i]] + w[i])

---

---

接下里我们推导第二问的状态转移方程，因为题目要求总体积必须为 j，所以会有总体积无法为j的情况，我们让dp[i][j] = -1表示在前i个中选，不存在总体积为j。

那么我们在第一问推导出dp[i][j] = max(dp[i-1][j], dp[i][j-v[i]] + w[i])的情况下，需要判断一下，前一个数是否存在。如果是dp[i-1][j]其实不用判断，因为如果dp[i-1][j]不存在，那么dp[i][j]也不存在，但是dp[i][j-v[i]]就需要判断一下了，如果dp[i][j-v[i]]=-1不存在，那么我们因为不能以他为基础添加w[i]，因为加上w[i]后，dp[i][j]可能就大于0了，又变成存在了，这显然不合理。

对比一下01背包的状态转移方程，可以看到基本上是一样的，就是把dp[i-1][j-v[i]变成了dp[i][j-v[i]]

总结

1. 状态表示：
   1. dp1[i][j]表示：从前 i 个物品中选，使得总体积不超过 j ，所有的选法中最大的价值
   2. dp2[i][j]表示：从前 i 个物品中选，使得总体积为 j，所有的选法中最大的价值
2. 推导状态转移方程：绿色部分为第二问要多添加的判断条件
3. 初始化：dp1和dp2额外添加一行一列，dp1第一行全初始化为0即可，第一列不用管，因为在填表时，会自动填好，dp2第一行除了dp2[0][0]为true，其他为false（因为无法从前0个数找到总体积为1，2，3......
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i][j-v[i]]所以从上往下，从左往右填表。
5. 返回值：dp1[n][V]，max(0, dp2[n][V])。

题解：

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 1001;
int n, V;
int v[N];
int w[N];
int dp[N][N];

int main() 
{
    cin >> n >> V;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    
    //第一问
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            dp[i][j] = dp[i-1][j];
            if (j-v[i] >= 0)
                dp[i][j] = max(dp[i][j], dp[i][j-v[i]] + w[i]);
        }
    }
    cout << dp[n][V] << endl;

    //第二问
    memset(dp, 0, sizeof(dp));
    for (int j = 1; j <= V; j++)
        dp[0][j] = -1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            dp[i][j] = dp[i-1][j];
            if (j-v[i] >= 0 && dp[i][j-v[i]] != -1)
                dp[i][j] = max(dp[i][j], dp[i][j-v[i]] + w[i]);
        }
    }
    cout << max(0, dp[n][V]) << endl;

    return 0;
}

优化：

背包问题在优化时通常都是使用滚动数组，做空间上的优化，从而对时间上也能优化。

这是原始的二维dp表。

我们在填写dp[i][j]（上面圆圈的位置）时，只需要知道dp[i-1][j]和dp[i][j-v[i]]（上面三角的位置），也就是说，其他位置的值我们根本不需要了，所以我们可以将二维数组优化成一维的，现在我们只需要两个滚动数组。

有了第一个数据，那么我们就能填写好第二个数组，填写好第二个数组之后，第一个数组就没有用了，此时我们可以进行滚动，把第一个数组移动到第二个数组下面

如果觉得两个滚动数组太多了，我们甚至可以只使用一个滚动数组，也就是最终只有一个dp[j]（i下标不存在了）

当我们之前填写dp[i][j]时，需要dp[i-1][j]和dp[i][j-v[i]]，那么现在我们填写dp[j]时，需要dp[j]和dp[j-v[i]]，如果采用了这种方式，我们只能从左往右填表，否则会将旧值覆盖掉，影响最终结果。

注意这里要区分和01背包的区别，完全背包优化是从左往右，而01背包的优化是从右往左。

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 1001;
int n, V;
int v[N];
int w[N];
int dp[N];

int main() 
{
    cin >> n >> V;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    
    //第一问
    for (int i = 1; i <= n; i++)
    {
        for (int j = v[i]; j <= V; j++)
        {
            dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
        }
    }
    cout << dp[V] << endl;

    //第二问
    memset(dp, 0, sizeof(dp));
    for (int j = 1; j <= V; j++)
        dp[j] = -1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = v[i]; j <= V; j++)
        {
            if (dp[j-v[i]] != -1)
                dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
        }
    }
    cout << max(0, dp[V]) << endl;

    return 0;
}

3.2.2 零钱兑换

题目链接：322. 零钱兑换 - 力扣（LeetCode）

这个题就是一道典型的完全背包问题。

算法原理：

状态表示

状态表示和完全背包那里是一样的。dp[i][j]表示：从前 i 个硬币中挑选，使得硬币的总和正好等于 j，所有的选法中，最少的硬币个数。

状态转移方程

还是根据最后一步来推导状态转移方程，即到达第 i 个硬币时，有以下几种情况。

• 1.不选择第 i 个硬币，那么就要在前面 i - 1个硬币中凑到总和为j，所以dp[i][j] = dp[i-1][j]。
• 2.选择1个第 i 个硬币，要使总和为 j，那么就要在前面 i - 1个硬币中凑到总和为j - coins[i]，在前面的基础上加上第 i 个硬币，所以dp[i][j] = dp[i-1][j-coinst[i]] + 1。
• 3.选择2个第 i 个硬币，要使总和为 j，那么就要在前面 i - 1个硬币中凑到总和为j - 2*coins[i]，在前面的基础上加上两枚第 i 个硬币，所以dp[i][j] = dp[i-1][j-2*coinst[i]] + 2。
• 4........

在完全背包问题中，选择多少个第 i 个物品是不能确定的，所以我们需要将所有情况都考虑一遍需要O(N)的时间复杂度，那么再加上遍历 i 和 j，那么就需要O(N^3)，时间复杂度很高，我们想一种方法，能否降低时间复杂度，这里和上面完全背包那题的思路是一样的，采用数学法，将j - coins[i]替换 j，就能得到dp[i][j] = dp[i][j - coins[i]] + 1。

那么最终我们要对上面的情况取最小值，所以dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)

记得要满足 j - coinst[i] >= 0，否则会发生越界访问。

初始化

在填写dp表，我们会用到dp[i-1][j]和dp[i][j-coins[i]]，所以我们额外添加一行一列，保证不会发生越界，我们将dp[0][0]初始化为0，但是dp[0][1],dp[0][2],dp[0][3].....，这些值应该都是不存在的值，而为了不影响结果，我们可以将这些位置初始化为无穷大（这里的无穷大最好不要设置为INT_MAX，而是0x3f3f3f3f，因为前者在+1后会越界，在有些编译器中会直接报错，而后者是前者的一半，也是无穷大的，但是基本上不会发生越界的情况。

总结

1. 状态表示：dp[i][j]表示：从前 i 个硬币中挑选，使得硬币的总和正好等于 j，所有的选法中，最少的硬币个数。
2. 推导状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)
3. 初始化：额外添加一行一列，第一行除了dp[0][0]，其他全部初始化为0x3f3f3f3f。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i][j-coins[i]]所以从上往下，从左往右填表。
5. 返回值：dp[n][amount] >= INF ? -1 : dp[n][amount]（dp在计算过程中，可能会让dp[n][amout]的值大于等于INF(0x3f3f3f3f)，这个值表示不存在的情况，题目要求不存在返回-1，所以要判断一下）。

题解：

class Solution 
{
public:
    int coinChange(vector<int>& coins, int amount) 
    {
        int n = coins.size();
        int INF = 0x3f3f3f3f;
        //创建dp表
        //dp[i][j]表示：从前i个硬币中挑选，总和为j，所有选法中最少的硬币个数
        vector<vector<int>> dp(n + 1, vector<int>(amount + 1, 0));
        for (int j = 1; j <= amount; j++)
            dp[0][j] = INF;

        //开始填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= amount; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - coins[i-1] >= 0)
                    dp[i][j] = min(dp[i][j], dp[i][j-coins[i-1]] + 1);
            }
        }

        //判断返回值
        return dp[n][amount] >= INF ? -1 : dp[n][amount];
    }
};

优化

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维即可，甚至都不需要改变遍历方向。

class Solution 
{
public:
    int coinChange(vector<int>& coins, int amount) 
    {
        int n = coins.size();
        int INF = 0x3f3f3f3f;
        //创建dp表
        //dp[i][j]表示：从前i个硬币中挑选，总和为j，所有选法中最少的硬币个数
        vector<int> dp(amount + 1, INF);
        dp[0] = 0;
        //开始填表
        for (int i = 1; i <= n; i++)
        {
            for (int j = coins[i-1]; j <= amount; j++)
            {
                dp[j] = min(dp[j], dp[j-coins[i-1]] + 1);
            }
        }

        //判断返回值
        return dp[amount] >= INF ? -1 : dp[amount];
    }
};

3.2.3 零钱兑换II

题目链接：518. 零钱兑换 II - 力扣（LeetCode）

这道题和上道题几乎是一样的，只是换了种问法。

算法原理：

状态表示

dp[i][j]表示：从前 i 个硬币中挑选，使得硬币的总和正好等于 j ，一共有多少种选法。

状态转移方程

还是根据最后一步来推导状态转移方程，即到达第 i 个硬币时，有以下几种情况。

• 1.不选择第 i 个硬币，那么就要在前面 i - 1个硬币中凑到总和为j，所以dp[i][j] = dp[i-1][j]。
• 2.选择1个第 i 个硬币，要使总和为 j，那么就要在前面 i - 1个硬币中凑到总和为j - coins[i]，在前面的基础上加上第 i 个硬币，所以dp[i][j] = dp[i-1][j-coins[i]]（这里不需要添加1或者coinst[i]，因为我们的状态表示是总选法数，我们只是在前面的选法中额外添加一枚硬币，总的选法数不会改变）。
• 3.选择2个第 i 个硬币，要使总和为 j，那么就要在前面 i - 1个硬币中凑到总和为j - 2*coins[i]，在前面的基础上加上两枚第 i 个硬币，所以dp[i][j] = dp[i-1][j-2*coinst[i]]。
• 4........

以上所有的情况都会出现，我们需要求上面所有情况的总和，但是遍历一遍需要O(N)的时间，我们还和前面的题目一样，将所有的情况使用一个数来代替。

所以最终dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]（注意需要判断 j - conis[i] >= 0，否则会越界）

总结

1. 状态表示：dp[i][j]表示：从前 i 个硬币中挑选，使得硬币的总和正好等于 j ，一共有多少种选法。
2. 推导状态转移方程：dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
3. 初始化：额外添加一行一列，第一行初始化为0，dp[0][0]为1。
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i][j-coins[i]]所以从上往下，从左往右填表。
5. 返回值：dp[n][amount]。

题解：

class Solution 
{
public:
    int change(int amount, vector<int>& coins) 
    {
        int n = coins.size();
        //dp[i][j]表示从前i个硬币中选，使得硬币总和为j的总方法数
        vector<vector<double>> dp(n + 1, vector<double>(amount + 1, 0));
        dp[0][0] = 1;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 0; j <= amount; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - coins[i-1] >= 0)
                    dp[i][j] += dp[i][j-coins[i-1]];
            }
        }
        return dp[n][amount];
    }
};

优化

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维即可，甚至都不需要改变遍历方向。

class Solution 
{
public:
    int change(int amount, vector<int>& coins) 
    {
        int n = coins.size();
        //dp[i][j]表示从前i个硬币中选，使得硬币总和为j的总方法数
        vector<double> dp(amount + 1, 0);
        dp[0] = 1;
        for (int i = 1; i <= n; i++)
        {
            for (int j = coins[i-1]; j <= amount; j++)
            {
                dp[j] += dp[j-coins[i-1]];
            }
        }
        return dp[amount];
    }
};

3.2.4 完全平方数

题目链接：279. 完全平方数 - 力扣（LeetCode）

这题本质上也是一个完全背包问题，每个完全平方数都是无限多个。

算法原理：

状态表示

根据完全背包的状态表示，完全背包的状态表示：dp[i][j]表示：从前 i 个物品中挑选，使得总体积不超过 j，所有的选法中最大的价值。

这题只需要在完全背包的基础上修改一下即可，dp[i][j]表示：从前 i 个完全平方数中挑选，使得总和正好等于 j，所有的选法中最少的数量。

状态转移方程

第一个数的完全平方数是1，第二个是2^2，第三个是3^2，第i个是i^2，在第i个位置时有下面几种情况。

• 1.不选择第 i 个完全平方数，那么就要在前 i - 1个完全平方数中，找到总和为 j 的，所以dp[i][j] = dp[i-1][j]。
• 2.选择1个 i^2，要使总和为j，那么就要去前i - 1个数中，找到总和为 j - i*i，所以dp[i][j] = dp[i-1][j-i*i] + 1。
• 3.选择2个 i^2，要使总和为j，那么就要去前i - 1个数中，找到总和为 j - 2*i*i，所以dp[i][j] = dp[i-1][j-2*i*i] + 2。
• 4.........

以上所有的情况都会出现，我们需要求上面所有情况的最小值，但是遍历一遍需要O(N)的时间，我们还和前面的题目一样，将第一种情况后面所有的情况使用一个数来代替。

所以最终dp[i][j] = min(dp[i-1][j], dp[i][j-i^2] + 1)。

总结

1. 状态表示：dp[i][j]表示：从前 i 个完全平方数中挑选，使得总和正好等于 j，所有的选法中最少的数量。
2. 推导状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-i*i] + 1)
3. 初始化：额外添加一行一列，dp[0][0]为0，第一行其他位置初始化为0x3f3f3f3f（为了防止出现求min时干扰数据，同时这个数也可以代表无穷大，并且比INT_MAX好的地方在于他在计算后不会发生越界）
4. 填表：因为填写dp[i][j]时，可能需要dp[i-1][j]，dp[i][j - i*i]所以从上往下，从左往右填表。
5. 返回值：dp[sqrt(n}][n]（比如说题目给的n是14，我们最多能取到小于等于n的最大的完全平方数，即9，而3的平方是9，所以i的最大取值就是3，所以在创建数组和放回结果时都是根号n。

题解：

class Solution 
{
public:
    int numSquares(int n) 
    {
        int m = sqrt(n);
        //dp[i][j]表示从前i个完全平方数中挑选，使得总和为j的最少的数量
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0x3f3f3f3f));
        dp[0][0] = 0;

        for (int i = 1; i <= m; i++)
        {
            for (int j = 0; j <= n; j++)
            {
                dp[i][j] = dp[i-1][j];
                if (j - i * i >= 0)
                    dp[i][j] = min(dp[i][j], dp[i][j-i*i] + 1);
            }
        }
        return dp[m][n];
    }
};

优化

同样这题也是可以使用滚动数组优化的，我们直接在原来的代码上进行修改，删掉一维即可，甚至都不需要改变遍历方向。

class Solution 
{
public:
    int numSquares(int n) 
    {
        int m = sqrt(n);
        //dp[i][j]表示从前i个完全平方数中挑选，使得总和为j的最少的数量
        vector<int> dp(n + 1, 0x3f3f3f3f);
        dp[0] = 0;

        for (int i = 1; i <= m; i++)
        {
            for (int j = i * i; j <= n; j++)
            {
                dp[j] = min(dp[j], dp[j-i*i] + 1);
            }
        }
        return dp[n];
    }
};

3.3 二维费用背包问题

在前面的01背包和完全背包中，限定条件往往都只有一个，比如体积限制，而二维费用的背包问题中往往会有两个限制条件，比如说体积+重量，如果不太理解的话，可以通过学习下面的例题。

3.3.1 一和零

题目链接：474. 一和零 - 力扣（LeetCode）

算法原理：

这里的限定条件是要让0的个数小于等于m，1的个数小于等于n，像这种有两个限定条件的就是二维背包问题。

每个字符只会有选和不选两种情况，所有这题是二维费用的01背包问题。

状态表示

我们先来看一下01背包的状态表示，dp[i][j]表示：从前 i 个物品中挑选，总体积不超过 j，所有的选法中最大的价值。

而二维背包就是在一维的基础上增加一维，所以二维背包的状态表示可以定义为，dp[i][j][k]表示：从前 i 个字符串中挑选，字符0的个数不超过j，字符1的个数不超过k，所有选法中最大的长度。

状态转移方程

推导状态转移方程还是根据最近的一步，即在第 i 个字符时，有以下两种情况：

• 1.不选择strs[i]，那么我们就要在前 i - 1 个字符中找到0的个数不超过j，1的个数不超过k，所以dp[i][j][k] = dp[i-1][j][k]。
• 2.选择strs[i]，假如strs[i]中0的个数为a，1的个数为b，那么要使加上strs[i]后0的总和为j，1的总和为k，我们就需要在前 i - 1 个字符中选择0的个数为j-a，1的个数为k-b的子集，所以dp[i][j][k] = dp[i-1][j-a][k-b] + 1。

上面两种情况都有可能，最终我们要求两者的最大值，所以dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-a][k-b] + 1)。

二维费用的背包问题和一维的推到方式其实是一摸一样的，只是增加了一个字符而已。

总结

1. 状态表示：dp[i][j][k]表示：从前 i 个字符串中挑选，字符0的个数不超过j，字符1的个数不超过k，所有选法中最大的长度
2. 推导状态转移方程：dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-a][k-b] + 1)。
3. 初始化：因为此时的dp表是三维了，所以需要在三个方向上都额外添加一格，防止数组越界，并将dp表全部初始化为0（如果i为0，那么无法使得0和1的数量等于j和k，所以i为0的情况都初始化为0，而j和k为0的情况可以在填表逻辑中，所以不用初始化）。
4. 填表：因为填写dp[i][j][k]时，可能需要dp[i-1][j][k]，dp[i-1][j-a][k-b]所以从上往下填表即可。
5. 返回值：dp[len][m][n]。

题解：

class Solution 
{
public:
    int findMaxForm(vector<string>& strs, int m, int n) 
    {
        int len = strs.size();
        //dp[i][j][k]表示：从前i个字符中选，使得0的个数不超过m，1的个数不超过n
        vector<vector<vector<int>>> dp(len + 1, vector(m + 1, vector<int>(n + 1)));

        for (int i = 1; i <= len; i++)
        {
            //计算strs[i-1]中0和1的个数
            int a = 0, b = 0;
            for (auto ch : strs[i-1])
            {
                if (ch == '0') ++a;
                else ++b;
            }
            
            for (int j = 0; j <= m; j++)
            {
                for (int k = 0; k <= n; k++)
                {
                    dp[i][j][k] = dp[i-1][j][k];
                    if (j - a >= 0 && k - b >= 0)
                        dp[i][j][k] = max(dp[i][j][k], dp[i-1][j-a][k-b] + 1);
                }
            }
        }       
        return dp[len][m][n];
    }
};

优化

同样这题也是可以使用滚动数组优化的，道理和一维背包问题是一样的，就是删除 i 那一维，然后改变 j 和 k 个遍历顺序（从后往前）因为填写dp[i][j][k]时，需要的两个值为dp[i-1][j][k]和dp[i-1][j-a][k-b]，如果从前往后，在填写dp[i-1][j-a][k-b]时就会将旧值覆盖掉，影响最终结果。

class Solution 
{
public:
    int findMaxForm(vector<string>& strs, int m, int n) 
    {
        int len = strs.size();
        //dp[i][j][k]表示：从前i个字符中选，使得0的个数不超过m，1的个数不超过n
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));

        for (int i = 1; i <= len; i++)
        {
            //计算strs[i-1]中0和1的个数
            int a = 0, b = 0;
            for (auto ch : strs[i-1])
            {
                if (ch == '0') ++a;
                else ++b;
            }

            for (int j = m; j >= a; j--)
            {
                for (int k = n; k >= b; k--)
                {
                    dp[j][k] = max(dp[j][k], dp[j-a][k-b] + 1);
                }
            }
        }       
        return dp[m][n];
    }
};

3.3.2 盈利计划

题目链接：879. 盈利计划 - 力扣（LeetCode）

这题的题目意思就是：有一些工作，工作的利润是profit[i]，需要group[i]个人一起参与，现在我们要选择一些任务出来，使得总人数小于等于n，总利润大于等于minProfit，一共有多少种计划。

在理解题意之后，就可以很容易知道这题是二维背包中的01背包问题（限制条件有两个：要使总人数小于等于n，总利润大于等于minProfit，每个工作只能做一次）

算法原理：

状态表示

dp[i][j][k]表示：从前 i 个工作中挑选，总人数不超过 j，总利润至少为 k，一共有多少种选法。

状态转移方程

在面临第 i 个工作时，有两种选择：

• 1.不选择第 i 个工作，那么我们就要在前 i - 1 个工作中找，使得总人数不超过j，总利润至少为k，那么dp[i][j][k] = dp[i-1][j][k]。
• 2.选择第 i 个工作，第i个工作的利润为profit[i]，需要的人数为group[i]，要使总人数不超过j，那么就要在前 i - 1 个工作中找到总人数不超过 j - group[i]（这里的j - group[i]是不能小于0的，因为j - group[i] < 0，即j < group[i]，也就是说第i个工作要的人比总人数还多，所以不行）；再来分析利润，要使总利润为至少为k，那么就要在前 i - 1个工作中找到总利润至少为 k - profit[i]（这里的k - profit[i]是可以小于0的，即 k < profit[i]，利润自然是越多越好，所以profit比k大自然更好，所以说理论上k - profit[i]可以小于0，但是作为数组下标，k - profit[i]是不能小于0的，我们可以让k - profit[i]小于0时，总利润至少为0就行）所以dp[i][j][k] = dp[i-1][j-group[i]][max(0, j-profit[i])]。

上面两种情况都存在，所以最终dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-group[i]][max(0, j-profit[i])]

 

初始化

我们需要在每个方向上额外添加一格，dp[i][j][k]其中的j表示的是总人数，k表示的是利润，如果 i 为0时，不存在任务，那么利润也就不存在，此时dp[0][j][0]中j不管取任何值都会存在一个空集，所以dp[0][j][0]初始化为1，

总结

1. 状态表示：dp[i][j][k]表示：从前 i 个工作中挑选，总人数不超过 j，总利润至少为 k，一共有多少种选法。
2. 推导状态转移方程：dp[i][j][k] = dp[i-1][j][k] + dp[i-1][j-group[i]][max(0, j-profit[i])]
3. 初始化：因为此时的dp表是三维了，所以需要在三个方向上都额外添加一格，防止数组越界，并将dp[0][j][0]初始化为1，其他位置初始化为0。
4. 填表：因为填写dp[i][j][k]时，可能需要dp[i-1][j][k]，dp[i-1][j-group[i]][k-profit[i]]所以从上往下填表即可。
5. 返回值：dp[len][n][minProtif]。

题解：

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) 
    {
        int len = group.size();
        //dp[i][j][k]表示：从前i个工作中选，使得总人数不超过j，总利润至少为j的所有选法。
        vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(n + 1, vector<int>(minProfit + 1, 0)));
        //初始化dp[0][j][0];
        for (size_t j = 0; j <= n; j++)
            dp[0][j][0] = 1;

        //填表
        for (int i = 1; i <= len; i++)
        {
            for (int j = 0; j <= n; j++)
            {
                for (int k = 0; k <= minProfit; k++)
                {
                    dp[i][j][k] = dp[i-1][j][k];
                    if (j - group[i-1] >= 0)
                    {
                        dp[i][j][k] += dp[i-1][j-group[i-1]][max(0, k - profit[i-1])];
                        dp[i][j][k] %= (1000000007);
                    }
                }
            }
        }    
        return dp[len][n][minProfit];
    }
};

优化：

同样这题也是可以使用滚动数组优化的，道理和一维背包问题是一样的，就是删除 i 那一维，然后改变 j 和 k 个遍历顺序（从后往前）因为填写dp[i][j][k]时，需要的两个值为dp[i-1][j][k]和dp[i-1][j-group[i]][k-profit[i]]，如果从前往后]就会将旧值覆盖掉，影响最终结果。

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) 
    {
        int len = group.size();
        //dp[i][j][k]表示：从前i个工作中选，使得总人数不超过j，总利润至少为j的所有选法。
        vector<vector<int>> dp(n + 1, vector<int>(minProfit + 1, 0));
        //初始化dp[0][j][0];
        for (size_t j = 0; j <= n; j++)
            dp[j][0] = 1;

        //填表
        for (int i = 1; i <= len; i++)
        {
            for (int j = n; j >= group[i-1]; j--)
            {
                for (int k = minProfit; k >= 0; k--)
                {
                    dp[j][k] += dp[j-group[i-1]][max(0, k - profit[i-1])];
                    dp[j][k] %= (1000000007);
                }
            }
        }    
        return dp[n][minProfit];
    }
};

3.4 似包非包

高中学过排列组合，其中组合是无序的，排列是有序的，比如1,1,2这三个数，在组合中算一种情况，但是排列中有三种情况，分别是1,1,2  1,2,1和2,1,1。

背包问题能够解决的一类题是：有限定条件下的组合问题。

所以在前面的背包问题中求的是组合数，不用考虑顺序，但是可能会遇到一类题：有限定条件下的排列问题，这类题是不能使用背包问题解决的。

有的题解可能会说这类问题是可以用背包问题解决的，但是大多数只是硬套背包的模板，解释起来也非常牵强，我们在平常练习一道题时，不能只是为了将题目通过，还要知道这题为什么可以这样写。

3.4.1 组合总和IV

题目链接：LCR 104. 组合总和 Ⅳ - 力扣（LeetCode）

这道题虽然名字是组合，但是示例一中就表明要求的序列要是有序的，所以这题的题目应该改成排列总和，题目中的组合其实是数学中排列的意思。

算法原理：

状态表示

这道题既然不是背包问题，我们就把他当作常规的dp题即可，我们定义状态表示的经验常常是：以某个位置为结尾..... / 以某一段区间.......

但是这题是不能使用上面的经验的，这题需要在分析问题的过程中发现重复问题，抽象出来一个状态表示。（这类状态表示也是动态规划中最难的一类）

假如说，先有[a,b,c,d]四个数，所以我们就有四个位置可以填，如果说我们把第一个位置填写为a，那么就要使剩下3个位置总和为target - a。

本来这个问题是要在整个区间中找到总和为target有多少种方法，现在就变成了，固定第一个位置，在剩下位置中找到总和为target - a有多少种方法，有了重复子问题后，我们就要开始抽象出状态表示。

dp[i]表示：凑成总和为 i ，一共有多少种排列数。

状态转移方程

我们还是根据最后一个位置来推导状态转移方程，假设最后一个位置放nums[j]，要使总和为i，那么我们就要在前面找到总和为i - nums[j]。

假如说在前面的总和为i - nums[j]一共有n种排列数，那么在每一种排列情况的后面添加nums[j]，所以之前有多少种情况，添加之后就有多少种情况。

所以dp[i] = dp[i-nums[j]]，但是nums数组中所有数都可能放在最后一个位置，所以dp[i] += dp[i-nums[i]]（注意这里 i - nums[i]要大于等于0，否则会越界）

总结

1. 状态表示：dp[i]表示：凑成总和为 i ，一共有多少种排列数。
2. 推导状态转移方程：dp[i] += dp[i-nums[i]]
3. 初始化：dp表需要额外添加一格，并将dp[0]设置为1
4. 填表：从左向右填表。
5. 返回值：dp[target]。

题解：

class Solution 
{
public:
    int combinationSum4(vector<int>& nums, int target) 
    {
        int n = nums.size();
        //dp[i]表示总和为i的所有排列数
        vector<double> dp(target + 1, 0);
        dp[0] = 1;

        for (int i = 1; i <= target; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (i - nums[j] >= 0)
                    dp[i] += dp[i - nums[j]];
            }
        }
        return dp[target];
    }
};

4.卡特兰数

4.1 不同的二叉搜索树

题目链接：96. 不同的二叉搜索树 - 力扣（LeetCode）

算法原理：

状态表示

这题和上道题一样，直接定义状态表示不太好定义，那么我们就要在分析问题的过程中，发现重复子问题，然后抽象出一个状态表示。

假设一共有五个结点分别为1,2,3,4,5，如果根节点的位置放3号结点，那么根据搜索树的定义，我们就可以确定根节点左边只有两个结点，根节点右边也只有两个结点，那么这个问题就转化成了，两个结点有多少个二叉搜索树。

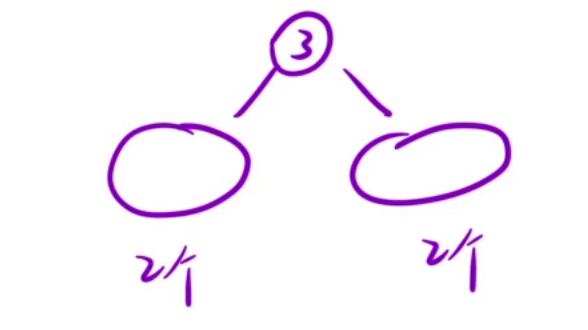
那么我们就可以将dp[i]表示为：结点个数为 i 时，一共有多少种二叉搜索树。

状态转移方程

当结点个数为 i 时，假如说我们任选一个 j 作为根节点，那么根节点的左子树应该有 j - 1个结点，右子树应该有 i - j 个，左边的j - 1个结点一共有dp[j-1]种二叉搜索树，右边的i - j一共有dp[i-j]种二叉搜索树，那么dp[i][j] = dp[j-1] * dp[i-j]。

而 j 在[1, i]范围内都可以作为根节点，所以最终dp[i][j] += dp[j-1] * dp[i-j]。（这个公式就是卡特兰数）

总结

1. 状态表示：dp[i]表示为：结点个数为 i 时，一共有多少种二叉搜索树。
2. 推导状态转移方程：dp[i][j] += dp[j-1] * dp[i-j]
3. 初始化：dp表需要额外添加一格，并将dp[0]设置为1
4. 填表：从左向右填表。
5. 返回值：dp[n]。

class Solution 
{
public:
    int numTrees(int n) 
    {
        //dp[i]表示：i个数一共有多少种二叉搜索树
        vector<int> dp(n + 1, 0);
        dp[0] = 1;

        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= i; j++)
            {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
};