acWing 123. 士兵

原创已于 2023-10-24 17:28:54 修改 · 95 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#1024程序员节

于 2023-10-24 17:27:31 首次发布

acwing算法竞赛进阶指南专栏收录该内容

7 篇文章

订阅专栏

文章讲述了如何解决士兵问题中的X坐标统一问题，通过排序和利用中位数概念，将其转化为货仓选址问题。作者提供了详细的步骤和代码示例，展示了如何通过计算绝对差值来找到最小答案。

传送门：123. 士兵 - AcWing题库

对于y的话，就是取中位数，x则需要先排序，详情见（104. 货仓选址 - AcWing题库）

士兵的最终X坐标显然是不一样的，怎么办呢？很简单，只要把他们的X
统一就行了，把x[i]每个都减i（这个操作的前面要排序，才可使答案最小）。又变成货仓选址了。

对于x的操作理解如下：

x首先要排序，排序后的先后位次就是最后的位次
具体可按照图片，分多钟情况画一下就会知道了。

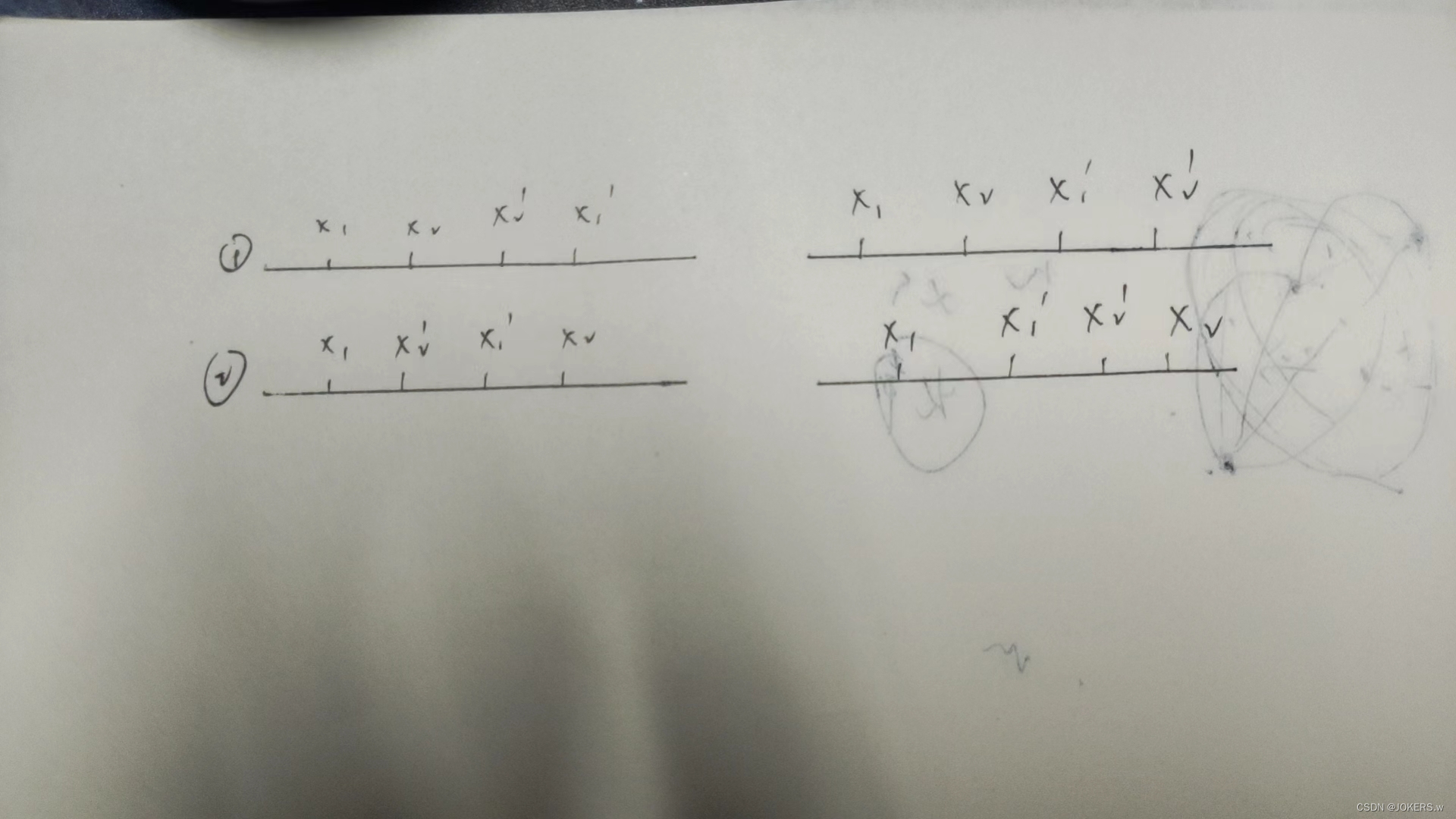
第一次排序之后，假设最后放置好的位置的最左边是d+1，那么他们依次为的位置d+1，d+2,......,d+n;
那么题目要求的是
|x[1]-(d+1)| + |x[2]-(d+2)| + ...... + |x[n]-(d+n)|的最小值
也就是求
|(x[1]-1)-d| + |(x[1]-2)-d| + ...... + |(x[n]-n)-d|的最小值
这样看的话应该就明白了吧（这个表述就跟货仓选址一样了），如果不明白，就去看看货仓选址。
注：
（取中位数的原因可以做做另一道题：104. 货仓选址 - AcWing题库此处贴出蓝书对其（货仓选址）关于选取中位数的证明：把A[1]~A[N] 排序，设货仓建在 X 坐标处，X 左侧的商店有P家，右侧的商店有Q家。若 P小于Q，则每把货仓的选址向右移动1单位距离，距离之和就会变小 Q-P。同理，若 P大于Q，则货仓的选址向左移动会使距离之和变小。当 P=Q 时为最优解。）

代码：

#define _CRT_SECURE_NO_WARNINGS
//#pragma GCC optimize(1)
//#pragma GCC optimize(2)
//#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
#define N 5000005 
#define M 1331 
#define PII pair<int,int>
#define PIII pair<pair<int,int>,int>  
#define VPII vector<PII>
#define VPIII vector<PIII>
#define inf 0x3f3f3f3f3f3f  
#define ll long long
#define ull unsigned long long
const double eps = 1e-6;
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define mod 1000000007
ll a[N],x[N],y[N];
ll n,m;
void solve() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> x[i]>>y[i];
	}
	sort(y + 1, y + 1 + n);
	sort(x + 1, x + 1 + n);
	for (int i = 1; i <= n; i++) {
        	x[i]-=i;
	}
		sort(x + 1, x + 1 + n);
	m = n / 2;
	if (n & 1) m++;
	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ans += abs(y[m] - y[i]);
		ans += abs(x[m] - x[i]);
	}
	cout << ans << "\n";
}
int main()
{
	IOS;
	solve();
	return 0;
}