[洛谷-P3698][CQOI2017]小Q的棋盘

一、问题

题目描述

小 Q 正在设计一种棋类游戏。

在小 Q 设计的游戏中，棋子可以放在棋盘上的格点中。某些格点之间有连线，棋子只能在有连线的格点之间移动。整个棋盘上共有 $V$ 个格点，编号为 $0,1,2,\cdots ,V-1$，它们是连通的，也就是说棋子从任意格点出发，总能到达所有的格点。小 Q 在设计棋盘时，还保证棋子从一个格点移动到另外任一格点的路径是唯一的。

小 Q 现在想知道，当棋子从格点 $0$ 出发，移动 $N$ 步最多能经过多少格点。格点可以重复经过多次，但不重复计数。

输入格式

第一行包含2个正整数 $V,N$，其中 $V$ 表示格点总数，$N$ 表示移动步数。

接下来 $V-1$ 行，每行两个数 $a_i,b_i$，表示编号为$a_i,b_i$ 的两个格点之间有连线。

输出格式

输出一行一个整数，表示最多经过的格点数量。

样例 #1

样例输入 #1

5 2
1 0
2 1
3 2
4 3

样例输出 #1

3

样例 #2

样例输入 #2

9 5
0 1
0 2
2 6
4 2
8 1
1 3
3 7
3 5

样例输出 #2

5

提示

【输入输出样例 1 说明】

从格点 $0$ 出发移动 $2$ 步。经过 $0,1,2$ 这 $3$ 个格点。

【输入输出样例 2 说明】

一种可行的移动路径为 $0\to 1\to 3\to 5\to 3\to 7$，经过 $0,1,3,5,7$ 这 $5$ 个格点。

【数据规模与约定】

对于 $100\%$ 的测试点，$1\le N,V\le 100$，$0\le a_i,b_i<V$。

二、分析

这道题的意思就是：我从树中的某个点开始走，在$N$步之内所能经过的最多的节点。其中，这些点是可以反复经过的。也就是说，我走到某个子节点的时候，可以回头走。

而这道题的难点也在于可以回头。

1、状态表示

$f[u][k][0]$表示从$u$节点出发，走不超过$k$步，并且最终回到$u$点的情况下，所能经过的最大的节点数。
$f[u][k][1]$表示从$u$节点出发，走不超过$k$步，并且最终没有回到$u$点的情况下，所能经过的最大的节点数。

2、状态转移

第一种情况就是我们回到了$u$点。这种情况下，我们如何写转移方程呢？

我们这里采用的书写方式还是按照树形背包DP的模板来写的，即针对当前子树进行讨论。
我们看下面的图：

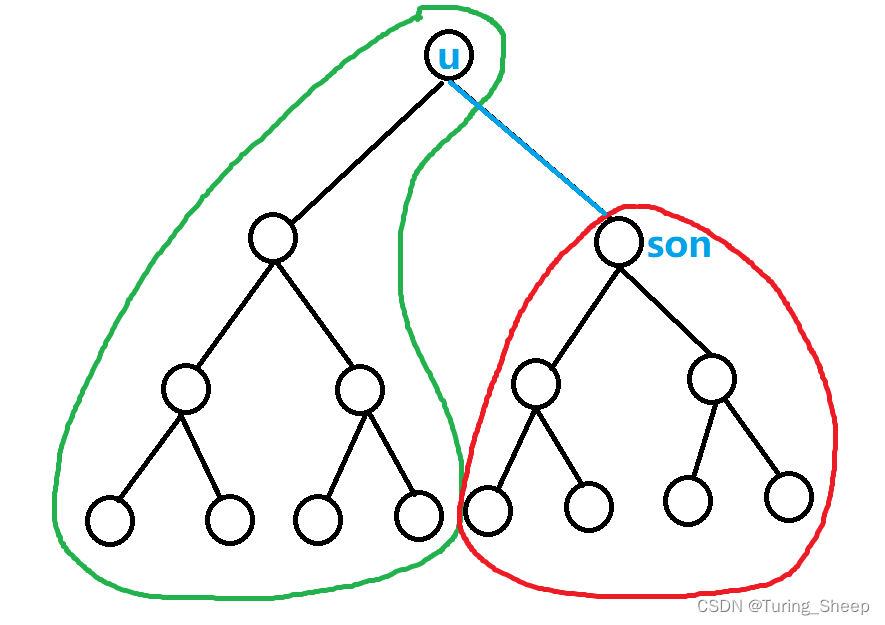
我们从$u$出发，先深入到绿色的区域中，再回到$u$点，然后从$u$点深入到红色区域中，再从红色区域中回到$son$，再从$son$回到$u$。那么这个过程可以写成下面的形式。

$$f[u][k][0]=max(f[u][k][0],f[u][k-j][0]+f[son][j-2][0])$$
这里减去2是因为图中的蓝色线被我们走了两次。所以我们留给红色区域内部的点的步数只有$j-2$步。

另外一种情况就是我们不会回到$u$点，在这种情况下，我们最终停留的位置有三种可能，第一种就是留在绿色的区域。我们先进入红色区域，再回到$son$，再从$son$回到$u$，再从$u$到绿色的区域。
该过程可以写作下面的代码：
$$f[u][k][1]=max(f[u][k][1],f[u][k-j][1]+f[son][j-2][0])$$
另外就是我们可以先走绿色区域，然后回到$u$点，接着我们深入红色区域，到了红色区域，我们还分为两种情况，第一种情况是停留在$son$点上，另外一种是停留在除了$son$之外的红色区域内的点上。由于我们只经过了一次蓝色的边，所以不需要减去2，只需要减去1。
$$f[u][k][1]=max(f[u][k][1],f[u][k-j][0]+max(f[son][j-1][1],f[son][j-1][0]\left)\right)$$

3、初始化

我们最差的情况下，也是经过1个点（本身），所以我们需要将其初始化为1。

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e2 + 10;
vector<int>edge[N];
ll f[N][N][2];
int n, k;
/*
f[u][j][0] ==> 从u点出发，在不超过k步的情况下，并且最终回到U点，所能经过最多的点
f[u][j][1] ==> 从u点出发，在不超过k步的条件下，并且最终不会到u点，所能经过的最多的点。

*/
void dp(int u, int father)
{
	for(int i = 0; i <= k; i ++ )
		f[u][i][0] = f[u][i][1] = 1;

	for(int i = 0; i < edge[u].size(); i ++ )
	{
		int son = edge[u][i];
		if(son == father)
			continue;
		dp(son, u);
		for(int j = k; j >= 0; j -- )
		{
			for(int q = 0; q <= j; q ++ )
			{
				if(q >= 2)
					f[u][j][0] = max(f[u][j][0], f[u][j - q][0] + f[son][q - 2][0]);
				
				if(q >= 1)
					f[u][j][1] = max(f[u][j][1], f[u][j - q][0] + max(f[son][q - 1][1], f[son][q - 1][0]));
				
				if(q >= 2)
					f[u][j][1] = max(f[u][j][1], f[u][j - q][1] + f[son][q - 2][0]); 

			}
		}
	}
}

void solve()
{
	cin >> n >> k;

	for(int i = 0; i < n - 1; i ++ )
	{
		int a, b;
		cin >> a >> b;
		edge[a].push_back(b);
		edge[b].push_back(a);
	}

	dp(0, -1);

	cout << max(f[0][k][0], f[0][k][1]) << endl;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	solve();
}