手把手拆解三大复杂排序算法（快速排序）

嗨，大家好，我是心海，这是我的算法篇，第四篇文章！

目录

一、算法介绍

二、算法原理与实现

三、时空复杂度分析

四、测试对比

五、总结

---

一、算法介绍

快速排序算法的核心思想是“分而治之”，它通过不断地将待排序序列划分成较小的子序列，然后分别对这些子序列进行排序，最终将整个序列有序化。它是由 C.A.R.Hoare 在 1962 年提出的，以其高效性而闻名，尤其在处理大规模数据时表现优异，是很多实际应用场景中的首选排序算法。

二、算法原理与实现

快速排序相对于前面基础排序算法（冒泡排序、插入排序、选择排序）会稍微复杂一点点

可以分为三个步骤

1. 选基准 ：挑一个元素作为基准值（pivot），一般是第一个元素，也可以最后一个元素、中间的元素或者随机选一个。

2. 分区 ：把序列中小于基准值的元素放在基准值左边，大于基准值的元素放在右边，这一步骤完成后，基准值就处于它在有序序列中的最终正确位置。

3. 递归排序 ：对基准值左边和右边的子序列分别重复上述步骤，直到子序列长度为 1（也就是整个序列已经有序）。

在实际操作过程中，我们会定义两个“指针”变量，首先用一个变量 tmp 取出我们的基准值，然后用left 和 right 两个变量分别指向数组两端，如下图

为了方便理解，我们可以把基准值的位置想象成空位

然后，接下来就很简单了，我们就是不断地移动元素去补充空位，同时把 left 和 right 分别向中间移动，直到二者重合

那么，怎么选择补充空位的值呢？

首先，此时 left 指向空，那么我们就看另一个指针变量 right ，看看其指向的数字是放在 tmp 右边还是左边，如果 right 指向的值大于 tmp ，则不用移动该值，而是将 right 这个指针向左移动一位，直到这个值比 tmp 小

 那么，我们就把 right 指向的值，移动到此时的空位，也就是 left 指向的位置

那么此时，right 指向空值了，那我们就移动 left ，而 left 碰到如果比 tmp 小，则执行交换

以此类推，直到最后，left 和 right 最后重合，

 最后，剩下的这个空位，就是留给我们 tmp 的

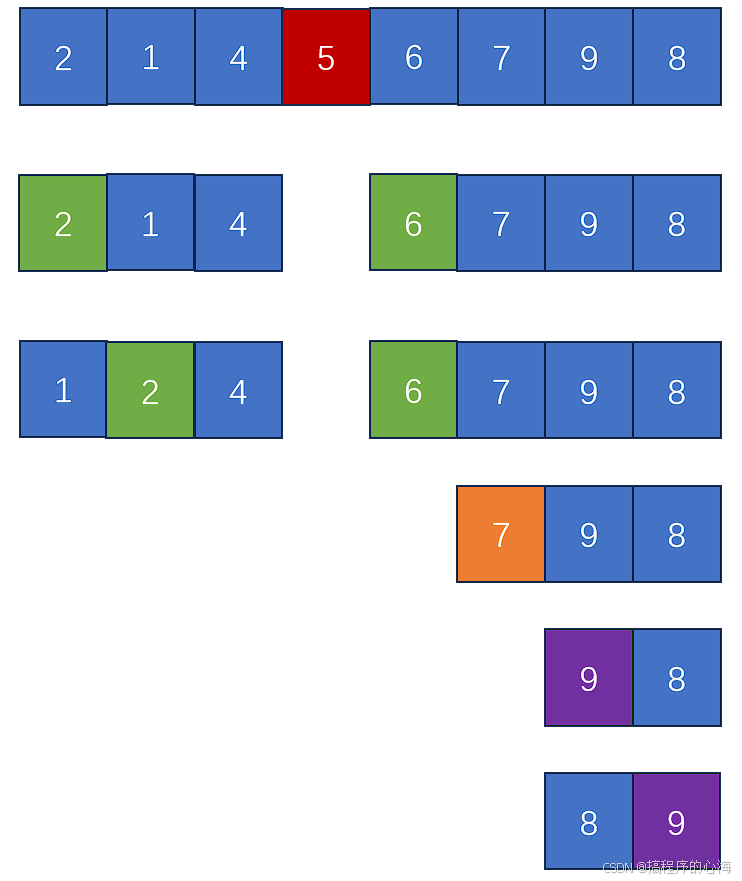
这个基准值，会把数组分为左右两部分，接下来，就是在左右的小区域不断重复递归，直到最后完成整个排序

来看代码，假设我们已经有一个函数帮我们完成前面讲解的一轮排序，那么我们就只需要递归调用

def quick_sort(li,left,right):#li是待排序数组
    if left<right:
        #至少有两个元素
        mid=partition(li,left,right)
        quick_sort(li,left,mid-1)
        quick_sort(li,mid+1,right)

上面的代码，首先当数组至少有两个元素，我们才需要排序，然后假设 partition 函数会帮我们完成一轮分区，并且返回基准值下标，也就是前面示例 tmp 的下标，然后后面分别将 tmp 左右两边的子数组传递到快速排序，也就是递归，直到完成排序即可。

那么剩下的，我们就是要完成分区工作，也就是找到基准值插入的位置、以及左右分区的工作

def partition(li,left,right):
    tmp=li[left]
    while left<right:
        while left<right and li[right]>=tmp:#从右边开始，若大于初始值则继续向前
            right-=1
        li[left]=li[right]#将右边的值补到左边空位
        while left<right and li[left]<=tmp:#接着左边开始向后检查，若小于目标值则继续
            left+=1
        li[right]=li[left]#将左边值给右边
    li[left]=tmp#最后重合，左边指针即空位
    return left

相信看完一开始的图文分析，对照这个代码应该是比较清晰了

这里解释一下，为什么两层while里面都有 left < right 这个条件？

外层的比较简单，就是意味着两个指针还没有相遇，分区未完成；

而内层如果没有这个条件，那么可能 right 会移动到索引越界，造成错误，

三、时空复杂度分析

时间复杂度

最优情况 ：每次选择的基准值都能将序列均分成两部分，此时递归树的深度为 log₂n，每一层的比较操作总共需要 O(n) 时间（每一层本质一个partition只有一个循环），所以总时间复杂度为 O(nlog₂n)，也可以简记为 O(nlogn) 。

这里补充一下，出现循环减半（问题规模折半）才会出现 O(logn) 这种时间复杂度

最坏情况 ：每次选择的基准值都是序列中的最小或最大元素，导致每次划分都只能得到一个空子序列和一个长度为 n - 1 的子序列，此时递归树的深度为 n，总时间复杂度为 O(n²)。

平均情况 ：时间复杂度为 O(nlogn)。因为快速排序在实际中对于各种类型的序列都能表现良好，且平均情况更接近最优情况。

空间复杂度

快速排序的空间主要消耗在递归调用的栈空间上。在最优情况下，递归栈的深度为 log₂n，所以空间复杂度为 O(log₂n)。在最坏情况下，递归栈的深度为 n，空间复杂度为 O(n)。

四、测试对比

为了更直观地看出快速排序的速度，我们可以简单做一下测试

随机生成一万个数字来测试一下

根据二者时间复杂度可以得出，当数据量大到一定规模时，快速排序会比冒泡排序快特别多

快速排序具有更优的时间复杂度（O(n log n)），使其在处理大规模数据时比冒泡排序（O(n²)）更有效率

五、总结

快速排序算法凭借其优雅的思路和高效的性能，在排序算法领域占据着举足轻重的地位。

它的分治思想和分区操作让人拍案叫绝，通过不断地划分和递归排序，能快速地将无序序列转换为有序序列。

不过，它也有着潜在的不足，比如在最坏情况下可能会退化成 O(n²) 的时间复杂度，以及需要用到额外的栈空间和辅助存储空间。

但在大多数实际应用场景中，快速排序仍然是一个非常优秀的排序算法，广泛应用于各种需要对数据进行快速有序排列的场景。

如果这篇文章对您有所启发，希望您能点赞关注支持一下。