LeetCode热题100：Java双指针中等难度题目精解

11. 盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例

示例 1:

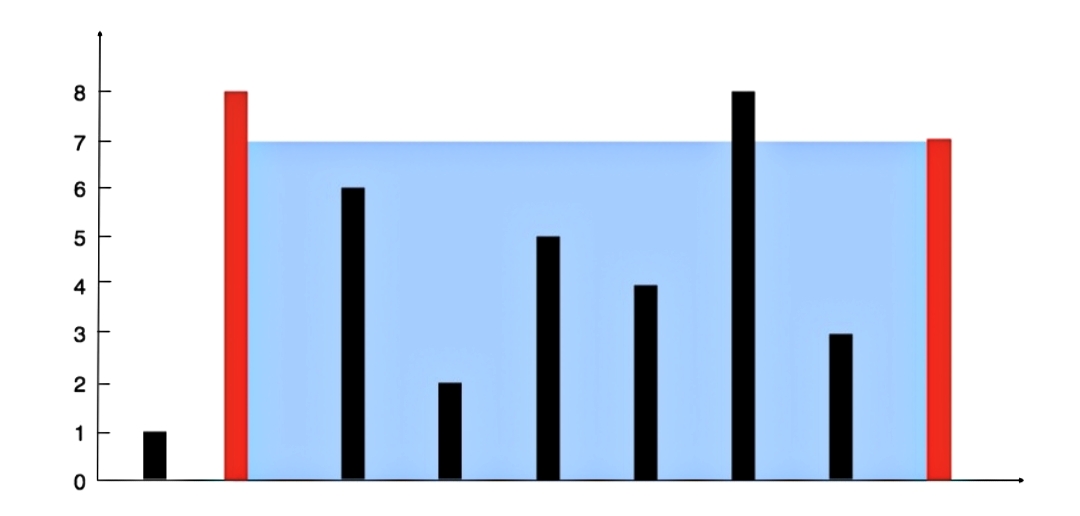
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2:

输入：height = [1,1]
输出：1

提示

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

题解

public class Solution {
    public int maxArea(int[] height) {
        // 初始化双指针，l指向数组开头，r指向数组末尾
        int l = 0, r = height.length - 1;
        // 初始化最大面积为0
        int ans = 0;
        // 当左指针小于右指针时循环
        while (l < r) {
            // 计算当前容器的面积，取较短边的高度乘以宽度
            int area = Math.min(height[l], height[r]) * (r - l);
            // 更新最大面积
            ans = Math.max(ans, area);
            // 移动较短边的指针，因为移动较长边的指针不会增加面积
            if (height[l] <= height[r]) {
                ++l; // 左指针右移
            }
            else {
                --r; // 右指针左移
            }
        }
        // 返回最大面积
        return ans;
    }
}

解题思路

1. 初始化指针：使用两个指针 l 和 r，分别指向数组的开头和末尾。这样可以计算初始的最大宽度。

2. 计算当前面积：在每次循环中，计算当前两个指针所指向的线形成的容器的面积。面积的计算公式是：min(height[l], height[r]) * (r - l)，即较短边的高度乘以宽度。

3. 更新最大面积：比较当前面积与已知的最大面积 ans，并更新 ans 为较大值。

4. 移动指针：比较 height[l] 和 height[r]，移动较短边的指针。这样做的原因是，移动较长边的指针不会增加容器的面积（因为高度受限于较短边），而移动较短边的指针有可能找到更高的边，从而可能增加面积。

5. 终止条件：当 l 和 r 相遇时，循环结束，此时已经检查了所有可能的容器组合。

15. 三数之和

问题描述

给定一个整数数组 nums，找出所有满足以下条件的三元组 [nums[i], nums[j], nums[k]]：

1. i != j, i != k, 且 j != k
2. nums[i] + nums[j] + nums[k] == 0
3. 结果中不能包含重复的三元组

示例

示例1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例2：

输入：nums = [0,1,1]
输出：[]

示例3：

输入：nums = [0,0,0]
输出：[[0,0,0]]

提示

• 3 <= nums.length <= 3000
• -105 <= nums[i] <= 105

题解

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;  // 获取数组长度
        Arrays.sort(nums);  // 对数组进行排序，这是双指针法的基础
        List<List<Integer>> ans = new ArrayList<List<Integer>>();  // 创建结果列表
        
        // 枚举第一个数a（外层循环）
        for (int first = 0; first < n; ++first) {
            // 跳过重复的a值，避免重复解
            // 注意：first > 0 确保不是第一个元素时才检查前一个
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            
            // 初始化第三个数的指针，指向数组末尾
            int third = n - 1;
            // 计算剩余两数需要满足的和（即 -a）
            int target = -nums[first];
            
            // 枚举第二个数b（内层循环）
            for (int second = first + 1; second < n; ++second) {
                // 跳过重复的b值，避免重复解
                // second > first + 1 确保不是第一个b时才检查前一个
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                
                // 移动第三个数的指针，直到找到满足条件的c或者指针相遇
                // 条件：b + c > target（即 a + b + c > 0）
                while (second < third && nums[second] + nums[third] > target) {
                    --third;  // 向左移动c指针，减小总和
                }
                
                // 如果指针重合，说明没有满足条件的c了，可以结束当前循环
                if (second == third) {
                    break;
                }
                
                // 检查是否找到满足条件的组合
                if (nums[second] + nums[third] == target) {
                    // 创建一个新的三元组列表
                    List<Integer> list = new ArrayList<Integer>();
                    list.add(nums[first]);  // 添加a
                    list.add(nums[second]); // 添加b
                    list.add(nums[third]);  // 添加c
                    ans.add(list);  // 将找到的三元组加入结果集
                }
            }
        }
        return ans;  // 返回所有找到的三元组
    }
}

解题思路

1. 数组排序

   • 首先对数组进行升序排序，这是后续双指针法的基础
   • 排序时间复杂度：O(n log n)

2. 外层循环固定第一个数

   • 遍历数组，将当前元素作为三元组的第一个数 nums[i]
   • 范围：从第一个元素到倒数第三个元素（i < n-2）

3. 跳过重复的第一个数

   • 检查当前数是否与前一个数相同
   • 若相同则跳过，避免重复解
   • 条件：i > 0 && nums[i] == nums[i-1]

4. 初始化双指针

   • 左指针 left = i + 1
   • 右指针 right = nums.length - 1
   • 目标：找到 nums[left] + nums[right] == -nums[i]

5. 双指针查找过程

   • 计算当前三数之和 sum = nums[i] + nums[left] + nums[right]
   • 三种情况处理：
     a. sum == 0：找到有效解
     b. sum < 0：需要增大和，左指针右移
     c. sum > 0：需要减小和，右指针左移

6. 处理找到解的情况

   • 将有效解加入结果列表
   • 跳过所有重复的nums[left]和nums[right]
   • 同时移动左右指针继续查找

7. 提前终止条件

   • 当nums[i] > 0时可以直接终止循环
   • 因为数组已排序，后面的数都为正数，不可能和为0