算法练习 Day17 | leetcode 110.平衡二叉树，257. 二叉树的所有路径，404.左叶子之和

一、算法题

110.平衡二叉树

题目链接

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }
        int res=blance(root);
        if(res==-1){
            return false;
        }
        return true;
    }

    public int blance(TreeNode root){
        if(root==null){
            return 0;
        }
        int left=blance(root.left);
        if(left==-1){
            return -1;
        }
        int right=blance(root.right);
        if(right==-1){
            return -1;
        }
        int len=Math.abs(left-right);
        if(len>1){
            return -1;
        }
        //计算高度
        return Math.max(left, right)+1;

    }
}

注意：

• 如果只有这个

if(len>1){
  return -1;
}

• 这个判断只会返回高度的计算结果，与下面return Math.max(left, right)+1效果是一样的，想要达到一旦不平衡就返回-1然后退出递归的效果，需要在计算left和right的时候，在他们后面加一个判断语句，一旦left或者right==-1时，就返回-1

 

 257. 二叉树的所有路径

题目链接

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res=new ArrayList<>();
        if(root==null){
            return res;
        }
        dfs(root,"",res);
        return res;
    }
    public void dfs(TreeNode root,String path,List<String>res){
        if(root==null){
            return;
        }
        //使用前序遍历的方法
        if(root.left==null&&root.right==null){
            //最后一个节点，不用往后面加箭头了
            res.add(path+root.val);
        }
        //然后处理左右子节点
        //没找到叶子节点就把这个节点的值先加进去，作为一条路径中的其中一个值，然后再在后面加箭头
        dfs(root.left, path+root.val+"->", res);
        dfs(root.right, path+root.val+"->", res);
    }
}

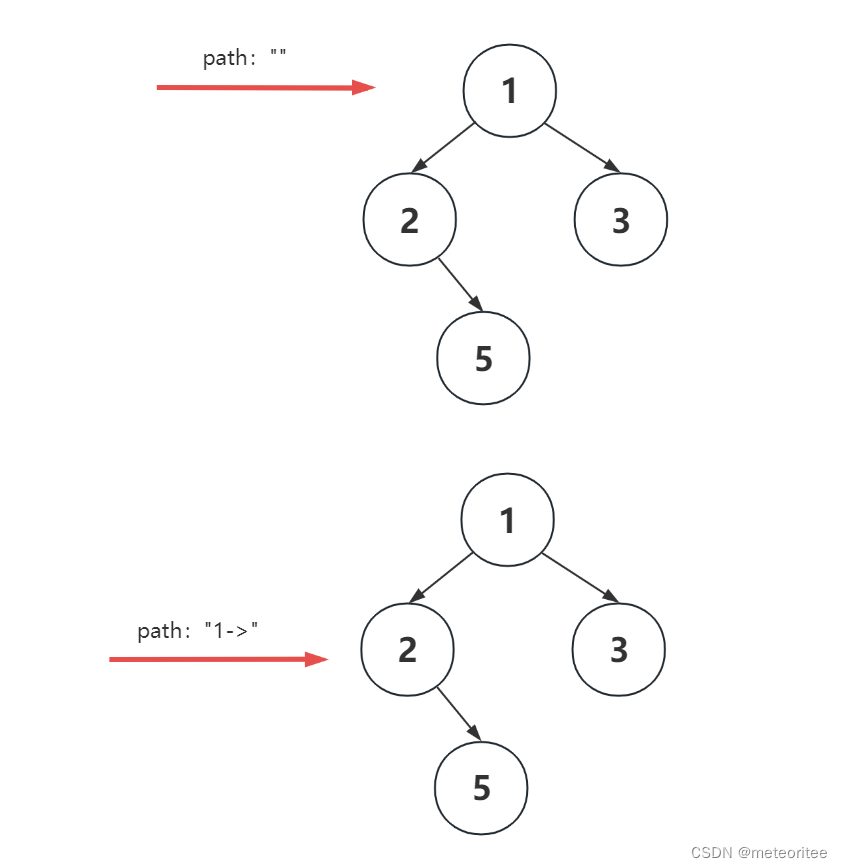
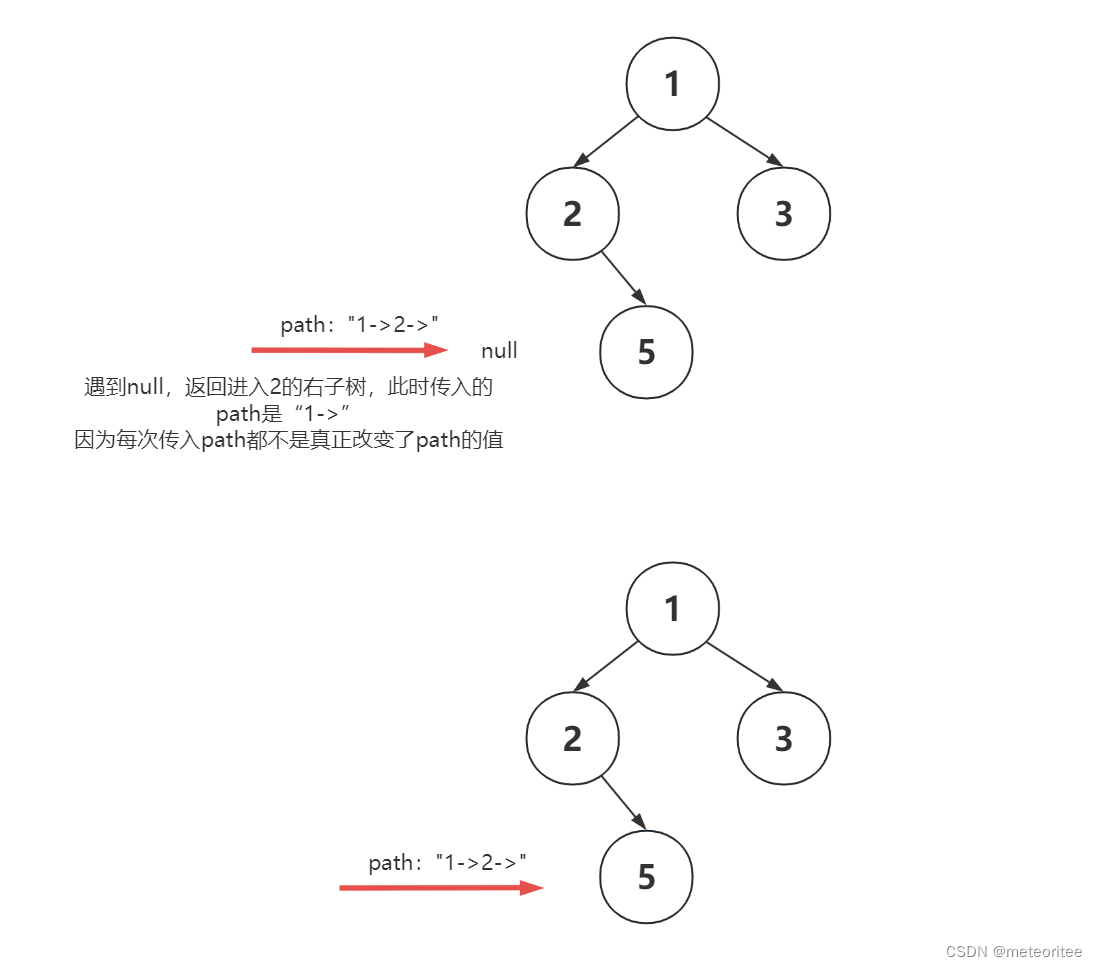
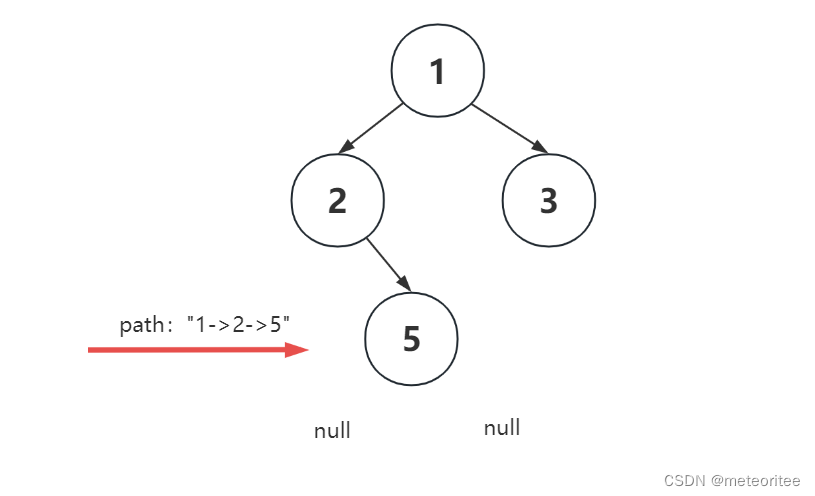
• path在里面起着一个获得路径的过程
• 每次调用dfs时，传入的参数是path+root.val+"->"，这实际上并没有改变path的值，改变的只是每次调用函数传入的值

404.左叶子之和

题目链接

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        //后序遍历
        if(root==null){
            return 0;
        }
        return sumof(root);
    }

    public int sumof(TreeNode root){
        if(root==null){
            return 0;
        }
        int left=sumof(root.left);
        int right=sumof(root.right);
        int value=0;
        if(root.left!=null&& root.left.left==null&&root.left.right==null){
            value=root.left.val;
        }
        int sum=left+right+value;
        return sum;
    }
}

• 无法用自身去判断是否是左叶子节点，因为即使是叶子节点也无法通过自己判断是不是左边的叶子节点，所以只能通过父节点来判断

• int value=0不能用int sum=0替代，因为这样就算拿到了一个左叶子节点的值，它也会在计算下一次的左叶子之和时，执行int sum=0语句，导致计算不了左叶子的和而是重复清零的情况