算法练习 Day1 | leetcode704二分查找 27移除元素

一、 基础知识

1.数组知识

• 数组内存空间的地址是连续的
• 数组的元素是不能删除的，只能覆盖

2.二分法知识

（1）二分法概念

• 二分法也叫二分查找

（2）二分法的使用前提

• 有序
• 元素唯一，无重复元素

3.快慢指针

• 快慢指针从同一侧遍历数组，两个指针以不同的策略移动，直到满足条件为止
• 本题中：
  • 快指针：无论什么情况都会向前移动，去寻找新数组里的元素（即除了应移除元素以外的所有元素）
  • 慢指针：只有满足找到新数组里的元素的条件才会向前移动，指向新数组下标

二、算法题

704. 二分查找

方法一：左闭右闭 

class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        while(left<=right){
            //middle是下标
            int middle=(left+right)/2;
            if(nums[middle]<target){
                //说明target在middle右边部分
                //即要更新左边界
                //使用的是“左闭右闭”的区间方式
                //nums[middle]<target说明已经判断出右边界小于、不会等于target
                //所以left=middle+1
                left=middle+1;
            }
            else if(nums[middle]>target){
                //说明target在middle左边部分
                //即要更新右边界
                right=middle-1;
            }
            else if(nums[middle]==target){
                return middle;
            }
        }
        //如果在左右边界一步步缩小一直到重合都没找到traget
        //说明nums数组中不存在目标值target
        return -1;

    }
}

方法二：左闭右开

class Solution {
    public int search(int[] nums, int target) {
        int left=0;
        int right=nums.length;
        //这里不能是left<=right，因为是左开右闭
        while(left<right){
            int middle=(left+right)/2;
            if(nums[middle]<target){
                //说明target在nums[middle]右边
                //修改左边界
                left=middle+1;
            }
            else if(nums[middle]>target){
                //修改右边界
                right=middle;
            }
            else if(nums[middle]==target){
                return middle;
            }
        }
        return -1;

    }
}

---

27. 移除元素

方法一：暴力求解

class Solution {
    public int removeElement(int[] nums, int val) {
        //暴力求解
        int size=nums.length;
        for(int i=0;i<size;i++){
            if(nums[i]==val){
                for(int j=i;j<size-1;j++){
                    nums[j]=nums[j+1];
                }
                size--;
                i--;
            }
        }
        return size;

    }
}

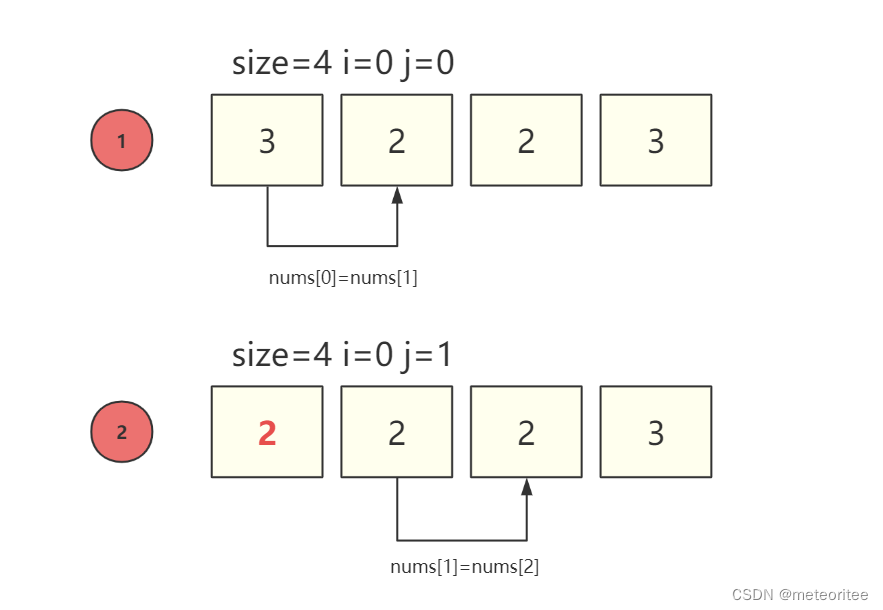
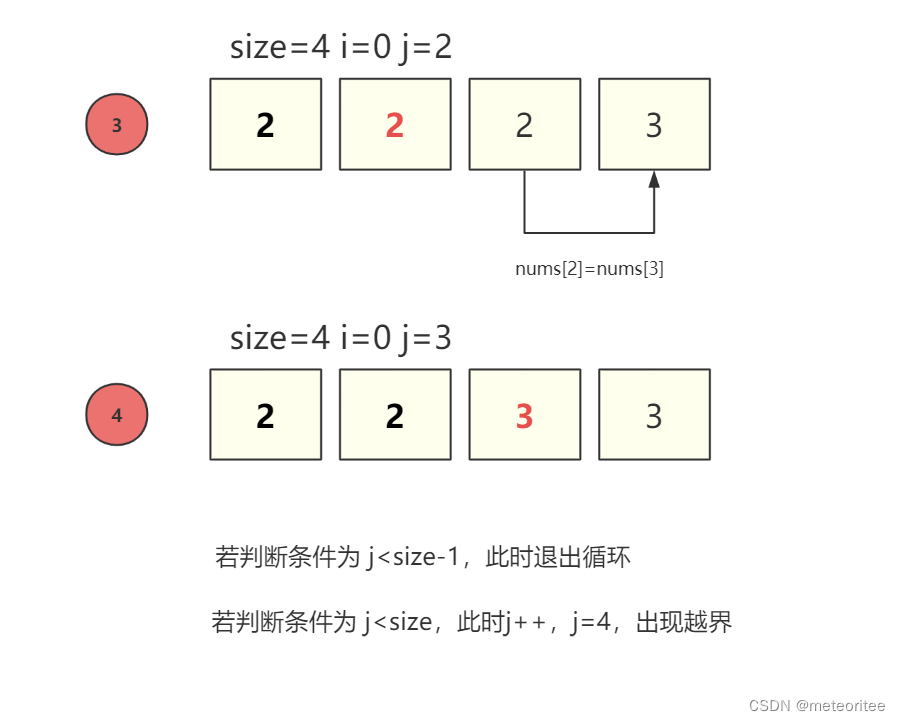
注意 ：

• 里层循环的循环终止条件应该是 j<size-1而不是 j<size
• 如果用 j<size 会导致越界问题

 

方法二：双指针法（快慢指针）

class Solution {
    public int removeElement(int[] nums, int val) {
        //快慢指针
        //快指针：无论什么情况都会向前移动，去寻找新数组里的元素（即除了应移除元素以外的所有元素）
        //慢指针：只有满足找到新数组里的元素的条件才会向前移动，指向新数组下标
        int fast=0;
        int slow=0;
        for(int i=0;i<nums.length;i++){
            if(nums[fast]!=val){
                nums[slow]=nums[fast];
                slow++;
            }
            fast++;
        }
        return slow;

    }
}

最后返回的新数组长度

• 每次循环if判断结束后，慢指针都会向前移动
• 所以最后一次循环结束后慢指针不是指向新数组最后一个元素的位置
• 而是指向新数组最后一个元素的后一个的位置
• 此时刚好慢指针指向的下标就是新数组长度