代码随想录算法训练营第十六天|104.二叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数

104.二叉树的最大深度

参考资料（代码随想录）

题目

力扣题目链接

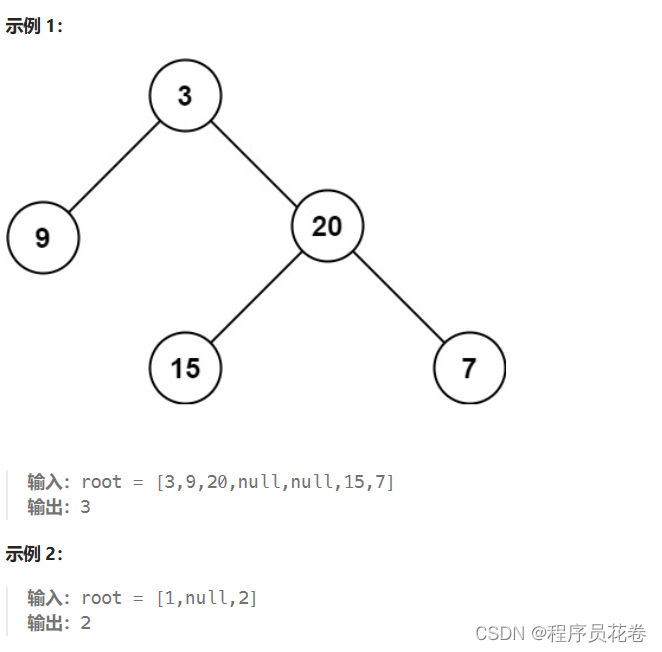
给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

思路

递归法

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

用后序遍历（左右中）来计算树的高度

1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回值是树的深度。
2. 确定终止条件：如果为空节点的话，就返回0，表示高度为0
3. 确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

代码如下（JavaScript）

var maxDepth = function(root) {
    //使用递归的方法  递归三部曲
    //1.确定递归函数的参数和返回值
    const getDepth=function(node){
      //2.确定终止条件
      if(node===null)return 0
      //3.确定单层逻辑
      let leftDepth =getDepth(node.left)
      let rightDepth=getDepth(node.right)
      let depth =1+Math.max(leftDepth,rightDepth)
      return depth
    }
    return getDepth(root)
};

 

 111.二叉树的最小深度

参考资料（代码随想录）

题目

力扣题目链接

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

 思路

这道题直觉上好像和求最大深度差不多，其实还是差不少的。

本题依然是前序遍历和后序遍历都可以，前序求的是深度，后序求的是高度。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。

以下讲解中，遍历顺序依然采用后序遍历

本题还有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：

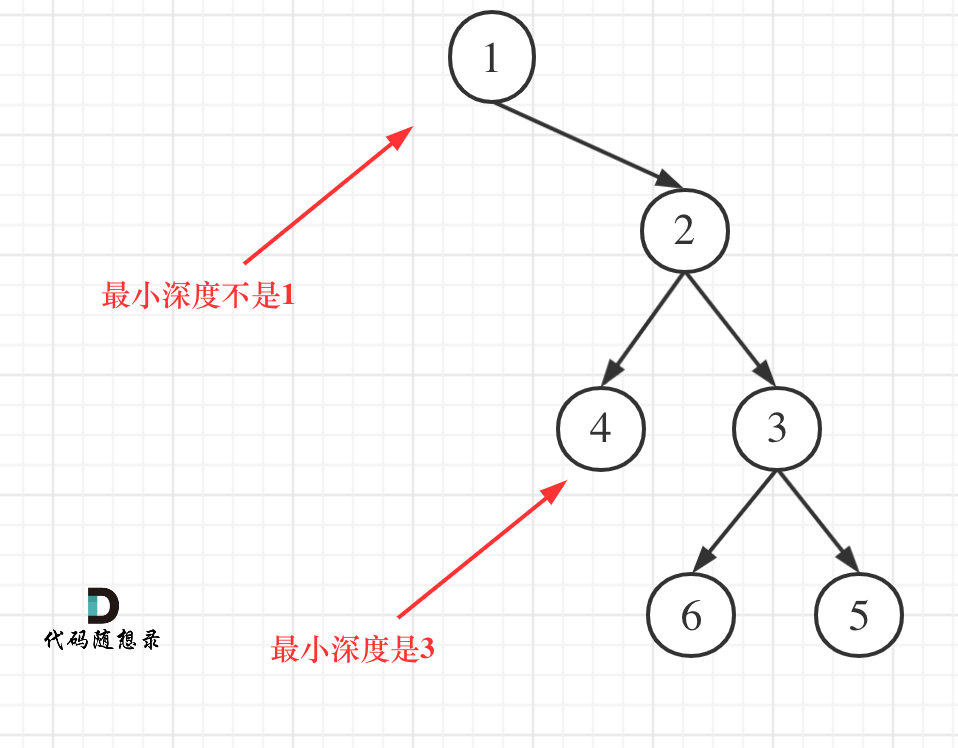
这就重新审题了，题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。，注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点！

递归法 

1. 确定递归函数的参数和返回值：参数是二叉树根节点，返回值是数值
2. 确定终止条件：遇到空节点返回0，表示高度为0
3. 确定递归单层逻辑：（注意与求最大深度的区别） 

• 如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。
• 反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。
• 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

代码如下（JavaScript）

var minDepth = function (root) {
  //递归函数  
  //1.确定函数的参数和返回值
  const getDepth = function (node) {
    //2.确定终止条件
    if (node === null) return 0
    //3.确定单层逻辑
    let leftDepth = getDepth(node.left)
    let rightDepth = getDepth(node.right)
    if (node.left === null && node.right !== null) {
      return 1 + rightDepth
    }
    if (node.left !== null && node.right === null) {
      return 1 + leftDepth
    }
    return 1 + Math.min(leftDepth, rightDepth)

  }
  return getDepth(root)

};

 222.完全二叉树的节点个数

参考资料（代码随想录）

题目

力扣题目链接

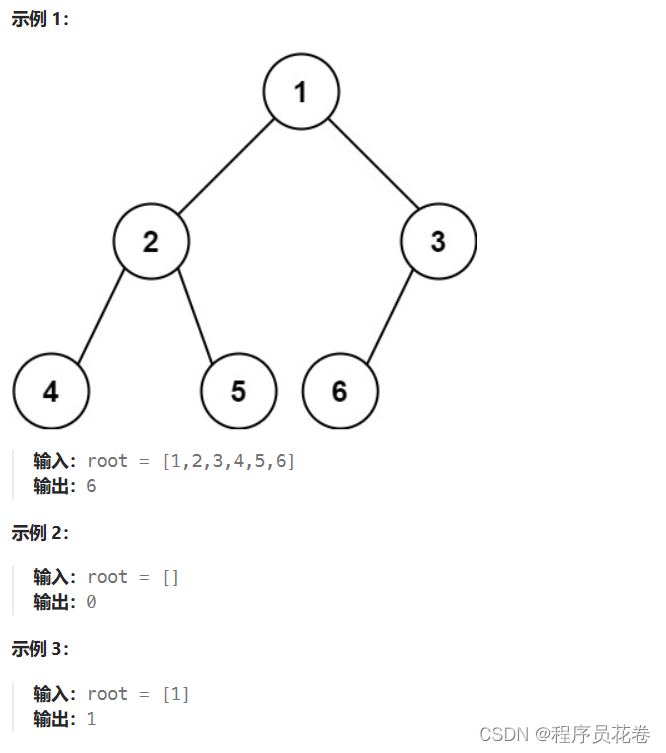
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

思路

本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。

普通二叉树

首先按照普通二叉树的逻辑来求，使用递归法来求，和求二叉树的深度写法类似。

递归遍历的顺序依然是后序（左右中）。

递归法

1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。
2. 确定终止条件：如果为空节点的话，就返回0，表示节点数为0。
3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

 代码如下（JavaScript）

var countNodes = function (root) {
  //递归法计算二叉树节点数
  //1.确定函数的参数 和 返回值
  const getNodeSum = function (node) {
    //2.确定终止条件
    if (node === null) return 0
    //3.确定单层逻辑
    let leftNum = getNodeSum(node.left)
    let rightNum = getNodeSum(node.right)
    return leftNum + rightNum + 1
  }
  return getNodeSum(root)
};

 完全二叉树

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

完全二叉树（一）如图：

完全二叉树（二）如图：

                                               

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

 代码如下（JavaScript）

var countNodes = function(root) {
    //利用完全二叉树的特点
    if(root === null) {
        return 0;
    }
    let left = root.left;
    let right = root.right;
    let leftDepth = 0, rightDepth = 0;
    while(left) {
        left = left.left;
        leftDepth++;
    }
    while(right) {
        right = right.right;
        rightDepth++;
    }
    if(leftDepth == rightDepth) {
        return Math.pow(2, leftDepth+1) - 1;
    }
    return countNodes(root.left) + countNodes(root.right) + 1;
};