Leetcode Day10 (恼人的子序列问题)

原创已于 2024-09-04 21:44:36 修改 · 368 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

于 2024-08-23 01:57:17 首次发布

leetcode 专栏收录该内容

24 篇文章

订阅专栏

647 回文子串的个数

class Solution:
    def countSubstrings(self, s: str) -> int:
        dp = [[False] * len(s) for _ in range(len(s))]
        result = 0
        for i in range(len(s)-1, -1, -1): #注意遍历顺序
            for j in range(i, len(s)):
                if s[i] == s[j]:
                    if j - i <= 1: #情况一 和 情况二
                        result += 1
                        dp[i][j] = True
                    elif dp[i+1][j-1]: #情况三
                        result += 1
                        dp[i][j] = True
        return result

5 最长回文也就迎刃而解了

class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp = [[False] * len(s) for _ in range(len(s))]
        maxlenth = 0
        left = 0
        right = 0
        for i in range(len(s) - 1, -1, -1):
            for j in range(i, len(s)):
                if s[j] == s[i]:
                    if j - i <= 1 or dp[i + 1][j - 1]:
                        dp[i][j] = True
                if dp[i][j] and j - i + 1 > maxlenth:
                    maxlenth = j - i + 1
                    left = i
                    right = j
        return s[left:right + 1]

300 最长上升子序列(不需连续)

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4

dp[i]指[0,i]中最长序列长度
状态转移方程: dp[i] = max(dp[j] + 1, dp[i])

674 最长连续递增子序列(需连续)

dp[i] = dp[i -1] + 1 if nums[i] > nums[i-1]

718 两个数组公共子序列的最大长度

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3, 2, 1]

我勒个丢, dp是真不好想, 但我用了一步转换之后, 思路豁然开朗
:我们把A竖着, 把B横着, 则可以创建

 B  3 2 1 4 7
A
1   0 0 1 0 0
2   0 1 0 0 0
3   1 0 0 0 0
2   0 1 0 0 0
1   0 0 1 0 0

我们只需要数沿着斜率为-1上最长的1的就可以了

class Solution:
    def findLength(self, nums1: List[int], nums2: List[int]) -> int:
        m, n = len(nums1), len(nums2)
        dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if nums1[i - 1] == nums2[j - 1]:
                    dp[i][j] = 1 + dp[i - 1][j - 1]
        return max(max(row) for row in dp)

注意拷贝的方法

115 不同的子序列

给你两个字符串 s 和 t ，统计并返回在 s 的子序列中 t 出现的个数，结果需要对 109 + 7 取模。
输入：s = “babgbag”, t = “bag”
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        n, m = len(s), len(t)
        
        # 如果 s 比 t 短，不可能包含 t
        if n < m:
            return 0
        
        # 初始化 dp 数组，增加一行一列用于处理空字符串的情况
        dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
        
        # 初始化第一列，空字符串 t 是任何字符串的子序列，次数为 1
        for i in range(n + 1):
            dp[i][0] = 1
        
        # 填充 dp 数组
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        
        # 返回右下角的值，即整个问题的解
        return dp[n][m]

132 相当于之前的所有结合起来

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是
回文串

返回符合要求的最少分割次数。

209 长度最小子数组s.t.之和大于target

class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        n = len(nums)
        l = 0
        sum = 0
        res = n + 1
        for i in range(n):
            num = nums[i]
            sum += num
            while (sum >= target):
                res = min(res, i - l + 1)
                sum -= nums[l]
                l += 1
        return res if res <= n else 0

713 同理

3 最长不含重复子串的长度

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        count = {}
        res = 0
        n = len(s)
        l = 0
        for r in range(n):
            c = s[r]
            count[c] = count.get(c, 0) + 1
            while count[c] > 1: # 注意这个地方是count[c]不是count[c[l]]
                count[s[l]] -= 1
                l += 1
            res = max(res, r - l + 1)
        return res

128 最长连续序列(1,2,3…)

class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        res = 1
        num_set = set(nums)
        for num in nums:
            if num - 1 in num_set:
                continue
            else:
                to_find = num + 1
                temp = 1
                while to_find in num_set:
                    to_find+=1
                    temp += 1
                res = max(res, temp)
        return res

好中好中好. 我们只考虑以num为开始的序列, 如果num-1在的话, 就直接跳过. 注意虽然有两个循环, 但是复杂度仍然是O(n)

560 和为k的连续子数组个数

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。

子数组是数组中元素的连续非空序列

不连续的话就变成背包问题了, 但这道题明显更复杂

第一反应:前缀+遍历 -> $O(n^2)$
第二反应: 前缀和+哈希set, 但怎么能使set呢, 前缀和可以出现重复的情况
第三正确反应: 用哈希表数count

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        res = 0
        prefix_sum = 0  
        
        # 这是为了处理从数组开始就满足条件的子数组
        dic = {0: 1}
        
        for i in range(n):
            prefix_sum += nums[i]
            
            # 检查是否存在一个之前的前缀和，使得当前前缀和减去它等于k
            target = prefix_sum - k
            res += dic.get(target, 0)
            
            # 更新当前前缀和的出现次数
            dic[prefix_sum] = dic.get(prefix_sum, 0) + 1
        
        return res

76 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

输入：s = “ADOBECODEBANC”, t = “ABC”
输出：“BANC”
解释：最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        def check(arr1, arr2):
            for i in range(len(arr1)):
                if arr1[i] - arr2[i] < 0:
                    return False
            return True

        n = len(s)
        m = len(t)
        t_count = [0] * 52
        s_count = [0] * 52
        for i in range(m):
            t_count[ord(t[i]) - ord('a')] += 1

        x, y = -1, -1
        ans = n + 1

        l = 0
        for r in range(n):
            c = s[r]
            s_count[ord(c) - ord('a')] += 1
            while (check(s_count, t_count)):
                if r - l + 1 < ans:
                    x, y = l, r
                    ans = r - l + 1
                s_count[ord(s[l]) - ord('a')] -= 1
                l += 1
        return s[x:y+1] if ans != n+ 1 else ""

主要思想是滑动窗口

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        ans_left, ans_right = -1, len(s)
        left = 0
        cnt_s = Counter()  # s 子串字母的出现次数
        cnt_t = Counter(t)  # t 中字母的出现次数
        for right, c in enumerate(s):  # 移动子串右端点
            cnt_s[c] += 1  # 右端点字母移入子串
            while cnt_s >= cnt_t:  # 涵盖
                if right - left < ans_right - ans_left:  # 找到更短的子串
                    ans_left, ans_right = left, right  # 记录此时的左右端点
                cnt_s[s[left]] -= 1  # 左端点字母移出子串
                left += 1  # 移动子串左端点
        return "" if ans_left < 0 else s[ans_left: ans_right + 1]

用Counter可以简化很多 , 这个>=操作太方便了lol

1143 最长公共子序列(可非连续)

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # dp[i][j] means i, j的公共序列长度
        n = len(text1)
        m = len(text2)
        dp = [[0] * (m + 1) for _ in range(n + 1)]
        
        # initialization
        # no need
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                if text1[i-1] == text2[j-1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j-1], dp[i-1][j], dp[i][j - 1])
        return dp[-1][-1]

一开始写的是 if text1[i] == text2[j], 超范围了, 改为[i-1] and [j-1], 因为我们定义不一样

32 最长合理括号(得连续)

class Solution:
    def longestValidParentheses(self, s: str) -> int:
        n = len(s)
        res = 0

        # ->
        l = r = 0
        for i in range(n):
            if s[i] == "(":
                l += 1
            else:
                r += 1
            if l == r:
                res = max(res, l + r)
            elif r > l:
                l = r = 0
            else:
                continue

        # <-
        l = r = 0
        for i in range(n-1, -1, -1):
            if s[i] == "(":
                l += 1
            else:
                r += 1
            if l == r:
                res = max(res, l + r)
            elif r < l:
                l = r = 0
            else:
                continue
        return res

比较巧妙, 左右各遍历一次就可以了

97 交错字符串

详情请看https://leetcode.cn/problems/interleaving-string/solutions/48146/dong-tai-gui-hua-zhu-xing-jie-shi-python3-by-zhu-3/?envType=study-plan-v2&envId=top-interview-150

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        len1=len(s1)
        len2=len(s2)
        len3=len(s3)
        if(len1+len2!=len3):
            return False
        dp=[[False]*(len2+1) for i in range(len1+1)]
        dp[0][0]=True
        for i in range(1,len1+1):
            dp[i][0]=(dp[i-1][0] and s1[i-1]==s3[i-1])
        for i in range(1,len2+1):
            dp[0][i]=(dp[0][i-1] and s2[i-1]==s3[i-1])
        for i in range(1,len1+1):
            for j in range(1,len2+1):
                dp[i][j]=(dp[i][j-1] and s2[j-1]==s3[i+j-1]) or (dp[i-1][j] and s1[i-1]==s3[i+j-1])
        return dp[-1][-1]

763 划分字母区间

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

输入：s = “ababcbacadefegdehijhklij”
输出：[9,7,8]
解释：
划分结果为 “ababcbaca”、“defegde”、“hijhklij” 。
每个字母最多出现在一个片段中。
像 “ababcbacadefegde”, “hijhklij” 这样的划分是错误的，因为划分的片段数较少。

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        start = {}
        end = {}        
        for i in range(len(s)):
            if s[i] not in start:
                start[s[i]] = i
            end[s[i]] = i
        intervals = []
        for c in s:
            intervals.append([start[c], end[c]])
        intervals.sort(key = lambda x:x[0])
        
        res = []
        for a, b in intervals:
            if not res:
                res.append([a, b])
                continue
            a1, b1 = res[-1]
            if a > b1:
                res.append([a, b])
                continue
            if b1 >= b:
                continue
            res[-1][1] = b

        return [interval[1] - interval[0] + 1 for interval in res]

一次写出来了, 先把它转换为区间问题, 就可以了

但是你看标答的解法, 太美丽了:

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        # 步骤1: 创建一个字典，记录每个字符最后出现的位置
        last = {c: i for i, c in enumerate(s)}
        
        # 初始化变量
        start = 0  # 当前分区的起始位置
        end = 0    # 当前分区的结束位置
        result = [] # 存储每个分区的长度
        
        # 步骤2: 遍历字符串，确定分区
        for i, c in enumerate(s):
            # 更新当前分区的结束位置
            # 取当前的end和字符c最后出现位置的较大值
            end = max(end, last[c])
            
            # 步骤3: 检查是否到达分区结束位置
            if i == end:
                # 如果当前索引等于end，说明找到了一个分区
                # 计算分区长度并添加到结果中
                result.append(end - start + 1)
                # 更新下一个分区的起始位置
                start = i + 1
        
        return result

918 环形数组的最大和

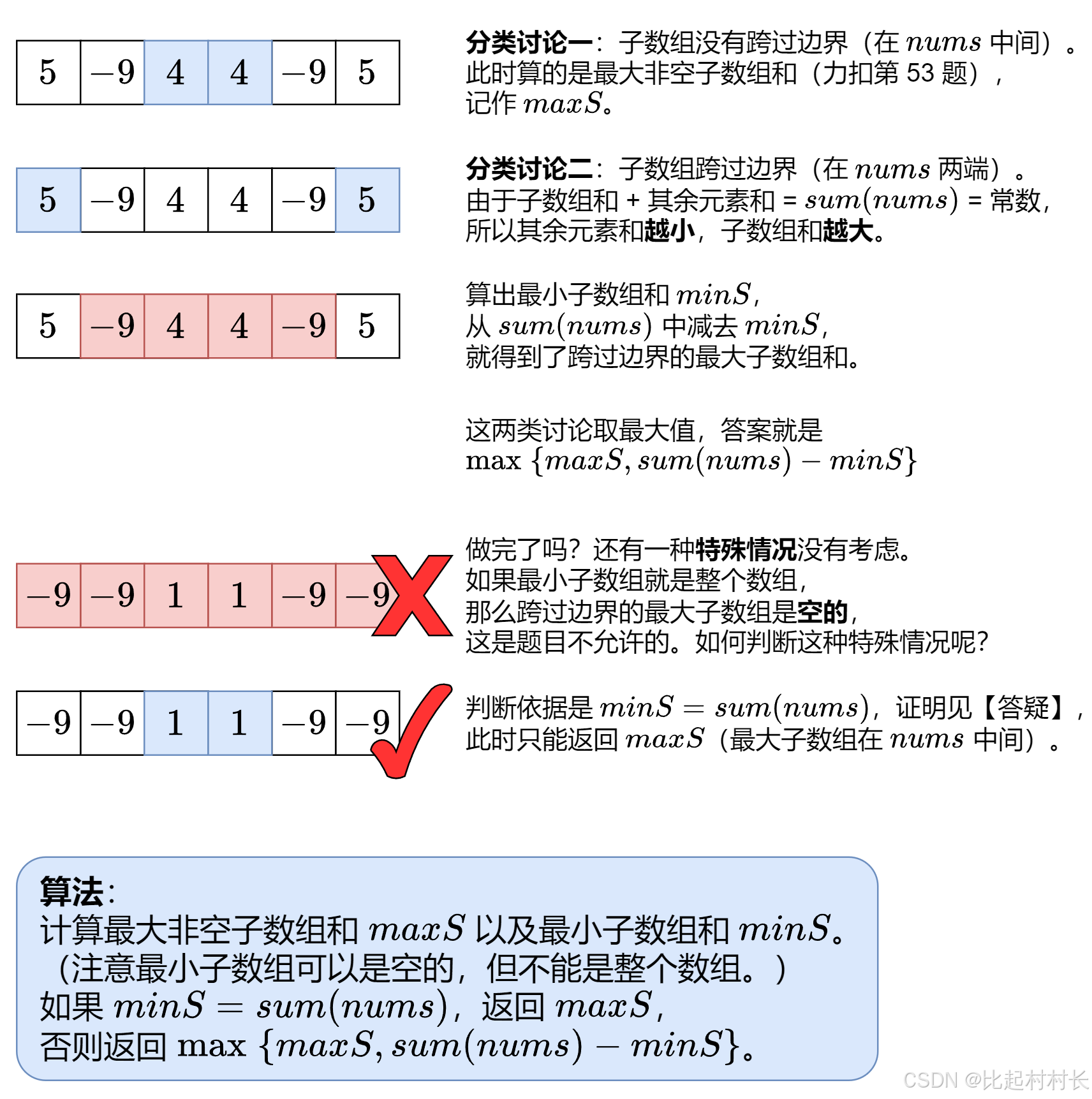
在这里插入图片描述

class Solution:
    def maxSubarraySumCircular(self, nums: List[int]) -> int:
        n = len(nums)
        
        # 初始化变量
        preMax, maxRes = nums[0], nums[0]  # preMax: 当前最大子数组和, maxRes: 全局最大子数组和
        preMin, minRes = nums[0], nums[0]  # preMin: 当前最小子数组和, minRes: 全局最小子数组和
        sum = nums[0]  # 整个数组的总和
        
        for i in range(1, n):
            # 更新最大子数组和
            preMax = max(preMax + nums[i], nums[i])
            maxRes = max(maxRes, preMax)
            
            # 更新最小子数组和
            preMin = min(preMin + nums[i], nums[i])
            minRes = min(minRes, preMin)
            
            # 计算整个数组的和
            sum += nums[i]
        
        # 如果最大子数组和为负数，说明所有数都是负数，直接返回最大子数组和
        if maxRes < 0:
            return maxRes
        else:
            # 否则，返回普通最大子数组和和环形最大子数组和中的较大值
            # 环形最大子数组和 = 总和 - 最小子数组和
            return max(maxRes, sum - minRes)