codeforce C. Ehab and Path-etic MEXs

题目大意：有一颗n个结点的树 ，现在让你分配每条边的权重，使得任意两个点之间的所有边的MEX值尽可能的小。

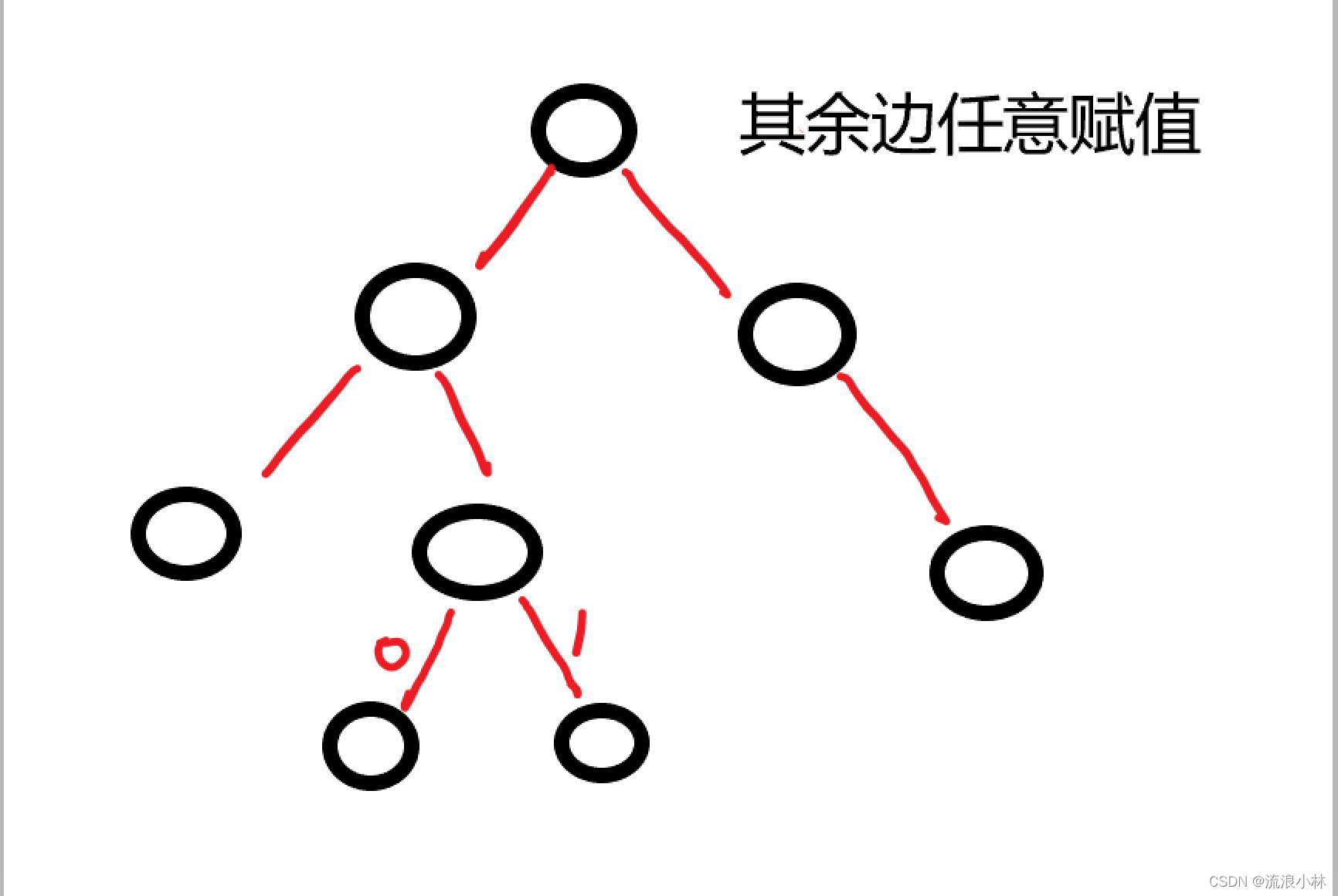
题解：寻找两个隶属于同一父亲的叶子节点，将两条边分别赋值为0和1，那么所有路径上的MEX值最大为1。显然由于0的存在，MEX不可能为0，所以1就是最小值。

 

#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
vector<int>g[maxn];
struct node {
	int u, v;
}e[maxn];
int main()
{
	int n, k;
	cin >> n;
	int x, y;
	for (int i = 1; i <= n - 1; i++)
	{
		cin >> x >> y;
		g[x].push_back(y);
		g[y].push_back(x);
		e[i].u = x;
		e[i].v = y;
	}
	int mx = n - 2, mi = 0;
	for (int i = 1; i < n; i++)
	{
		if (g[e[i].u].size() == 1 || g[e[i].v].size() == 1)
		{
			cout << mi++ << endl;
		}
		else cout << mx-- << endl;
	}

}