十、函数递归

什么是递归？

程序调用自身的编程技巧称为递归（ recursion）。

递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的 一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

递归策略：只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

递归的主要思考方式在于：把大事化小

递归的两个必要条件 ：

存在限制条件，当满足这个限制条件的时候，递归便不再继续。

每次递归调用之后越来越接近这个限制条件。

练习1：

接受一个整型值（无符号），按照顺序打印它的每一位。

例如： 输入：1234，输出 1 2 3 4

#include<stdio.h>
void print(unsigned int n)
{

	if (n>9)
	{
		print(n / 10);
	}
	printf("%d ", n % 10);
}
int main()
{
	unsigned int num = 0;
	scanf("%u", &num);
	print(num);

	return 0;
}

流程：

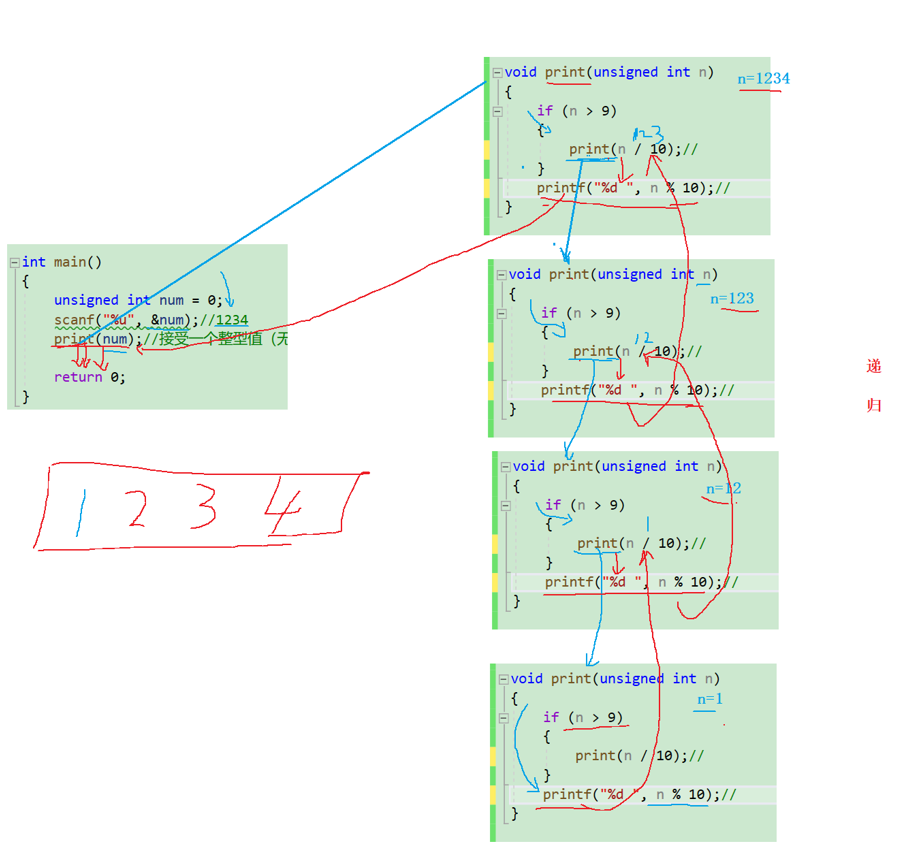
必须要有结束递归的条件，否则会死溢出。

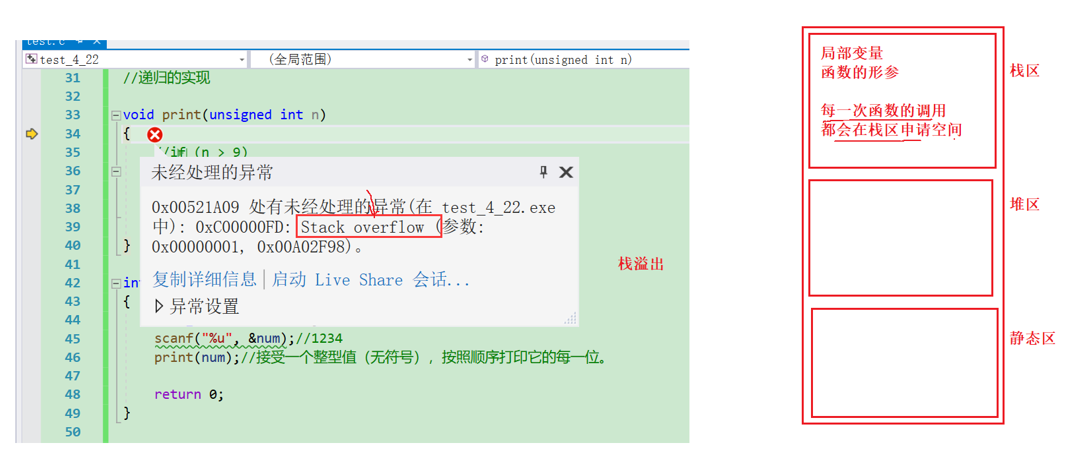
练习2 ：

编写函数不允许创建临时变量，求字符串的长度。

#include<string.h>
//int my_strlen(char  str[])//参数部分写成数组的形式
int my_strlen(char* str) //参数部分写成指针的形式
{
	int count = 0;//不允许创建临时变量
	while (*str != '\0')
	{
		count++;
		str++;//找下一个字符
	}
	return count;
}

int main()
{
	
	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d\n", len);
	return 0;

}

//递归求解
//my_strlen("abc");
//1+my_strlen("bc");
//1+1+my_strlen("c");
//1+1+1+my_strlen("");
//1+1+1+0
int my_strlen(char* str)
{
	if (*str !=  '\0')
		return 1 + my_strlen(str+1);//++str会改变值本身，而str+1只会改变函数识别到的地址
	else
		return 0;
}
int main()
{

	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d\n", len);
	return 0;

}

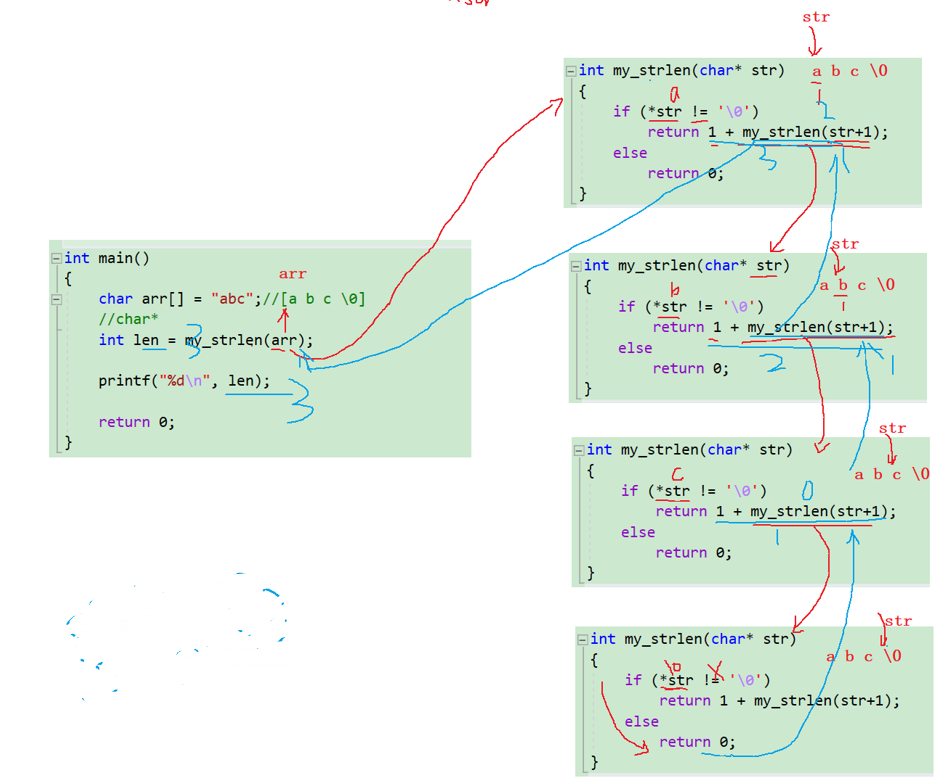
练习3：

求n的阶乘。（不考虑溢出）

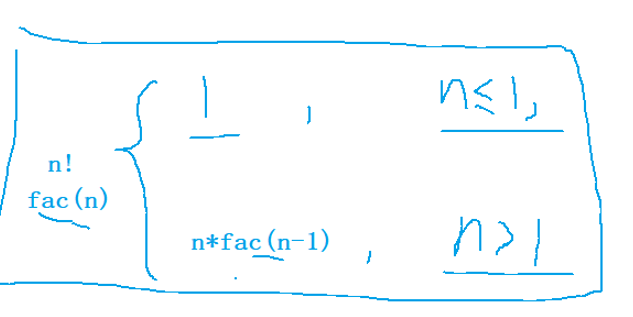
//递归实现
int fac(int n)
{
	if (n <= 1)
		return 1;
	else
		return n * fac(n - 1);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = fac(n);
	printf("ret = %d\n", ret);
	return 0;
}

//迭代的方式 - 非递归
int fac(int n)
{
	int i = 0;
	int ret = 1;
	for ( i = 1; i <=n; i++)
	{
		ret = ret * i;

	}
	return ret;
	
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = fac(n);
	printf("ret = %d\n", ret);
	return 0;
}

练习4：

求第n个斐波那契数。（不考虑溢出 ）

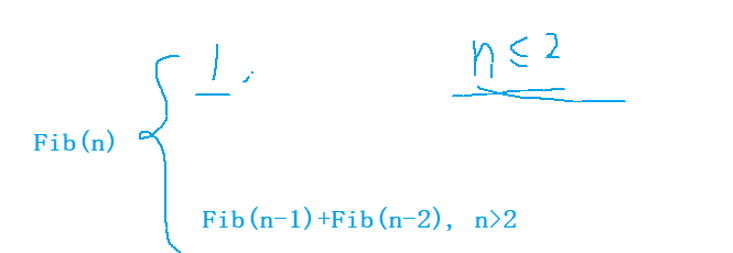
//求第n个斐波那契数。（不考虑溢出 ）
// 1 1 2 3 4 5 8 13 21 34 55...
//前两个数相加为第三个数
int Fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d\n", ret);

	return 0;
}

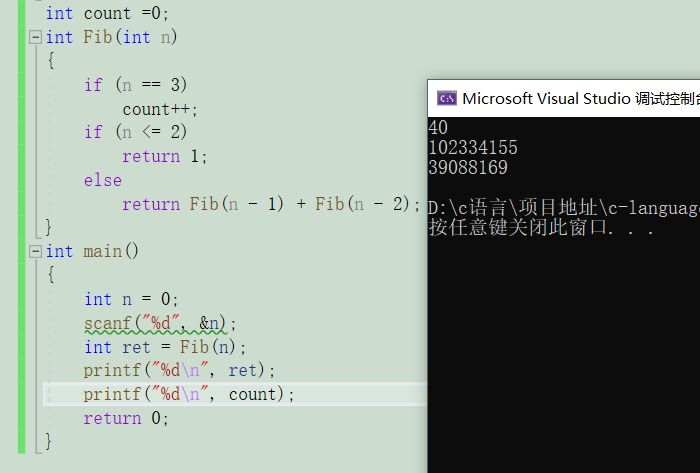
算了39088169次。

用迭代更块。

//迭代 - 非递归
int Fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;
	while (n>=3)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d\n", ret);

	return 0;
}

函数递归的几个经典题目（自主研究）：

1. 汉诺塔问题
2. 青蛙跳台阶问题