机械臂5次3次匀速插值轨迹规划

6自由度机械臂运动学分析与轨迹优化

1. 实验目的

1. 掌握 6自由度机械臂 的正向运动学和逆向运动学分析方法。

2. 实现 笛卡尔空间轨迹 的生成与优化，包括五项插值法、三次插值法和匀速优化方法。

3. 通过 MATLAB Robotics Toolbox 验证运动学分析的正确性，并对求解结果进行优化和验证。

2. 实验原理

2.1 正向运动学

正向运动学通过机械臂的 DH 参数 和 关节变量 计算末端执行器的位姿矩阵。

2.2 逆向运动学

逆向运动学通过末端执行器的 位姿矩阵 求解机械臂的 关节变量。使用数值解法（如 `ikunc` 函数）求解。

2.3 轨迹优化

1. 五项插值法：使用五次多项式插值生成平滑轨迹。

2. 三次插值法：使用三次多项式插值生成轨迹。

3. 匀速优化方法：使用匀速插值生成轨迹。

3. 实验步骤

1. 定义机械臂模型：

    使用改进的 DH 参数定义 6 自由度机械臂。

2. 生成笛卡尔空间轨迹：

    定义起始点和目标点，生成笛卡尔空间轨迹。

3. 轨迹优化：

    使用五项插值法、三次插值法和匀速优化方法优化轨迹。

4. 正向运动学验证：

    计算给定关节变量的末端执行器位姿矩阵。

5. 逆向运动学验证：

    从位姿矩阵求解关节变量，并重新计算位姿矩阵以验证解的准确性。

6. 轨迹分析与可视化：

    绘制轨迹曲线、速度曲线和加速度曲线，分析轨迹的平滑性和动态性能。

1. 实验结果

4.1 正向运动学验证

给定关节变量，计算末端执行器位姿矩阵：

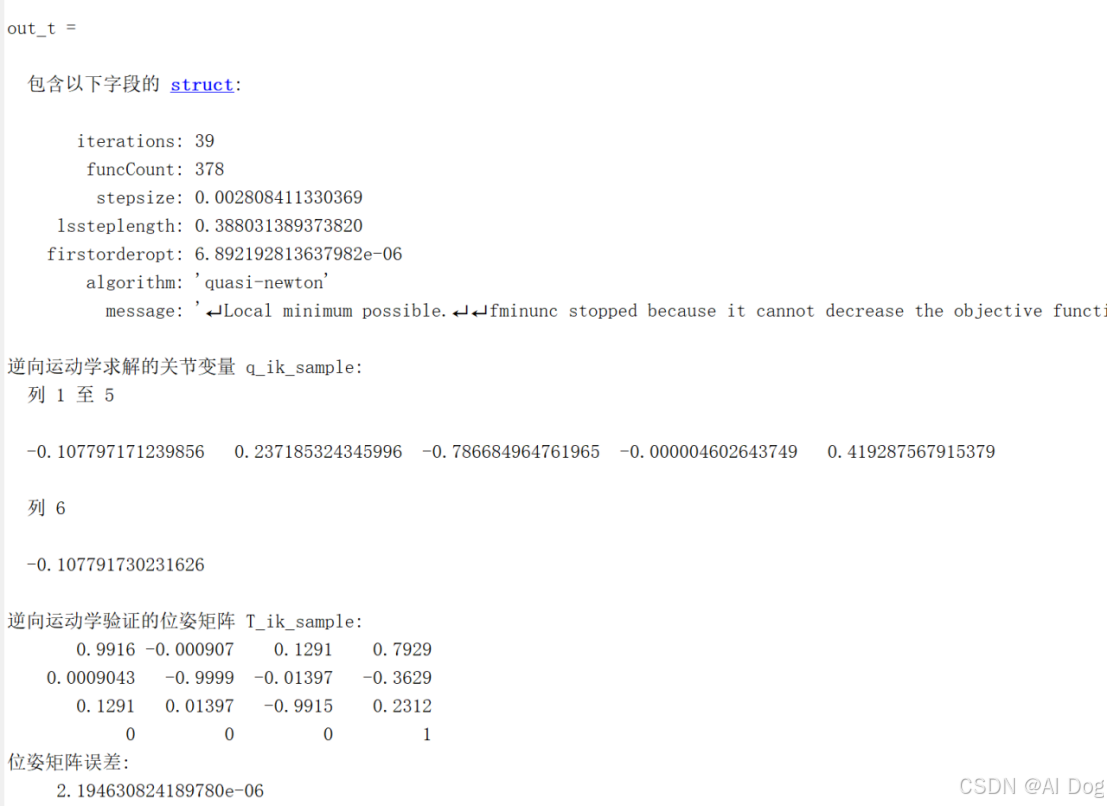
4.2 逆向运动学验证

从位姿矩阵求解关节变量：

4.3 轨迹优化结果

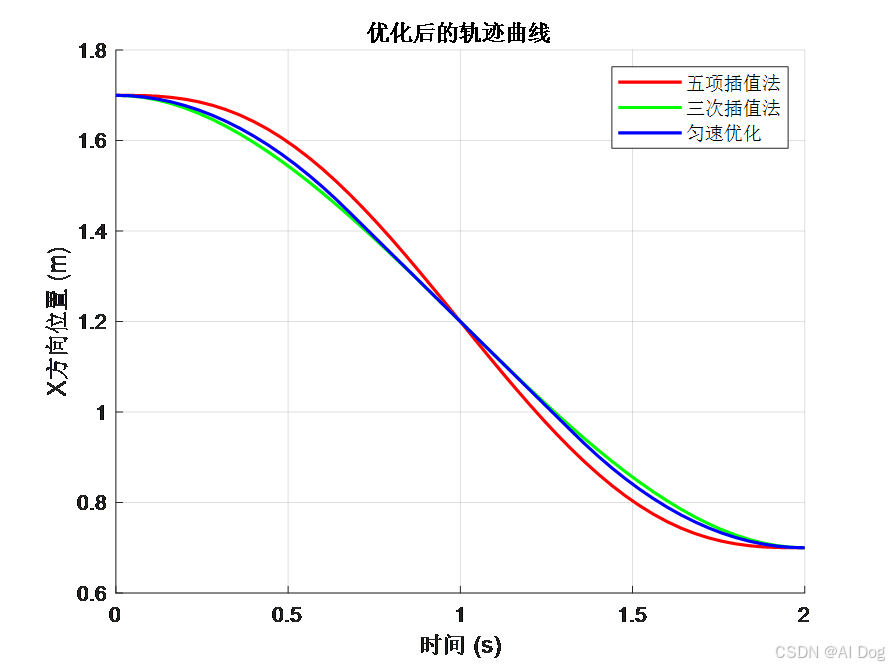
1. 轨迹曲线：

    五项插值法、三次插值法和匀速优化方法的轨迹曲线平滑。

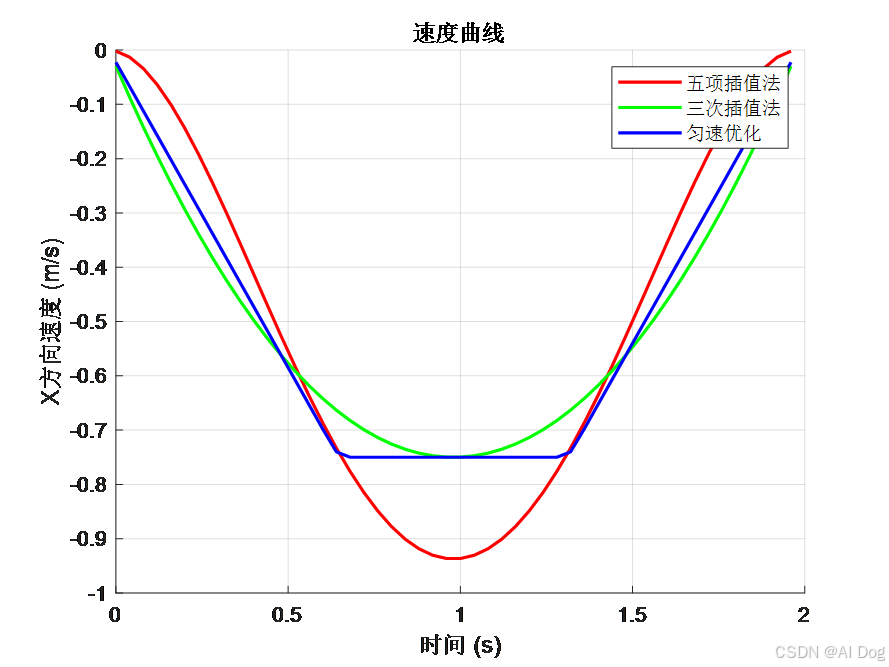
2. 速度曲线：

    五项插值法的速度曲线连续，三次插值法的速度曲线存在突变，匀速优化方法的速度恒定。

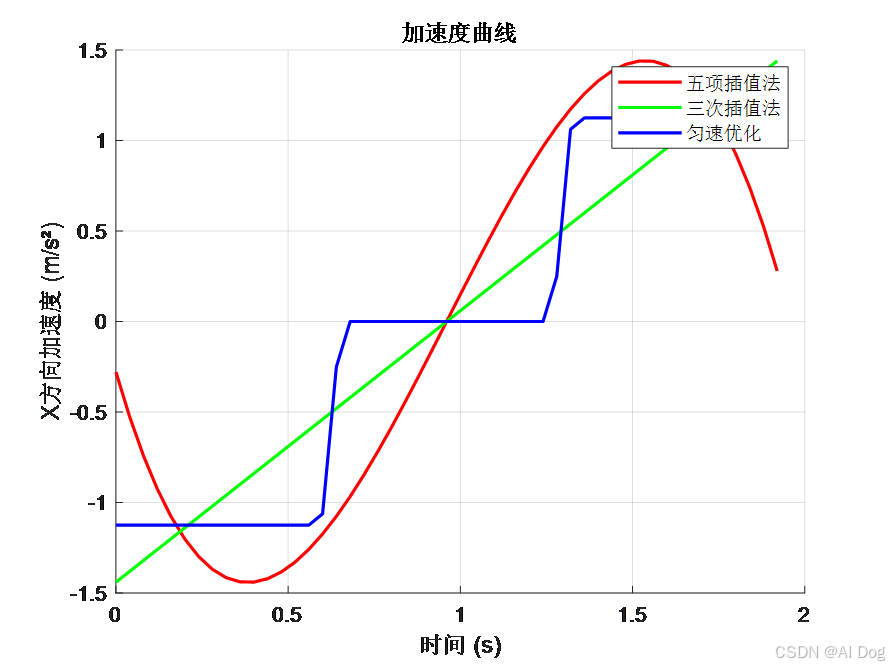
3. 加速度曲线：

五项插值法的加速度曲线连续，三次插值法的加速度曲线存在突变，匀速优化方法的加速度为零。

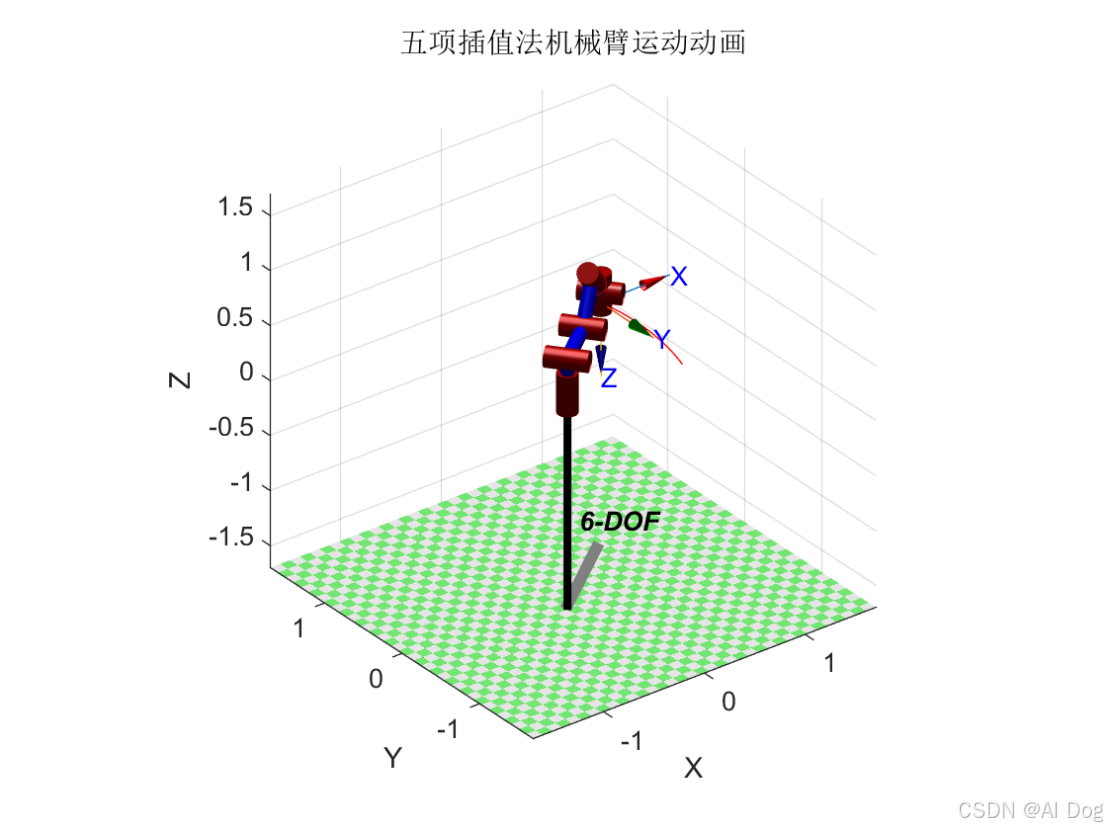
4.4 机械臂运动动画

1. 五项插值法：机械臂运动平滑，轨迹连续。

2. 三次插值法：机械臂运动存在轻微抖动。

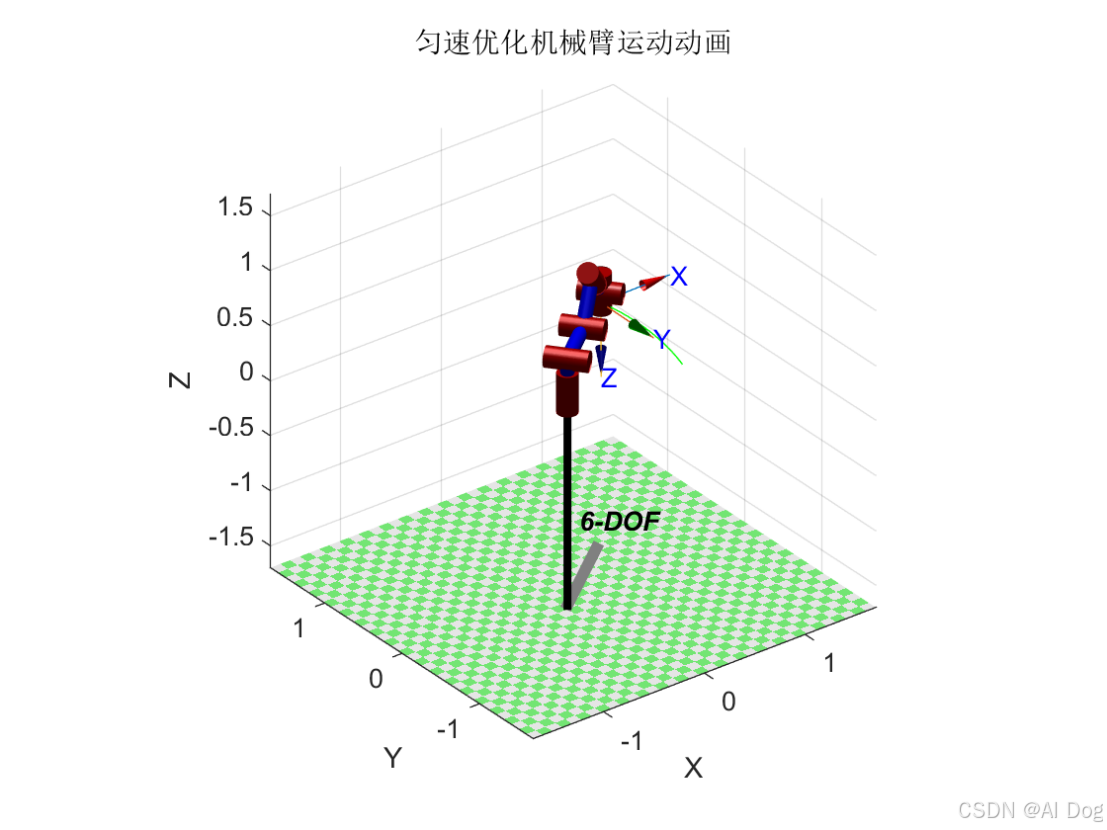
3. 匀速优化方法：机械臂运动匀速，轨迹平滑。

5. 实验总结

1. 正向运动学：

    通过 DH 参数和关节变量成功计算了末端执行器的位姿矩阵。

2. 逆向运动学：

    使用数值解法求解关节变量，验证了解的正确性。

3. 轨迹优化：

    五项插值法生成的轨迹平滑，适合高精度运动；三次插值法生成的轨迹存在突变，适合中等精度运动；匀速优化方法生成的轨迹匀速，适合匀速运动场景。

4. 误差分析：

    逆向运动学求解的误差接近于零，表明解的准确性。