‘ network communites’（网络社区）（一）（介绍和目标函数的建立）

引言：

在这个系列中，我们会大概介绍‘ network communites’里的所有内容，希望读者读完后对‘network communites’有基本的了解，需要了解全部的话，欢迎关注我的更新。

一：‘ network communites ’的引出：

首先，先给出一张这样的图：

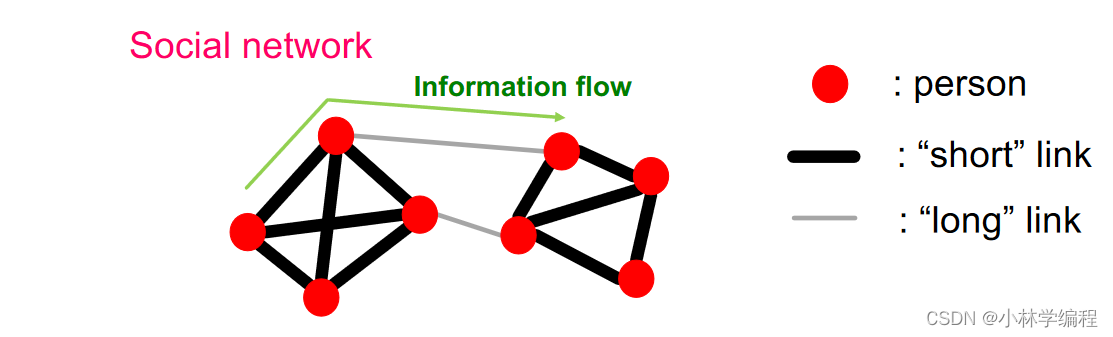
大家会发现在这张graph的结构中，出现了几个聚集的几个小区域，发现有的边是粗的，有些边是细的，那这些都代表什么含义呢？

我们可以先从社交网络的角度切入分析，红色的节点表示每一个不同的人，粗短的黑线可以用来表示我们很熟悉的人，长细的灰线可以用来表示交往联系较弱的人。

这里举一个例子，有一位斯坦福大学的教授曾经做过这么一个实验就是：一般人找到的工作基本上都是通过熟人介绍的，由此我们可以发现，周围的熟人对你有着重要的作用，回到这张graph中，我们也可以得到在粗黑线的连接（熟人）应该也会对，每一个人起到重要的作用。所以我们可以认为这些节点的嵌入是比较相似的。而灰细线的连接（一般熟的人）连接的是不同区域的人，可以认为节点的嵌入比较不相似。

pay attention：其中要注意一点强链接的边缘（黑粗线）的嵌入信息是比较冗余的（对于你选择的节点），而那些弱边缘（灰细线）的嵌入信息（对你选择的节点）是更加重要的，举个例子，因为强链接关系的都是熟人，圈子差不多，大家获得的信息比较一致，比较相似，所以新信息的获取就没这么多，而弱链接（一般朋友）你们处于的圈子不一样，相似度不高，所以你能获得到的新信息就更多。

当然，不只是社交网络，在不同网络的graph中也是会有类似社交网络这种graph的特点，举这些例子可以让我们更加直观的感受在网络中的集群的分布，和连接的作用。

现在，我们就能给出一个定义：如图，我们把这种相对集中的一个个‘小团体’称作‘network communites’（网络社区）。

二：‘network communites’目标函数：

   在神经网络模型的世界里，一般我们为了达到我们的模型能够使用，需要有一个目标函数，通过不断更新参数来使我们的模型能够使用，所以，在‘network communites’世界中，我们也需要有一个目标函数，是模型能够输出聚合效果。

   我们使用的目标函数称为Q（Modularity）（模块化）如下图所示：

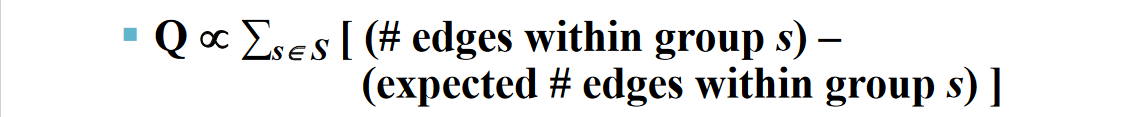
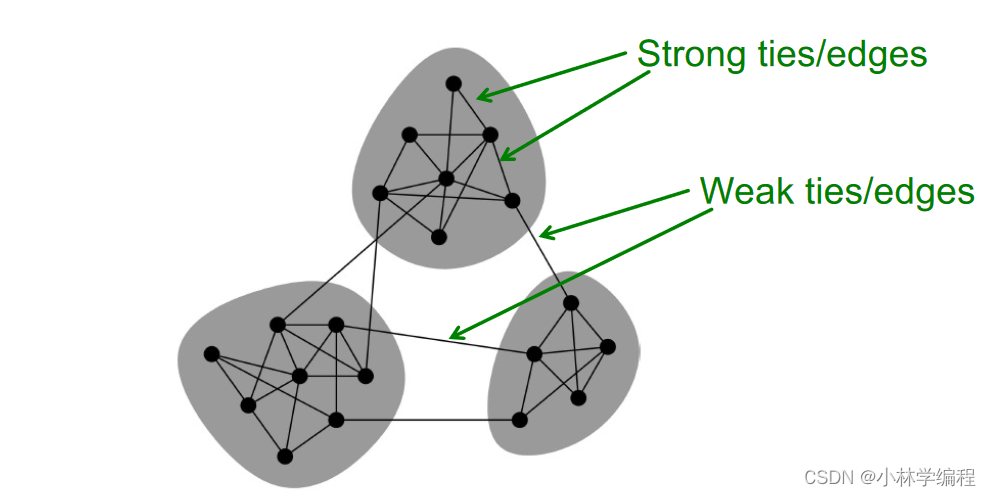
图中的S为图中中灰色部分的集合；s为一个灰色部分,后面是把每一个s中的（实际边-在s中期望的边）把每个集合得到的累加的结果。

如下图为具体使用的目标函数 Q：

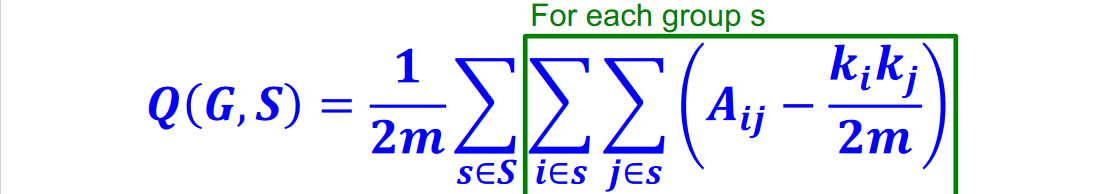
其中，（G，S）分表代表Graph，Graph中的集群集合（与上面的S定义相同）；

            m指实际上每一个s中的边（edge）总数，（1/2m）为归一化参数，使Q的函数值处于[-1,1]之间；

           i，j指的是两个s中的节点；

          表示为实际上i，j节点有无边连接，（有的话就是1，没有就是0）

          表示期望中的i，j节点有无连接（比如有0.65的概率有可能i，j节点有边）（其中表示i节点实际上的度即实际上的边数）

接下来我们的问题变成了，我们通过怎样的算法找到高Q分数的网络社区？（在接下来的系列（二）中）

五：系列传送门：

（二）：‘ network communites’（网络社区）（二）（louvain算法实现）_小林学编程的博客-优快云博客https://blog.youkuaiyun.com/weixin_57643648/article/details/123589236

（三）：

https://blog.youkuaiyun.com/weixin_57643648/article/details/123652501https://blog.youkuaiyun.com/weixin_57643648/article/details/123652501