图算法实战-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_57596714/article/details/122484022

图结构

第一题：无向图连通分量个数
第二题：有向图连通性判断
第三题：有向图最短边数 bfs
心得

第一题：无向图连通分量个数

[问题描述]
采用邻接表存储结构，编写一个求无向图的连通分量个数的算法。
[输入]
图的结点个数，图的边数，各边的起点以及终点
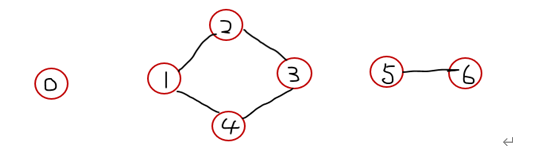
在这里插入图片描述
[输出]
图的连通分量
[存储结构]
邻接表
[算法的基本思想]
创建邻接表：按照邻接表的结构特点，将对应边及其对应点的关系进行确定。连通分量的计算：采用dfs遍历个点，得到连通子图的连通分量，在从中选取最大值，作为图的连通分量。

#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 10
#define NULL 0
typedef struct ArcNode{ //表结点
	int adjvex; //邻接点,数组下标 
	struct ArcNode *next; //下一个表结点 
}ArcNode, *anode;

typedef struct VNode{ //头节点 
	ArcNode *firstNode; //第一个邻接点 
}VNode;

typedef struct Graph{ //邻接表 
	VNode adjNode[MAXSIZE]; //头结点集
	int visit[MAXSIZE]; //初始值为0，被访问后变为1 
	int n; //顶点个数
	int e; //边数 
}Graph, *graph;

int num[MAXSIZE]; //记录不同结点的连通分量 

void creatGraph(graph &g){ //构造邻接表 
	g = (graph)malloc(sizeof(Graph));
	printf("请输入顶点个数和边数：");
	scanf("%d", &g->n); //记录结点数 
	scanf("%d", &g->e); //记录边数 
	int x, y, i;
	for(i = 0; i < MAXSIZE; i++){
		//初始化visit数组并且初始化第一个邻接点 
		g->visit[i] = 0;
		g->adjNode[i].firstNode = (anode)malloc(sizeof(ArcNode));
		g->adjNode[i].firstNode->next = NULL; //舍弃一个结点空间，作为头结点方便插入 
	}
	for(i = 0; i < g->e; i++){
		//遍历各边，创建对应的表结点 
		printf("请输入第%d条边的起点和终点：", i + 1);
		scanf("%d", &x); //记录起点 
		scanf("%d", &y); //记录终点 
		anode p = (anode)malloc(sizeof(ArcNode)); //因为是无向图 
		anode q = (anode)malloc(sizeof(ArcNode)); //所以同时有两个表结点生成
		p->adjvex = x;
		q->adjvex = y;
		p->next = g->adjNode[y].firstNode->next; //采用头插法 
		q->next = g->adjNode[x].firstNode->next;
		g->adjNode[y].firstNode->next = p;
		g->adjNode[x].firstNode->next = q;	
	}
}


int dfs(graph g, int x, int i){
	//采用dfs对一个指定结点开始进行遍历
	//i的作用保证num数组计数的稳定性，所以在整体的一次递归中i不变 
	g->visit[x] = 1; //标记为已访问 
	anode p = g->adjNode[x].firstNode->next;
	while(p != NULL){
		//对一个头结点后的表结点进行循环 
		if(g->visit[p->adjvex] == 0){
			//判断是否被访问(是否满足递归条件)
			num[i]++; //结点数的记录（连通分量的记录） 
			dfs(g, p->adjvex, i);
		}
		p = p->next;
	}
	return num[i];
}

int main(){
	graph g;
	creatGraph(g);
	int i, max = 0;
	for(i = 1; i < g->n; i++){
		//遍历每个结点，求出连通分量 
		num[i] = dfs(g, i, i);
		if(max < num[i]){
			//判断结点的最大连通分量，为图的连通分量 
			max = num[i];
		}
	}
	printf("连通分量为：%d", max + 1); //在求连通分量时，忽略了头结点，故加1 
}

结构演示：
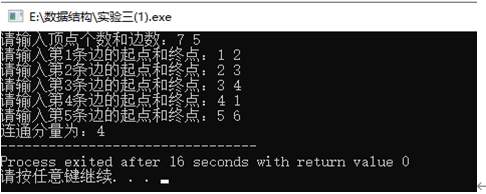
在这里插入图片描述
结果与分析：
优点：通过dfs完成了实验要求，对子图的连通分量均可进行计算，空间利用率较高。缺点：不易操作两点间的关系。时间复杂度：O(n*2e)，空间复杂度：O(n+2e)，n为图的结点个数，e为边数。

第二题：有向图连通性判断

[问题描述]
试基于图的深度优先搜索策略编写一程序，判别以邻接表方式存储的有向图中是否存在有顶点Vi到Vj顶点的路径(i≠j)。
[输入]
图的结点个数，图的弧数，各弧的起点以及终点，输入要判断的结点vi, vj。
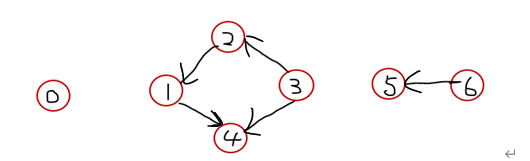
在这里插入图片描述
[输出]
若vi,vj之间存在路径为“vi, vj存在路径”
若vi,vj之间不存在路径为“vi, vj不存在路径”
[存储结构]
邻接表。
[算法的基本思想]
创建邻接表：按照邻接表的结构特点，将对应弧及其对应点的关系进行确定。是否存在路径的判断：采用dfs遍历vi点，若过程中有vj点存在则说明存在路径，若过程中没有vj则说明不存在路径。

#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 10
#define NULL 0
typedef struct ArcNode{ //表结点
	int adjvex; //邻接点,数组下标 
	struct ArcNode *next; //下一个表结点 
}ArcNode, *anode;

typedef struct VNode{ //头节点 
	ArcNode *firstNode; //第一个邻接点 
}VNode;

typedef struct Graph{ //邻接表 
	VNode adjNode[MAXSIZE]; //头结点集
	int visit[MAXSIZE]; //初始值为0，被访问后变为1 
	int n; //顶点个数
	int e; //边数 
}Graph, *graph;


void creatGraph(graph &g){ //构造邻接表 
	g = (graph)malloc(sizeof(Graph));
	printf("请输入顶点个数和边数：");
	scanf("%d", &g->n); //记录结点数 
	scanf("%d", &g->e); //记录边数 
	int x, y, i;
	for(i = 0; i < MAXSIZE; i++){
		//初始化visit数组并且初始化第一个邻接点 
		g->visit[i] = 0;
		g->adjNode[i].firstNode = (anode)malloc(sizeof(ArcNode));
		g->adjNode[i].firstNode->next = NULL; //舍弃一个结点空间，作为头结点方便插入 
	}
	for(i = 0; i < g->e; i++){
		//遍历各边，创建对应的表结点 
		printf("请输入第%d条边的起点和终点：", i + 1);
		scanf("%d", &x); //记录起点 
		scanf("%d", &y); //记录终点 
		anode p = (anode)malloc(sizeof(ArcNode)); //因为有向图，所以只需一个表结点 
		p->adjvex = y;
		p->next = g->adjNode[x].firstNode->next;//采用头插法 
		g->adjNode[x].firstNode->next = p;	
	}
}

int flag = 0; //利用flag记录是否访问到过y 
void dfs(graph g, int x, int y){
	//采用dfs对一个指定结点开始进行遍历
	g->visit[x] = 1; //标记为已访问 
	anode p = g->adjNode[x].firstNode->next;
		while(p != NULL){
			//对一个头结点后的表结点进行循环 
			if(g->visit[p->adjvex] == 0){
				//判断是否被访问(是否满足递归条件)
				if(p->adjvex == y){
					//判断是否可以经过y 
					flag = 1;
				}
				dfs(g, p->adjvex, y);
			}
			p = p->next;
		}
}

int main(){
	graph g;
	creatGraph(g);
	printf("请输入要判断的俩个结点，不能为同一结点：");
	int x, y;
	scanf("%d", &x);
	scanf("%d", &y);
	if(x != y){
		dfs(g, x, y);
		if(flag == 1){
			printf("V%d，V%d存在路径", x, y); 
		}
		else{
			printf("V%d，V%d不存在路径", x, y); 
		}
	}
	else{ 
		printf("输入不合法");
	}
}

结过演示：
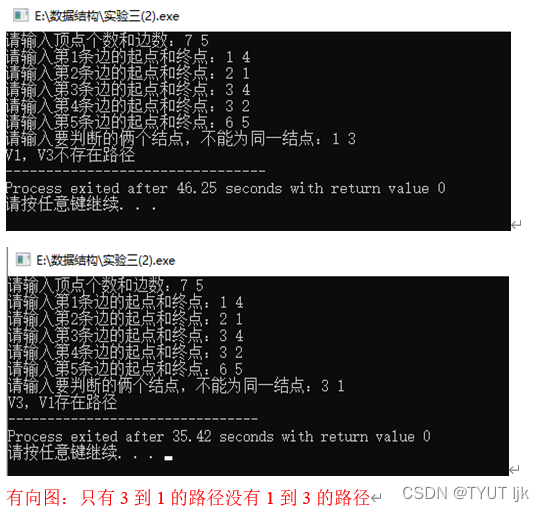
在这里插入图片描述
结果与分析：
优点：在第一题的基础上进行改造，将无向图的结构改为有向图，通过dfs判断是否经过点确定两点间有无路径。缺点：对于特殊情况的处理措施较少。时间复杂度：O(n*e)，空间复杂度：O(n+e)，n为图的结点个数，e为弧数。

第三题：有向图最短边数 bfs

[问题描述]
给定一个图，设计一个程序，找出一条从某一顶点A到另一顶点B边数最少的一条路径。要求使用邻接表方式实现。
[输入]
图的结点个数，图的弧数，各弧的起点以及终点，输入要判断的结点vi, vj。
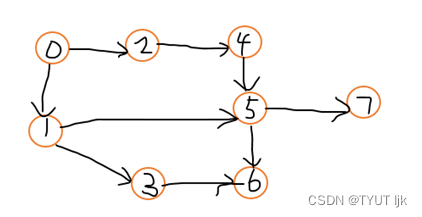
在这里插入图片描述
[输出]
若A到B无路径，则输出“A，B间不存在路径”，否则输出A到B路径上各顶点。
[存储结构]
邻接表。
[算法的基本思想]
创建邻接表：按照邻接表的结构特点，将对应弧及其对应点的关系进行确定。是否存在路径的判断：创建队列结构采用bfs遍历A点，若过程中有B点存在则说明存在路径且为最短路径，若过程中没有vj则说明不存在路径。使用num数组

#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 10
#define NULL 0
typedef struct ArcNode{ //表结点
	int adjvex; //邻接点,数组下标 
	struct ArcNode *next; //下一个表结点 
}ArcNode, *anode;

typedef struct VNode{ //头节点 
	ArcNode *firstNode; //第一个邻接点 
}VNode;

typedef struct Graph{ //邻接表 
	VNode adjNode[MAXSIZE]; //头结点集
	int visit[MAXSIZE]; //初始值为0，被访问后变为1 
	int n; //顶点个数
	int e; //边数 
}Graph, *graph;

int num[MAXSIZE]; 
//通过num数组进行bfs遍历时，该结点对应的连接点的记录，方便回溯 
void creatGraph(graph &g){ //构造邻接表 
	g = (graph)malloc(sizeof(Graph));
	printf("请输入顶点个数和边数：");
	scanf("%d", &g->n); //记录结点数 
	scanf("%d", &g->e); //记录边数 
	int x, y, i;
	for(i = 0; i < MAXSIZE; i++){
		//初始化visit数组并且初始化第一个邻接点 
		g->visit[i] = 0;
		g->adjNode[i].firstNode = (anode)malloc(sizeof(ArcNode));
		g->adjNode[i].firstNode->next = NULL; //舍弃一个结点空间，作为头结点方便插入 
	}
	for(i = 0; i < g->e; i++){
		//遍历各边，创建对应的表结点 
		printf("请输入第%d条边的起点和终点：", i + 1);
		scanf("%d", &x); //记录起点 
		scanf("%d", &y); //记录终点 
		anode p = (anode)malloc(sizeof(ArcNode)); //因为有向图，所以只需一个表结点 
		p->adjvex = y;
		p->next = g->adjNode[x].firstNode->next;//采用头插法 
		g->adjNode[x].firstNode->next = p;	
	}
}

void bfs(graph g, int A){ //采用广度优先进行遍历 
	ArcNode *p;
	int queue[MAXSIZE]; //创建队列记录结点 
	int front = 0; //队列初始化 
	int rear = 0;
	g->visit[A] = 1; //结点被访问 
	queue[rear++] = A; //结点入队 
	while(front != rear){
		//判断队列是否为空 
		p = g->adjNode[queue[front]].firstNode->next;
		while(p != NULL){ 
			//遍历一个头结点的表结点 
			if(g->visit[p->adjvex] == 0){
				//是否满足入队条件 
				g->visit[p->adjvex] = 1;
				num[p->adjvex] = queue[front]; //使用num记录其bfs遍历时的相连结点 
				queue[rear++] = p->adjvex;
			}
			p = p->next;
		}
		front++;
	}
}


int main(){
	graph g;
	creatGraph(g);
	printf("请输入要判断最短路径的俩结点：");
	int A, B;
	scanf("%d", &A);
	scanf("%d", &B);
	bfs(g, A);
	int i;
	i = num[B]; //查看使用bfs遍历时，B的直接关联结点 
	printf("%d", B);
	while(true){
		//通过对num数组的遍历可以确定A到B的完整路径 
		if(i == A){
			//若找到A,路径完成，退出 
			break;
		}
		else
		printf("<-%d", i);
		i = num[i];
	}
	printf("<-%d", A);
}

结果演示：
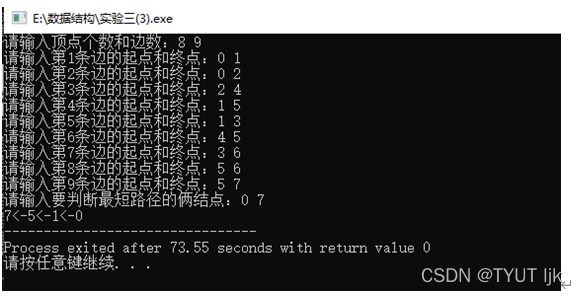
在这里插入图片描述
结果与分析：
优点：使用num数组记录bfs遍历时的直接相连结点，解决了输出路径的问题。缺点：若存在同样短的路时，只能判断随机一条，对特殊没有路径的情况没有判断。时间复杂度：O(n*e)，空间复杂度：O(n+e)，n为图的结点个数，e为弧数。

心得

学会了使用邻接表的存储方式对图进行存取。
邻接表的理解：邻接表由头结点集，以及表结点组成，则头结点集可通过头节点数据类型的数组实现，而表结点可通过单个申请空间获得。无向图一个边，对应两个表结点，通过头结点与表结点之间建立类似链表的关系，便可实现边的表示。
头结点中的firstNode指针可以看作类似于链表中的头结点，为了方便插入表结点时使用头插法，故舍弃一个结点空间，方便操作。
dfs遍历图的理解：图的深度优先遍历与树的先序遍历类似，在树中，可以通过左右子树实现递归规模的控制，而在图中有多个分支，就需要while(p != NULL)与p = p->next来进行图的递归规模的控制，在树的非递归中我使用过flag来记录左右子树是否被访问过，那么在图中同样也需要visit数组判断结点是否被访问过。把图dfs中经过的边保留，其余边删去，就可得到图的生成树。
判断两点间是否存在路径，只需对起点经行dfs遍历，通过遍历过程中有无经过终点，便可判断有无路径存在。
bfs遍历图的理解：bfs类似于树的层次遍历，需要队列的数据结构进行辅助实现（队列可以是int型，而非结点的数据类型，因为数组下标可以代表图中结点）。在图为非加权图时，bfs的遍历顺序其实就是两点最短路径的结点次序。
最短路径：在bfs在每次遍历时：一次出队列的结点与因为其出队列而入队列的结点的是相连接，要解决的问题就是记录对应结点是因为那个结点而入队的，在此题中使用了一个全局变量num进行记录，在根据对num的访问使用终点，逆推到起点便可得到最短路径。