JavaSE -- 方法（下）--浅谈递归

前言

上次在C语言阶段，笔者（笔者菜鸟起飞）就一直想写一篇关于递归的文章，来初步总结一下自己的思路，但是后面由于各种各样的事情耽搁后来想法就搁浅了，这次到JAVA可算给我逮着机会了！！！！

PS：可能知识比较浅，但是会尽力写好！！

一丶浅谈递归概念

首先，何为递归？

定义：一个方法在执行过程中调用自身, 就称为 “递归”

初步理解的话，可以用民间流传的口头文学的这样一个小故事来理解：

从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事，讲的什么呢？ 讲的是：从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事…

这里的话，就可以理解为一种不太健全的递归，因为他在讲故事的过程中不断地重复自身这一点和递归很像，但是为什么说他不健全？因为他没有结束条件！

在日常中，递归的思想也广为应用，比如数学解题方法上的“数学归纳法”，比如算法里面的"二分法查找"…

最后用一句大白话来总结递归：

大事化小，小事化了！

二丶递归的三要素

<1>明确目的 / 明确功能

故事总要有个开头，就比如《青玉案·元夕》，你不蓦然回首，你咋会知道她就在灯火阑珊处呢？所以我们在一开始就要有目的，如下题：

递归求 N 的阶乘！

我们的目的是求阶乘，所以：

//这里是求阶乘的！！！
public static int factor(int n) {

}

是的，先定义一个漂亮的方法名，然后开始我们的征程！

<2>明确终止条件

递归方法不能停不下来（停不下来这不没了！），所以我们要明确它的终止条件。也就是说，我们要能知道当参数为何值时，递归结束，并且我们能直接知道这个参数的返回值。例：

// 算 n 的阶乘(假设n不为0)
int factor(int 1){
        return 1;
}

对吧，我们可以很清楚地知道，当n = 1的时候，n的阶乘就等于1，那是不是就只能取值 n = 1呢？当然不是。

如果你知道任意参数的返回结果，你就可以把它设置为结束条件！

例如：

// 算 n 的阶乘(假设n不为0)
int factor(int 3){
        return 6;

3的阶乘就是6嘛~，理想情况下当然可以把n = 3作为结束条件（此时 n > 3）,当然我这里的取值都是理想状态，在代码中还是要严谨一些的。

<3>等价关系式

这一步就是重点啦，什么叫做大事化小，小事化了，说的就是这个！一步步深入，不断缩小参数范围，直到遇到终止条件！
比如我们上面的这个题，我们想要求 n! ，那么 n! = n * (n - 1)! , (n - 1)! = (n - 1)*(n - 2)!..以此类推
换到上面的题目中，就是：

return n *factor(n-1);

那么，完整的方法如下：

public static int factor(int n) {
 if (n == 1) {
	 return 1;
 }
 	 return n * factor(n - 1); //此时调用函数自身
}

我这里设置了参数为 1 作为终止条件，当然其他参数也可以，根据n的取值来确定。

三丶递归案例分析

感觉自己感刚刚学会开小三轮，就要被逼上路了，而且这个小破路还是山路，笔者的未来的计划就是成为造轮子的大佬，然后开着飞机飞，这多有B格！！芜湖起飞~

案例一： 按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4)

其实如果说是只能用循环来正序打印，笔者自己尝试过，真挺麻烦！！但是用递归，就方便很多。
三板斧走起：

第一步：明确函数自身目的—打印数字每一位

public static void print(int num) {
}

第二步： 明确终止条件—最后一位数字打印完成就结束

这里的话，笔者想提一下笔者做题时候总结出来的小经验：

如果一个整形数字想要去掉最后一位：就 /10 ，如果整数数字想得到最后一位：就 %10
所以结束条件就是 num / 10 == 0的时候，就剩最后一位啦，这一位打印结束。就不能再继续打印了

public static void print(int num) {
 if(a < 9) {
           System.out.print(a % 10 + " ");
       }
}

第三步：等价关系式
这一步的话，明确过程到底干了什么，就像这一题中，一边输出最后一位数，一边给自身赋值除去最后一位数字的其余数：

 if(a < 9) {
           System.out.print(a % 10 + " ");
       }else {
           print(a / 10);
           System.out.print(a % 10 + " ");

案例二：递归求 1 + 2 + 3 + … + 10

很简单，三板斧！！！！

第一步：明确函数自身目的—求和

  //求和
  public static int sum(int a){
     
    }

第二步： 明确终止条件—n = 1的时候，就没数字可以加了

  //求和
  public static int sum(int a){
        if(a == 1){
            return 1; 
        }
    }

第三步：等价关系式
这里的话说起来有点绕，就是 10 + 9+…+1 = 10 + （9 + … + 1）= 10 + 9 + （8 + … + 1）…

如下：

 public static int sum(int a){
        if(a == 1){
            return 1;
        }
        return a + sum(a - 1);
    }

笔者认为递归其实最难得点就在第三步和其中的细节把控，多少次因为一个变量设置不到位就被一直卡到死。

案例三：求斐波那契数列的第 N 项

什么叫做斐波那契数列，就是一个数列从第三项开始，任意一项等于前两项之和：1 ，1， 2 ，3 ，5 ，8…

第一步：明确函数自身目的—求n项数字

//这里是求斐波那契数列第n项
public static int fib(int n) {

}

第二步： 明确终止条件—n = 1或者 n = 2的时候，就停止计算了

//这里是求斐波那契数列第n项
public static int fib(int n) {
	if(a == 1 || a == 2){
            return 1;
        }
}

第三步：等价关系式

任意一项都等于前两项之和，也就是 fib(n) = fib (n - 1) + fib (n -2)，而 fib(n-1) = fib( n - 2) + fib( n - 3),fib(n - 2) = fib( n - 3) + fib ( n - 4)…

//这里是求斐波那契数列第n项
public static int fib(int n) {
	if(a == 1 || a == 2){
            return 1;
        }
        return fib(a - 2) + fib(a - 1);
}

PS：关于斐波那契数列的进阶—迭代

在上面的案例三种，我们可以发现，如果说当n取值过大的之后，需要等很长很长一段时间后答案才会出来，甚至可以说出不来，这是为什么呢？

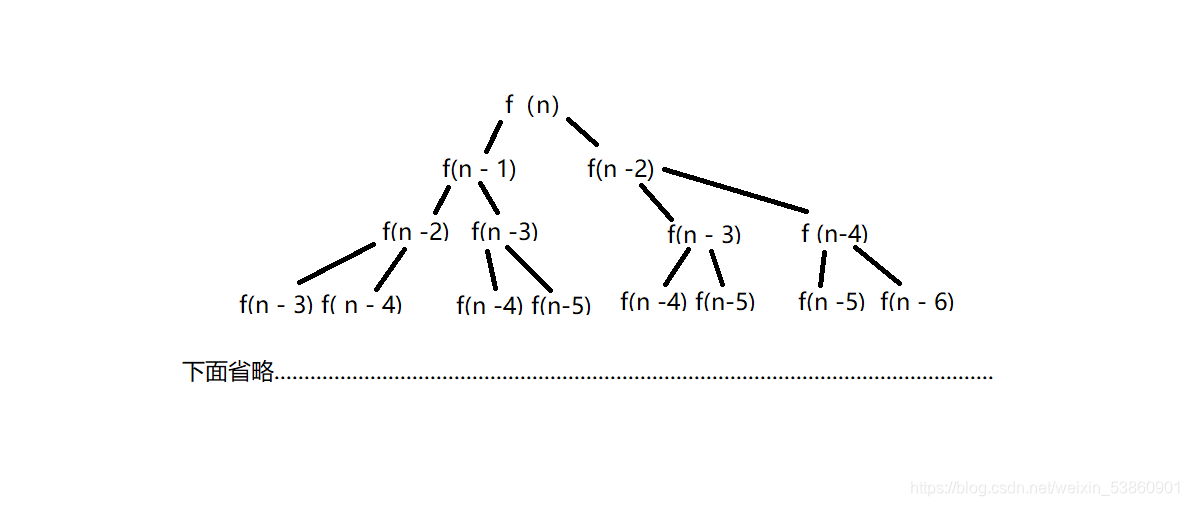
由图可以看出，每进行一层，运算的量都是呈2的指数倍上升，这是一个很可怕的事情，当n数字小的时候，还能用递归，数字大了呢？？所以就不行了。
那么我们怎么办呢？

递归是从上到下，我们可以从下到上呀！，然后每个位数就执行一次，这种从下到上的思想叫做迭代，也可以叫做递推。

那么具体该怎样实现呢？很简单，因为每一项的前两项之和等于其本身，所以，三板斧走起：

第一步—明确自身目的—求第n项和

public static int fib(int n) {
	
}

第二步—明确终止条件—当求到第n项时停止计算停止计算

       for (int i = 1; i <= n; i++) {
                
            }
        }
        return res;

第三步—等价关系式—每一项等于前两项相加

这一步较为特殊，因为第一项和第二项前面没有两项，所以真正应该从第三项算起，前两项的话要拉出来特别声明

 public static int fab(int n){
        int res = 0;
        int key1 = 1;
        int key2 = 1;
        if(n == 1 || n == 2){
          return 1;
        }else{
            for (int i = 3; i <= n; i++) {
                res = key1 + key2;
                key1 = key2;
                key2 = res;
            }
        }
        return res;
    }

综上，就是关于在这一章节递归的应用，希望大家可以指正。