基础算法(acw)_acw算法-优快云博客

该笔记为学习记录笔记(学习自acw网站y总)，基础算法部分包括（每天都要好好学习认真做笔记啊啊啊）

排序
二分
高精度
前缀和与差分
双指针算法
位运算
离散化
区间合并

争取在2022.4.25之前将这部分学完，在此立下flag -- 4.15留

排序

快速排序

主要思想--分治

步骤：

确定分界点：q[l]，q[(l+r)/2]，q[r]随机
调整范围：左边<=x，右边>=x
递归处理左右两边

暴力替代：开辟两个数组，小于等于x的放在a[]，大于x的放在b[]。

代码模板：

#include<iostream>

using namespace std;

 const int N=1e6+10;
 
 int n;
 int q[N];
 
 void quick_sort(int q[],int l,int r)
 {
 	//判断边界 当l==r时递归结束 
 	if(l>=r) return;
 	
 	int x=q[l],i=l-1,j=r+1;
 	
 	// 将>=q[l]的都放在右边，把 <q[l]的都放在右边 
 	while(i<j)
 	{
 		do{i++;}while(q[i]<x);
 		do{j--;}while(q[j]>x);
 		if(i<j) swap(q[i],q[j]);
	}
	
	quick_sort(q,l,j);
	quick_sort(q,j+1,r);
 	
 }
 
 int main()
 {
 	scanf("%d",&n);
 	for(int i=0;i<n;i++)
 	{
 		scanf("%d",&q[i]);
	}
	
	quick_sort(q,0,n-1);
	
	for(int i=0;i<n;i++) printf("%d ",q[i]);
 	
 	return 0;
 }

归并排序

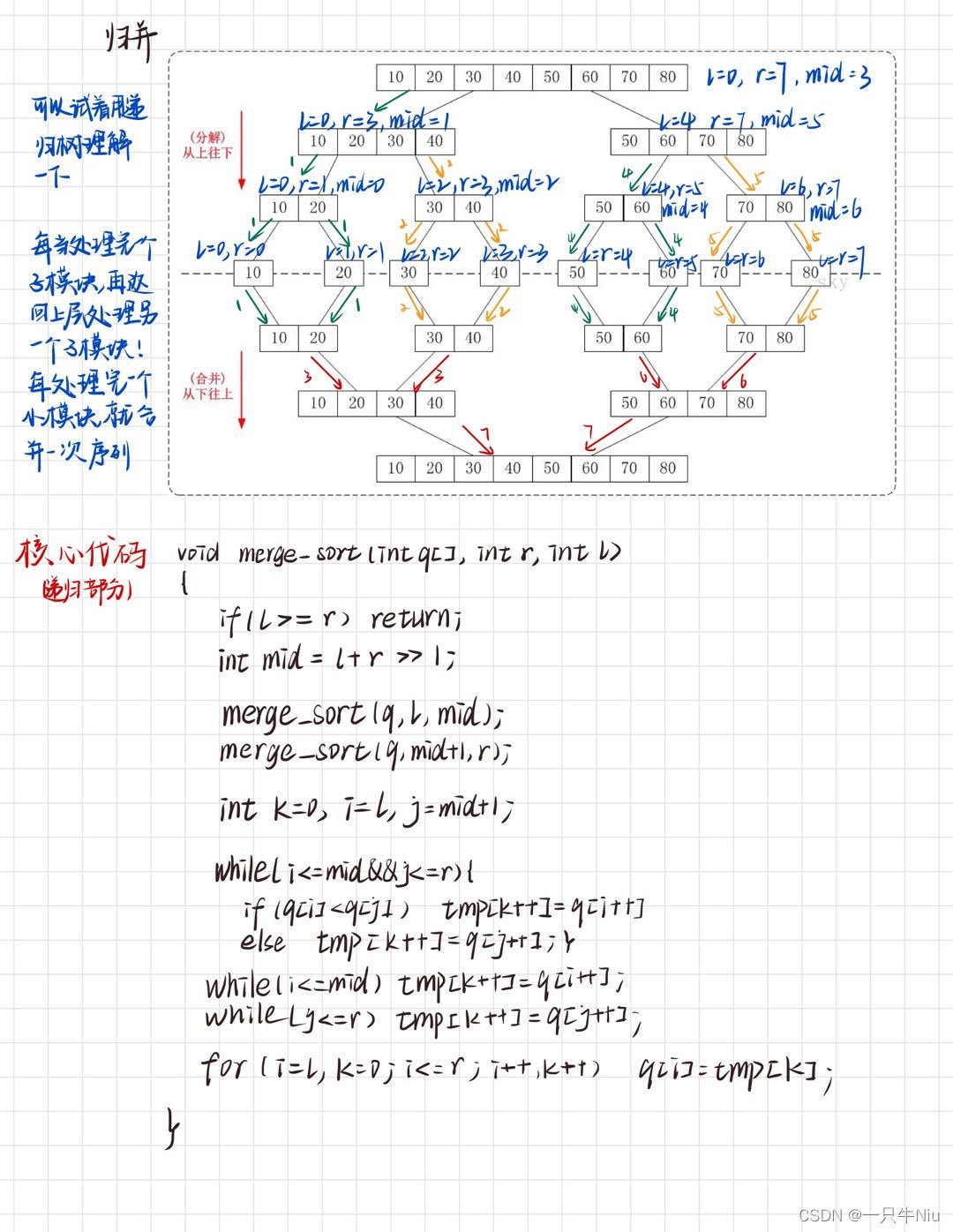
主要思想--分治

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

步骤：

确定分界点：mid=(l+r)/2

递归排序左边和右边

左边和右边会变成两个有序的序列，那咱们就把两边归并——合二为一！

运用了双指针算法，最后相当于合并两个有序数组。

思路分析：

int i=l,j=mid+1,k=0;

其中：i为左边序列第一个数，j为右边序列第一个数，k为临时数组的下标

这个大佬总结的真的很好！！

归并排序 - 如果天空不死 - 博客园概要本章介绍排序算法中的归并排序。内容包括：1.归并排序介绍2.归并排序图文说明3.归并排序的时间复杂度和稳定性4.归并排序实现4.1 归并排序C实现4.2 归并排序C++实现4.3 归并排序Javahttps://www.cnblogs.com/skywang12345/p/3602369.html#a42代码模板：

#include<iostream> 
using namespace std;

const int N=1000010;

int n;
int q[N];
int tmp[N];

void merge_sort(int q[],int l,int r)
{
	if(l>=r) return ;
	
	int mid=l+r>>1;
	
	//递归排序左右两边！ 
	//先排左边，再排右边，最后一层将两个段间有序的子序列依次排序
	//实在理解不了，可以画一个递归树 
	merge_sort(q,l,mid);
	merge_sort(q,mid+1,r);
	
	//i指向左边序列的起点，mid为左边序列的终点，j指向右边序列的起点，r为右边序列的终点 
	//k为临时区域的索引 
	int k=0,i=l,j=mid+1;
	while(i<=mid&&j<=r)
	{
		if(q[i]<=q[j]) 
			tmp[k++]=q[i++];
		else 
			tmp[k++]=q[j++];
	}
	//当两个数组任意一个还没比较完
	while(i<=mid) 
		tmp[k++]=q[i++];
	while(j<=r) 
		tmp[k++]=q[j++];
	
	//将排序好的元素，全部整合到数组q中 
	for(i=l,j=0;i<=r;i++,j++) 
		q[i]=tmp[j]; 
}


int main()
{
	cin>>n;    //n个数进行排序
	for(int i=0;i<n;i++) scanf("%d",&q[i]);
	
	merge_sort(q,0,n-1);
	
	for(int i=0;i<n;i++) printf("%d ",q[i]);
	
	return 0;
	
}

二分

整数二分

题目详情：

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

分析：

整数二分包含两个模板：一个找左端点，一个找右端点

左端点模板：

int mid=l+r>>1;

while(l<r){

if(check(mid)) r=mid;

else l=mid+1;

}

右端点模板：

int mid=l+r+1>>1;

while(l<r){

if(check(mid)) l=mid;

else r=mid-1;

}

代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N=10010; 
int n;	//n个数 
int k;	//k个询问 
int q[N];

int main()
{
	cin>>n;	
	cin>>k;
	for(int i=0;i<n;i++) cin>>q[i];
	

	while(k--)
	{
		int x;
		cin>>x;
		
		int l=0,r=n-1;
		//先找左端点 
		while(l<r)
		{
			int mid=l+r>>1;
			if(q[mid]>=x) r=mid;
			else l=mid+1;
		} 
		//当左端点存在时，继续找右端点，否则输出"-1 -1" 
		if(q[r]==x)
		{
			cout<<r<<" ";
			l=r,r=n-1;	//此时左边边界为刚刚找到的左端点，右边边界为数组的最后一个数 
			while(l<r)
			{
				int mid=l+r+1>>1;
				if(q[mid]<=x) l=mid;
				else r=mid-1;
			}
			cout<<l<<endl;
		}
		else cout<<"-1 -1";
		
	}
	
	return 0;
}

实数二分

题目详情：

给定一个浮点数 n，求它的三次方根。

输入格式

共一行，包含一个浮点数 n。

输出格式：

共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围

−10000≤n≤10000

输入样例：

1000.00
输出样例：

10.000000

代码：

#include<iostream>
using namespace std;

double n;

int main()
{
	cin>>n;
	double l=-10000,r=10000;
	
	//另一种写法，不管精度，直接给它循环100次
	//for(int i=0;i<100;i++) 
	while(r-l>1e-8)
	{
		double mid=(l+r)/2;
		if(mid*mid*mid>=n) r=mid;
		else l=mid;
	}
	
	printf("%.6lf",r);
	
	return 0;
}

高精度

★高精度运算★_一只牛Niu的博客-优快云博客目录高精度加法A+B高精度乘法A*B高精度加法A+B题目详情：输入两个整数，求这两个整数的和是多少。输入格式输入两个整数A,B，用空格隔开输出格式输出一个整数，表示这两个数的和数据范围0≤A,B≤10^8样例输入：3 4样例输出：7分析：1、大数加法，要注意越界问题，所以我们要用数组存储数A、B2、如何用数组存储A、B呢？首先，我们把A、B设置为字符串变量读入，再将A、B从低位到高位，依次存入数组，即低位先.https://blog.youkuaiyun.com/weixin_53461714/article/details/124015741?spm=1001.2014.3001.5501

前缀和

★二分与前缀和★_一只牛Niu的博客-优快云博客目录①二分数的范围数的三次方根机器人跳跃问题四平方和①二分一般如果题目的答案在一个有序区间，且具有两段性，即在它前面的数据满足一个性质，而在它后面的性质也满足一个性质，即可用二分法数的范围题目详情：给定一个按照升序排列的长度为n的整数数组，以及q个查询。对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。如果数组中不存在该元素，则返回-1 -1。输入格式第一行包含整数n和q，表示数组长度和询...https://blog.youkuaiyun.com/weixin_53461714/article/details/123976767?spm=1001.2014.3001.5501

差分

假设a1，a2，a3，... ，an为前缀和数组

构造b1，b2，b3，...，bn差分数组

使得b[i]=a[i]-a[i-1]

即an=b1+b2+b3+ ··· bn

相当于求前缀和的逆过程

作用：用O(1)的时间给原数组的某一段区间里的每个数都加上一个常数

如让一个数组的区间[l,r]所有的数都加上常数c，则只需要让 b[l]=b[l]+c,b[r+1]=b[r+1]-c，那么它的前缀和数组a[l]~a[r]每个数都会加上c，而a[r+1]及之后的数并不会发生改变。那么我们要的答案便是通过差分数组b求出的前缀和！

那么如何构造这个差分数组呢？其实不需要特意构造，逐步插入就好了！即对[i,i](i=1,2,...,n)区间都进行b[i]=b[i]+c,b[i+1]=b[i+1]-c操作：
void insert(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}

for(int i=1;i<=n;i++) insert(i,i,a[i]);
小tips：两个数组并没有实时联动起来，对某一个数组进行操作后需要手动操作同步

题目详情：

输入样例：

6 3

1 2 2 1 2 1

1 3 1

3 5 1

1 6 1

输出样例：

3 4 5 3 4 2

一些解释：

b[N]：是a[N]的差分数组，后面的b[i]+=b[i-1]相当于在求b的前缀和，即更新后的a[N]

a[N]：是b数组的前缀和，也是本题输入的原数组

其实在本题中，完全没有必要开a数组，只是为了更加方便理解

比较难理解的地方：对b数组的操作！！在求前缀和时我们新开一个数组a来记录我们输入的数组的前缀和，使得a[n]=b[1]+b[2]+···+b[n]，而在求差分时，我们新开一个数组b使得b[i]=a[i]-a[i-1]。

代码：

#include <iostream>
using namespace std;

const int N = 100010;
int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);

    while (m -- )
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }

    for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];

    for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);

    return 0;
}