最小生成树概念及其典型应用

首先，概念回顾：

生成树：包含所有顶点，但只包含部分边，因为要求树中不存在回路。

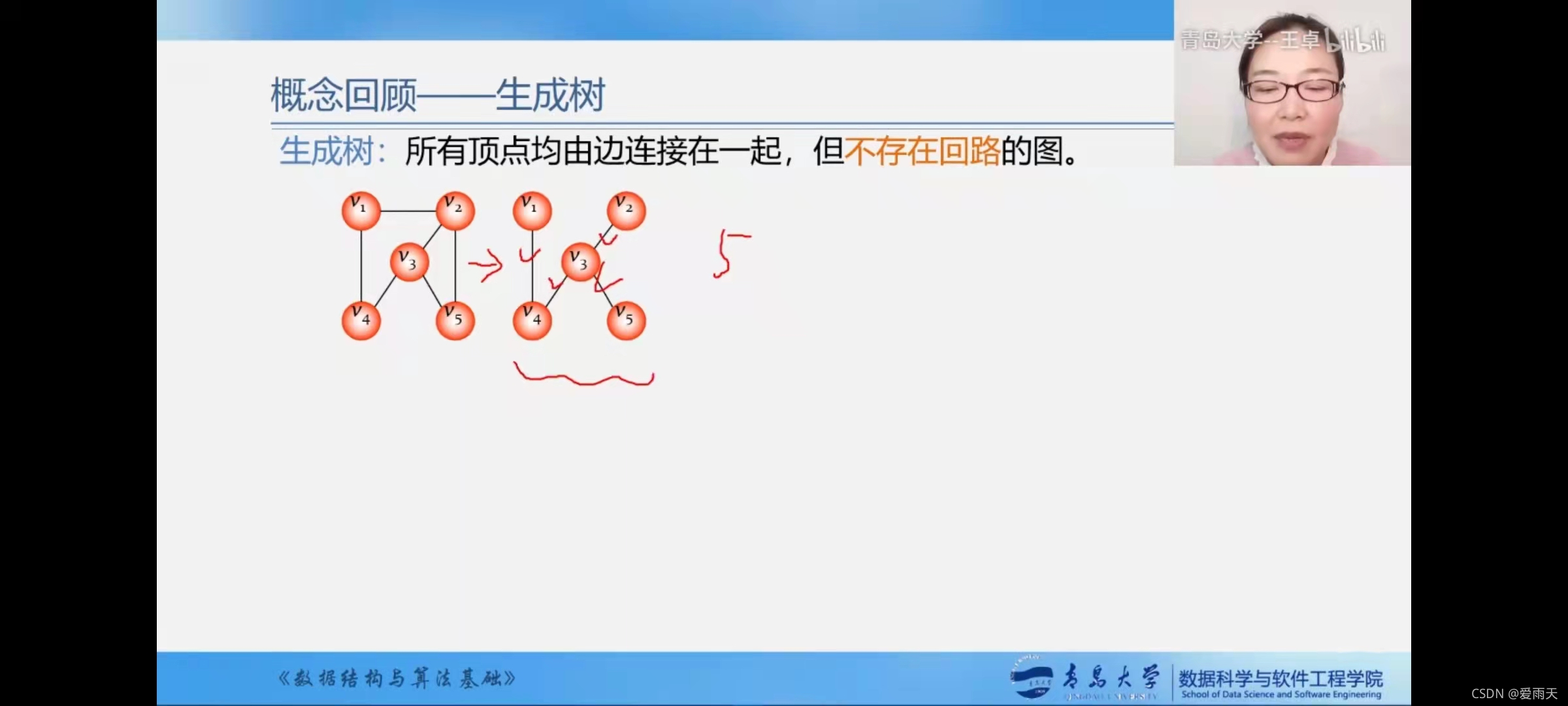
部分边不能多，也不能少，他少了，顶点就不能连接在一起了，它必须是连通的；它不能多，它随便找一条边就出现回路。

生成树共同特点：

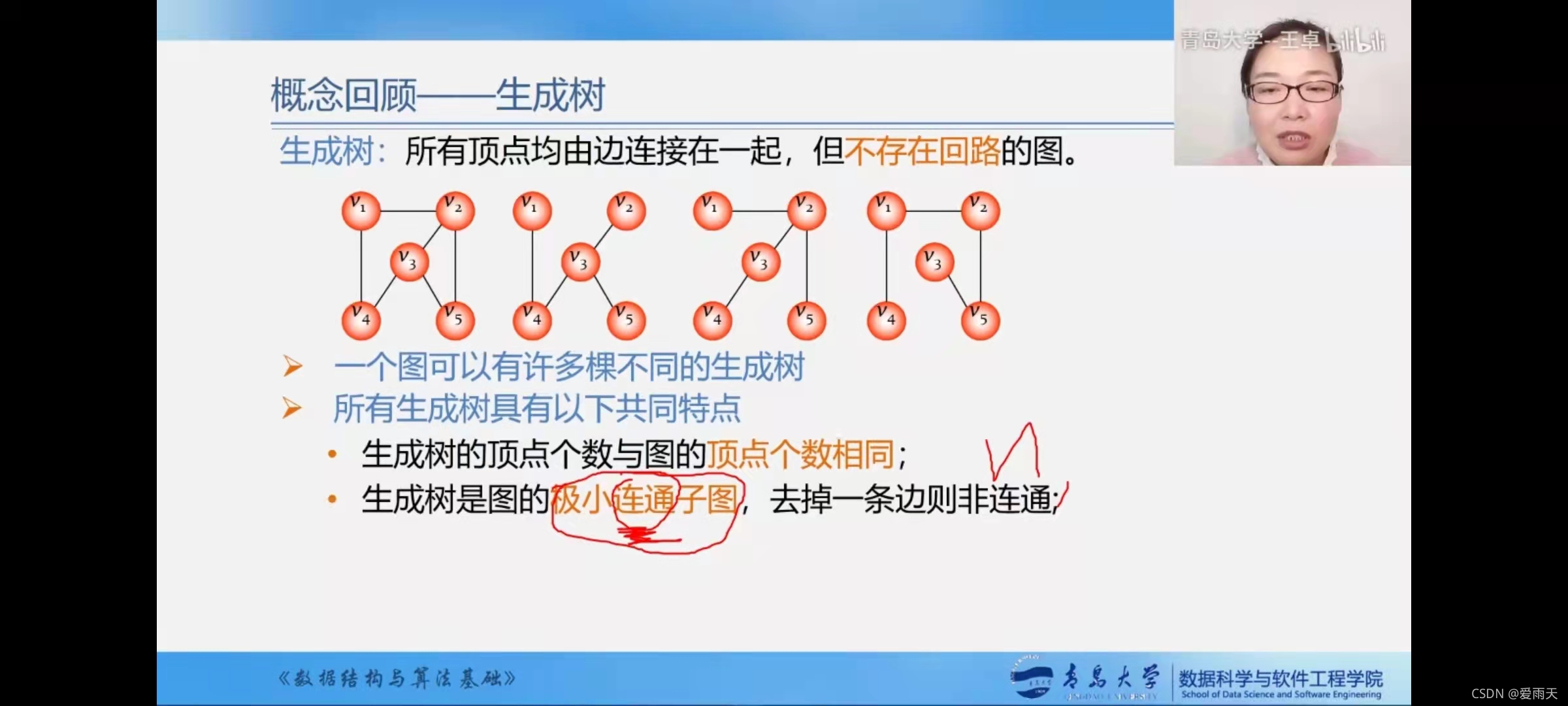
顶点数相同；

极小：边的数目少得不能再少了，再少一条边，就不连通了，就不是连通的子图了

连通且没有回路，就必然n个顶点的生成树，一定有n-1条边。

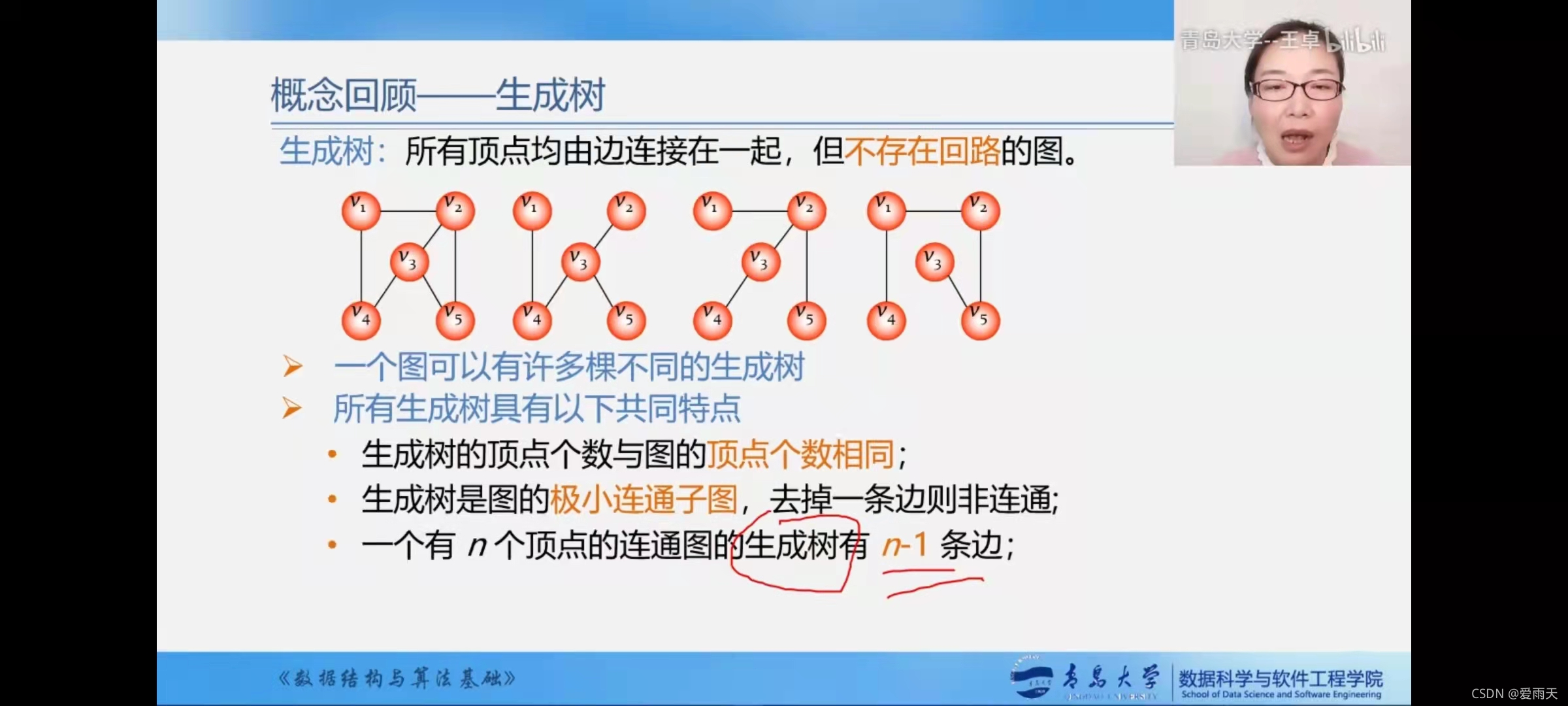
既要连通，又要没有回路

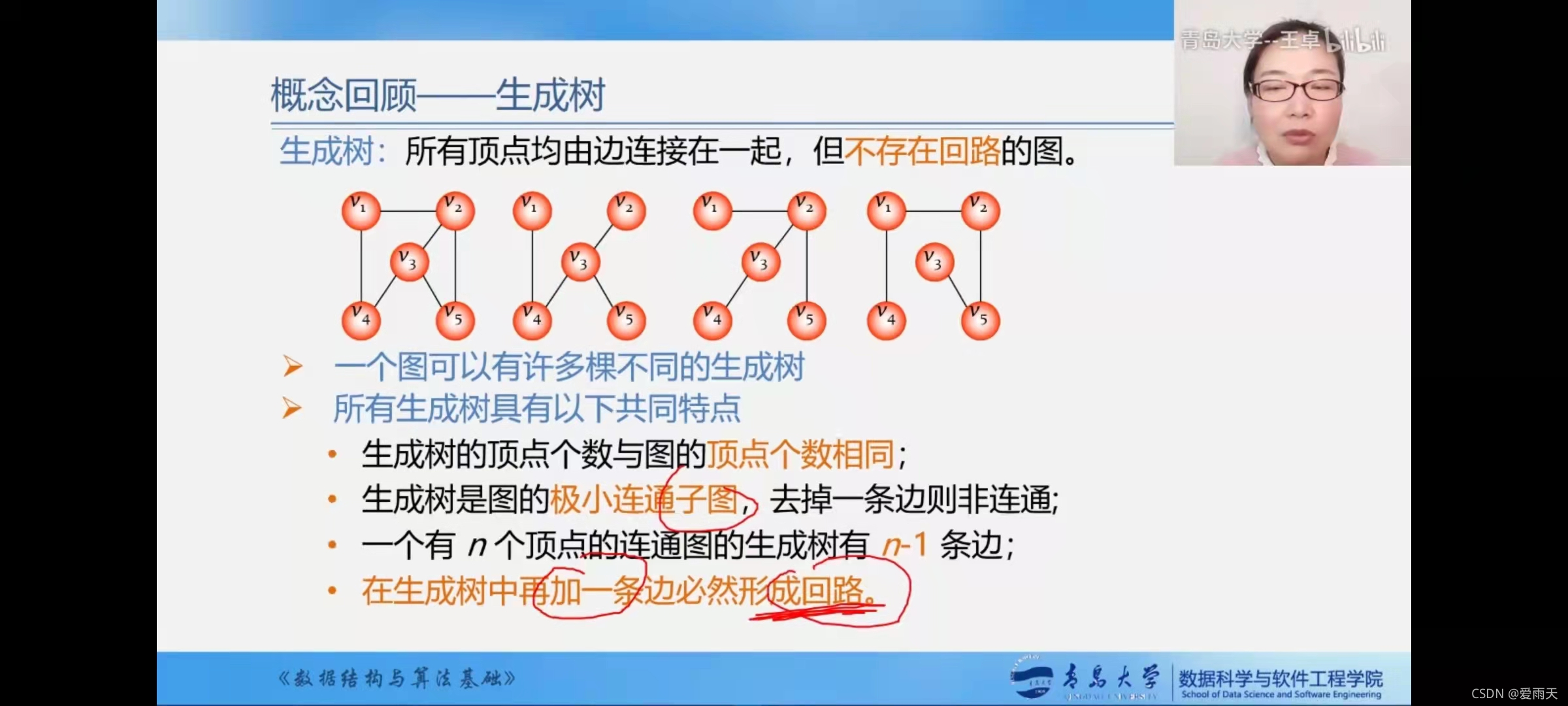
有了n个顶点和n-1条边以后，生成树中任意两个顶点间路径是唯一的

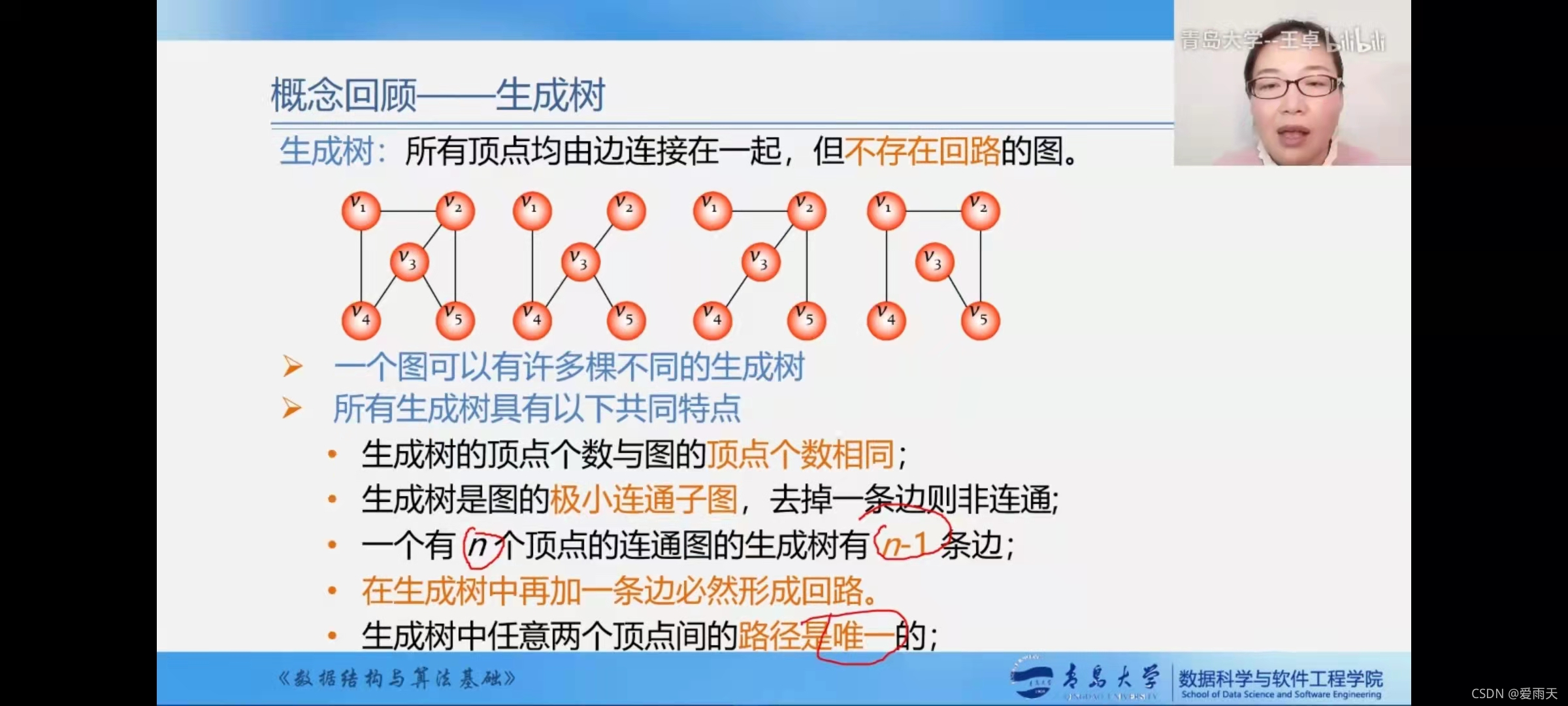
反过来，n个顶点n-1条边是不是一定是生成树呢？

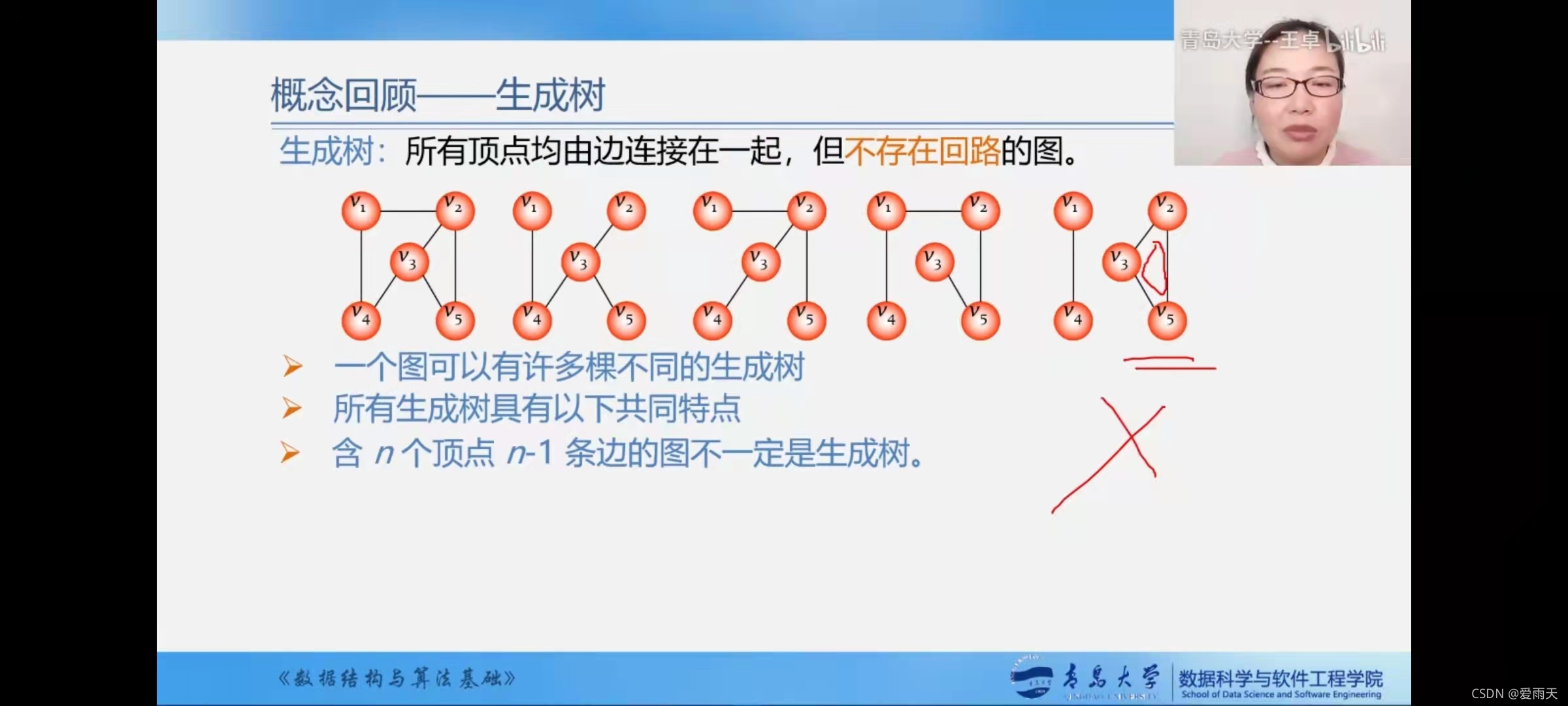
不一定

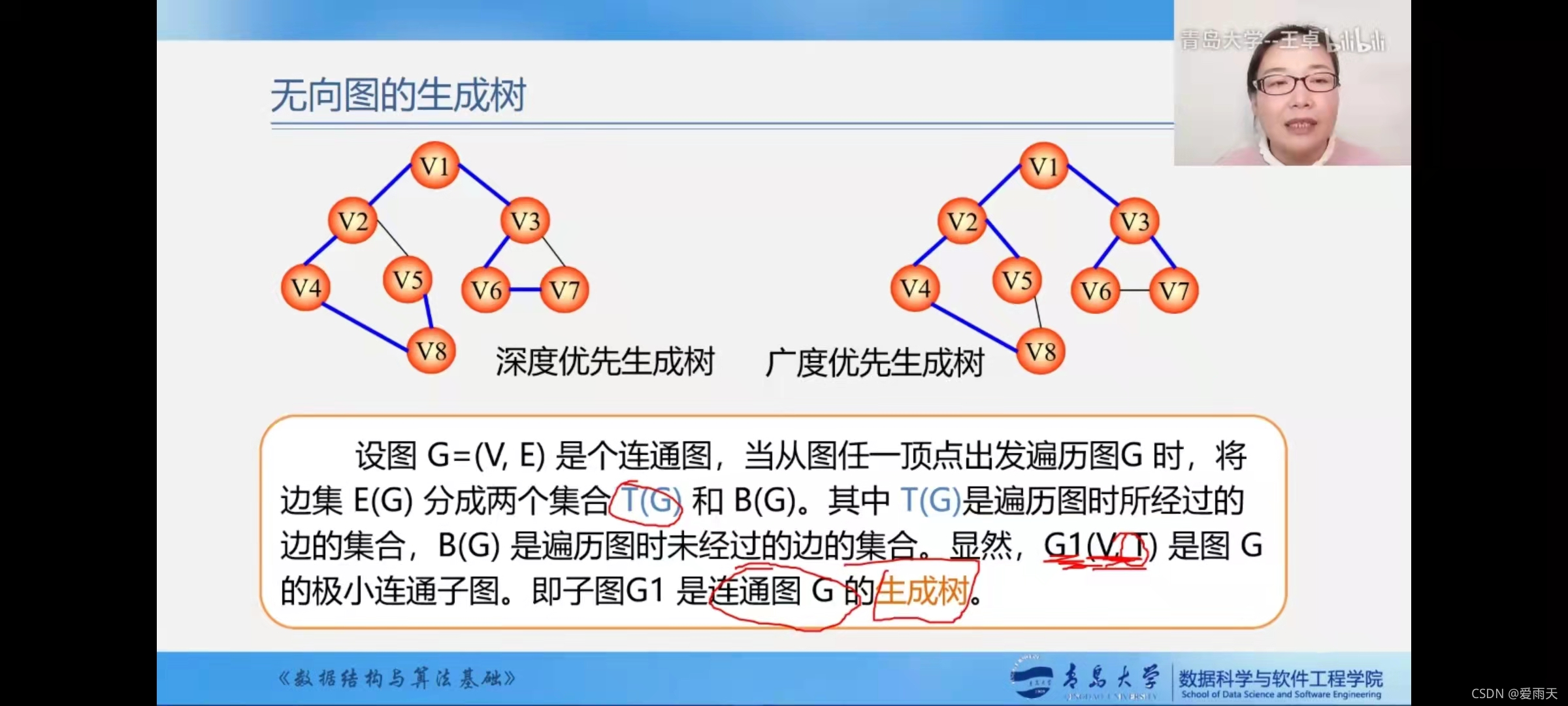
生成树怎么生成？看看无向图的生成树

最简单的方法：遍历图所有顶点，在访问的过程中把走过的边加到生成树上。

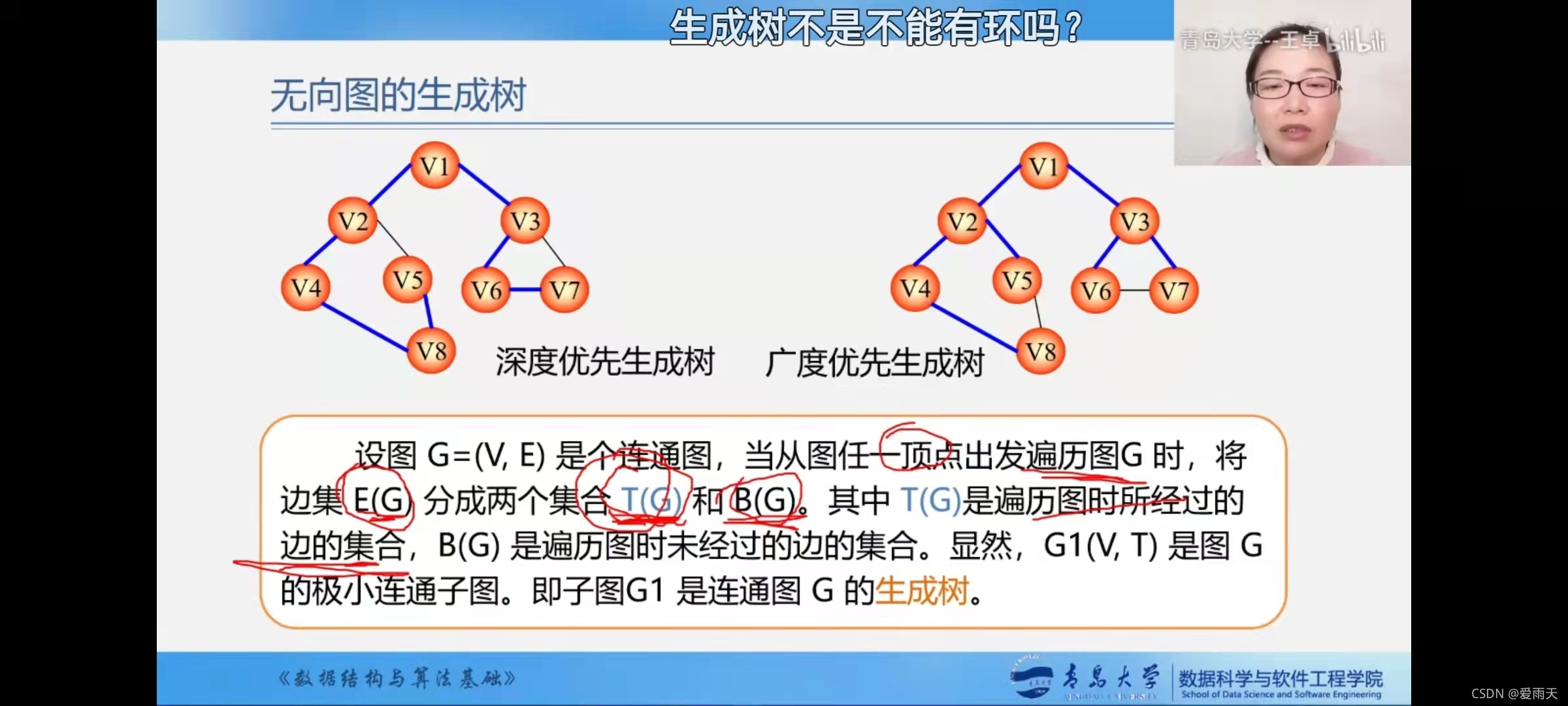
分经过的边和没经过的边

这里有个无向网，每条边上都有权值，这里构造了两个生成树，不同生成树的权值和是不一样的

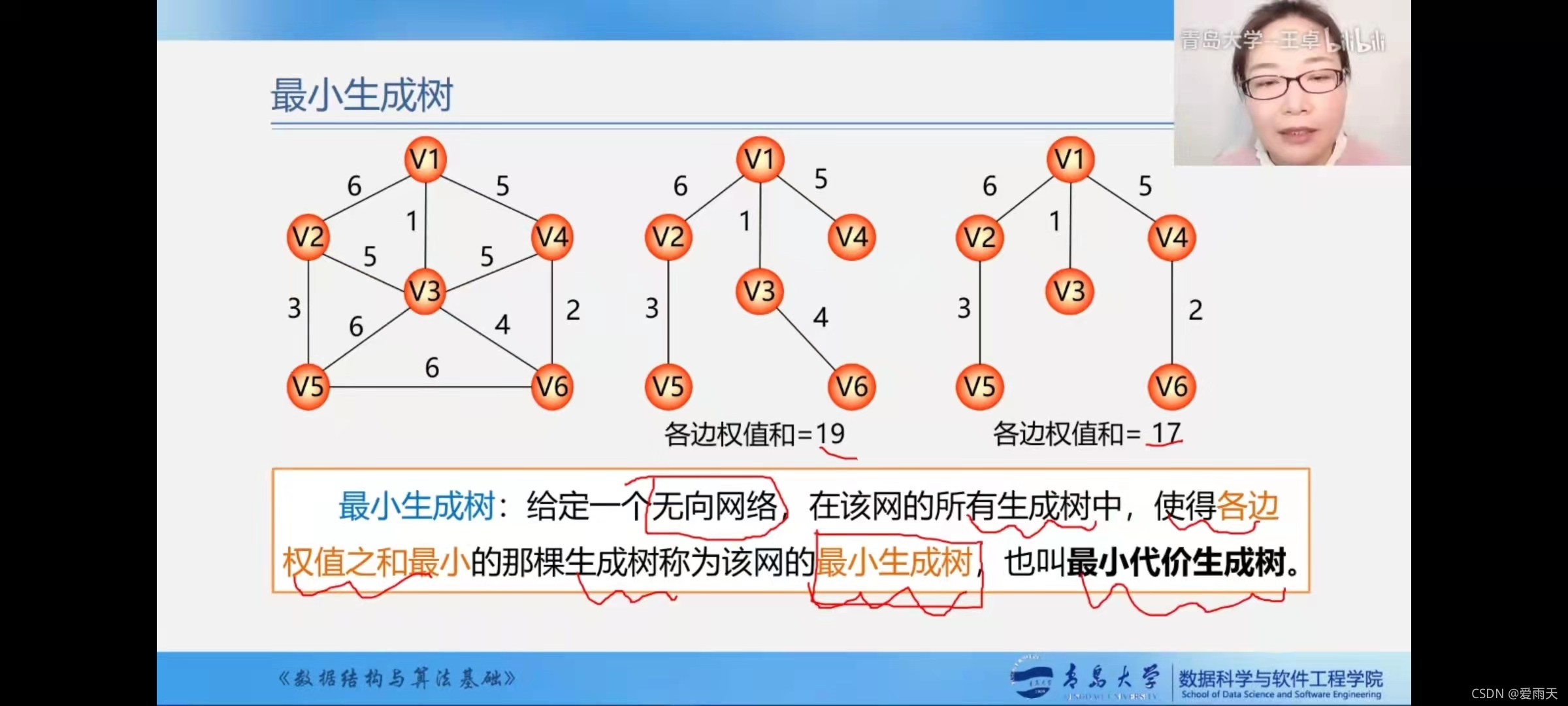
最小生成树：要求各边的权值和最小。即：我们将这些顶点连接起来，我们需要的边的权值最小

典型应用：抽象成无向网