Task05：树

原创已于 2022-03-02 17:33:54 修改 · 738 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

于 2022-02-28 20:31:43 首次发布

力扣基础训练营专栏收录该内容

13 篇文章

订阅专栏

本文介绍了如何实现二叉搜索树迭代器，通过中序遍历和栈的操作，提供hasNext和next方法的高效实现，同时讨论了进阶优化和常见示例。

1. 视频题目

1.1 二叉树的最大深度

1.1.1 描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

1.1.2 代码

第一种思路是自下而上地边号，也就是说叶子为1，向上则+1

还按照上面的例子演示，对于左子树，只有一个结点，9，depth是1

而对于右子树，15和7的depth都是1，20的depth是2，左右取较大再+1，为3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self,root):
        if not root:
            return 0
        # 结点为空，返回编号0
        
        leftDepth = self.dfs(root.left)
        # 继续向下探索左子树
        rightDepth = self.dfs(root.right)
        # 继续向下探索右子树
        return max(leftDepth,rightDepth)+1
        # 取左右子树中较大的编号+1
        # 即找到更大的深度再+1
    
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.dfs(root)

第二种是自上而下地编号，然后找左右子树的更大深度

遇空则返回父亲层次，也就是叶子结点层次

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self,root,parentDepth):
        if not root:
            return parentDepth
        # 如果为空就返回父节点的层次
            
        leftDepth = self.dfs(root.left, parentDepth+1)
        # parentDepth+1为当前层次，左子树向下寻找更大的层次
        rightDepth = self.dfs(root.right, parentDepth+1)
        # parentDepth+1为当前层次，右子树向下寻找更大的层次
        
        return max(leftDepth,rightDepth)
        # 返回两者当中更大的层次
    
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.dfs(root,0)

第三种思路就是层次遍历，每层+1，直到最后一层

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bfs(self,root):
        ans = 0
        queue = []
        # 维护队列
        queue.append(root)
        # 加入根节点
        while queue and queue[0]:
        # 队列非空，根节点非空
            ans += 1
            # 层次+1
            size = len(queue)
            # 本层的结点个数
            for _ in range(size):
            # 将本层节点的左右孩子加入队列
                cur = queue.pop(0)
                # 弹出当前访问的节点
                if cur.left:
                    queue.append(cur.left)
                # 左孩子加入队列
                if cur.right:
                    queue.append(cur.right)
                # 右孩子加入队列
        return ans
    
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.bfs(root)

1.1.3 总结

对于根节点要判断其是否为空，也要注意其没有左右孩子

层次遍历维护的是一个队列，每次访问到节点就将其孩子入队

1.2 将有序数组转换为二叉搜索树

1.2.1 描述

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：
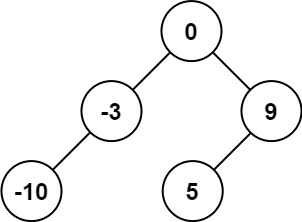
在这里插入图片描述

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

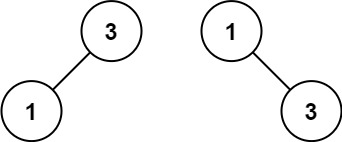
在这里插入图片描述

输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按严格递增顺序排列

1.2.2 代码

二叉搜索树意味着中序是升序，而且保证平衡，所以要从中点分开

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildBST(self, nums, low, high):
        if low > high:
            return None
            
        mid = int( low + (high-low)/2 )
        # 防止low+high后溢出，找中点都是这个操作
        
        root = TreeNode(nums[mid])
        # 中点作为根节点
        
        root.left = self.buildBST(nums, low, mid-1)
        # 更小的值放在左子树继续向下构建
        
        root.right = self.buildBST(nums, mid+1, high)
        # 更大的值放在右子树继续向下构建
        
        return root
        # 构建完毕后返回根节点
        
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        return self.buildBST(nums,0,len(nums)-1)

1.2.3 总结

二叉树相关的操作一般从递归开始考虑，每次递归只考虑最小树的情况

low + (high-low)/2，防止low+high后溢出，找中点都是这个操作

2. 作业题目

2.1 二叉树的最小深度

2.1.1 描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

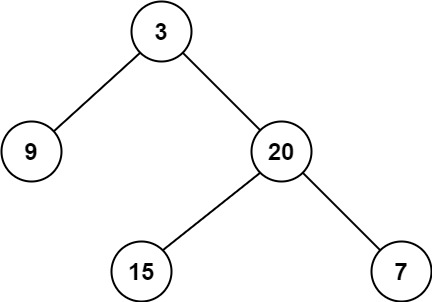
在这里插入图片描述

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

2.1.2 代码

使用广度有限搜索，自上到下层次遍历更好

遇到叶子节点直接返回深度即可，因为求的是根节点到叶子节点的路径

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bfs(self, root):
        queue = []
        # 初始化队列
        queue.append(root)
        # 根节点入队
        depth = 0
        # 初始化深度
        while queue and queue[0]:
        # 队列不空，且根节点不空
            depth += 1
            # 更新深度
            size = len(queue)
            # 本层的节点个数
            for _ in range(size):
            # 遍历本次的节点
                cur = queue.pop(0)
                # 弹出遍历到的节点
                if not(cur.left) and not(cur.right):
                    return depth
                # 如果是叶子节点就返回深度
                if cur.left:
                    queue.append(cur.left)
                # 左孩子入队
                if cur.right:
                    queue.append(cur.right)
                # 右孩子入队
        return depth
        # 根节点为空，直接返回
    def minDepth(self, root: TreeNode) -> int:
        return self.bfs(root)

我有次提交直接改了最大深度的代码，然后就报错了

其原因还是因为深度的定义，指的是从根节点到最近叶子节点

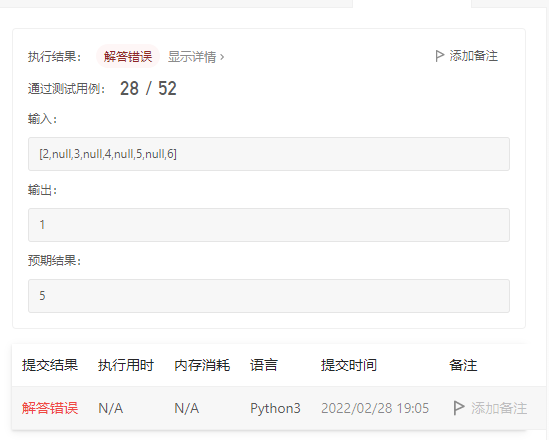
在这里插入图片描述

题中测试案例给的是这个二叉树，如下图所示

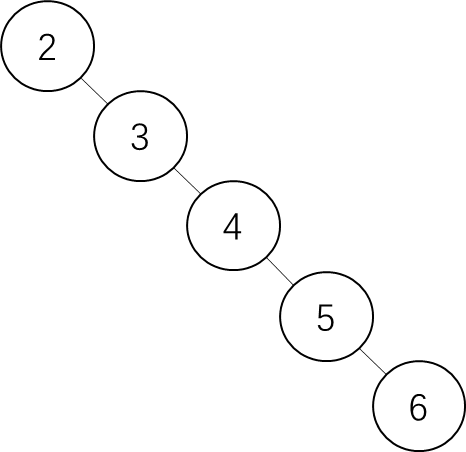
在这里插入图片描述

我们的代码如下图所示：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self,root,parentDepth):
        if not root:
            return parentDepth
        # 如果为空就返回父节点的层次
            
        leftDepth = self.dfs(root.left, parentDepth+1)
        # parentDepth+1为当前层次，左子树向下寻找更大的层次
        rightDepth = self.dfs(root.right, parentDepth+1)
        # parentDepth+1为当前层次，右子树向下寻找更大的层次
        
        return min(leftDepth,rightDepth)
        # 返回两者当中更小的层次
    
    def minDepth(self, root: Optional[TreeNode]) -> int:
        return self.dfs(root,0)

所以这个代码直接就在根节点返回了，没有到叶子节点

2.1.3 总结

一定要看清楚题目当中对相关指标的定义

2.2 路径总和

2.2.1 描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

示例 1：

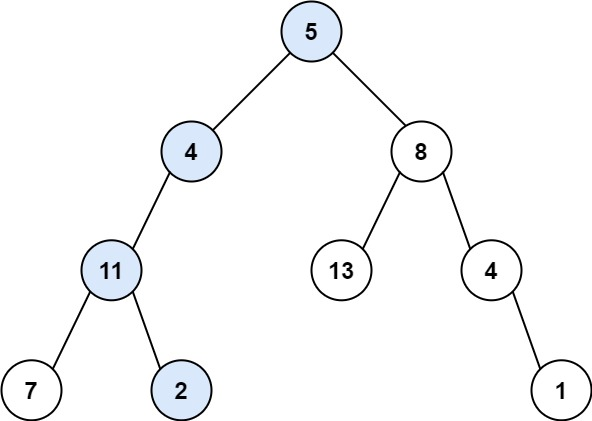
在这里插入图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

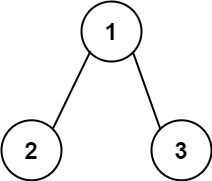
在这里插入图片描述

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

2.2.2 代码

和上一题的最小深度类似，都是需要根节点到叶子节点

那就进行层次遍历，维护两个队列，一个是节点，一个是根节点到当前节点的值

如果当前节点是叶子节点，那就判断和是否匹配，并返回相应的结果

class Solution:
    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
        if not root:
            return False
        # 遍历到空节点直接返回
        que_node = collections.deque([root])
        # 层次遍历的节点队列
        que_val = collections.deque([root.val])
        # 层次遍历的数值队列
        while que_node:
        # 节点队列不为空
            now = que_node.popleft()
            temp = que_val.popleft()
            # 取出队列头部的节点和数值
            if not now.left and not now.right:
                if temp == sum:
                    return True
                continue
            # 遍历到当前节点
            # 判断是不是叶子节点
            # 如果是叶子节点就看路径和是否匹配
            if now.left:
                que_node.append(now.left)
                # 左孩子入队
                que_val.append(now.left.val + temp)
                # 根节点到左孩子的和入队
            if now.right:
                que_node.append(now.right)
                # 右孩子入队
                que_val.append(now.right.val + temp)
                # 根节点到右孩子的和入队
            
        return False

我之前用深度优先搜索的时候报错了，对应的测试用例如下：

在这里插入图片描述

测试用例的二叉树如下图：

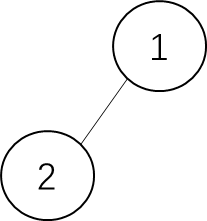
在这里插入图片描述

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def dfs(self, root, sum, targetSum):
        if not(root) :
            if sum==targetSum:
                return True
            else:
                return False
            
        leftSearch = self.dfs(root.left, root.val+sum, targetSum)
        rightSearch = self.dfs(root.right, root.val+sum, targetSum)
        
        return leftSearch or rightSearch
        
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        if not root :
            return False
        else:
            return self.dfs(root, 0, targetSum)

所以报错的原因，是把根节点当作了叶子节点，也就是没有准确判断叶子节点

2.2.3 总结

注意题中对相应指标的定义，如果临界条件是叶子节点，记得用层次遍历

2.3 二叉搜索树迭代器

2.3.1 描述

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：
BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
int next()将指针向右移动，然后返回指针处的数字。
注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：
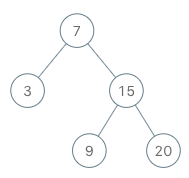
在这里插入图片描述

输入
[“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False

提示：

树中节点的数目在范围 [1, 105] 内
0 <= Node.val <= 106
最多调用 105 次 hasNext 和 next 操作

进阶：

你可以设计一个满足下述条件的解决方案吗？next() 和 hasNext() 操作均摊时间复杂度为 O(1) ，并使用 O(h) 内存。其中 h 是树的高度。

2.3.2 代码¹

看题目要求的话就是两个函数，一个是next()，另一个hasNext()

所以或许最直接最简单的操作是在初始化的时候直接中序遍历打表

class BSTIterator(object):
 
    def __init__(self, root):
        """
        :type root: TreeNode
        """
        self.res = list()
        def inorder(node):
            if not node:
                return
            
            inorder(node.left)
            self.res.append(node.val)
            inorder(node.right)
        inorder(root)
        self.index = 0
 
    def next(self):
        """
        @return the next smallest number
        :rtype: int
        """
        self.index += 1
        # print self.index - 1, self.res
        return self.res[self.index - 1]
        
 
    def hasNext(self):
        """
        @return whether we have a next smallest number
        :rtype: bool
        """
        return self.index < len(self.res)

但是这个操作似乎不那么地Iterator，如果每次之走遍历的一步可能更像

那每次遍历的子树，其左孩子一定是全局最小的，所以每次应该都是从最左的孩子开始

也就是说，递归遍历，一直压左孩子入栈，直到叶子节点

然后每次访问的时候，弹出当前节点的值，然后压右孩子的左孩子的左孩子…到叶子节点

所以说，全局的时候是从最左的孩子开始的，下一步压入的右孩子是空

所以栈顶元素是最左的孩子的父节点，即向上一层，然后再压父节点的右孩子的左孩子的左孩子…到叶子节点

class BSTIterator(object):
 
    def __init__(self, root):
        """
        :type root: TreeNode
        """
        self.stack = []
        self.pushLeft(root)
 
    def next(self):
        """
        @return the next smallest number
        :rtype: int
        """
        popedNode = self.stack.pop()
        self.pushLeft(popedNode.right)
        return popedNode.val
 
    def hasNext(self):
        """
        @return whether we have a next smallest number
        :rtype: bool
        """
        return len(self.stack) != 0
    
    def pushLeft(self, node):
        while(node):
            self.stack.append(node)
            node = node.left