[牛客算法总结]：二叉树的直径

最新推荐文章于 2025-07-03 09:45:53 发布

Blue Protocol

最新推荐文章于 2025-07-03 09:45:53 发布

阅读量417

点赞数

CC 4.0 BY-SA版权

分类专栏：牛客算法文章标签： java 算法

本文链接：https://blog.youkuaiyun.com/weixin_51921447/article/details/126634587

牛客算法专栏收录该内容

40 篇文章

订阅专栏

本文介绍了如何使用递归算法解决二叉树的最大直径问题。在给定的二叉树中，直径定义为任意两个节点之间的最长路径。通过分析三种可能的直径情况（以根节点、左子节点、右子节点为起点），并计算左右子树的高度，可以找到最大直径。代码示例展示了如何实现这一算法，适用于节点数量不超过100的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：

给定一颗二叉树，求二叉树的直径。
1.该题的直径定义为：树上任意两个节点路径长度的最大值
2.该题路径长度定义为：不需要从根节点开始，也不需要在叶子节点结束，也不需要必须从父节点到子节点，一个节点到底另外一个节点走的边的数目
3.这个路径可能穿过根节点，也可能不穿过
4.树为空时，返回 0
如，输入{1,2,3,#,#,4,5}，二叉树如下:
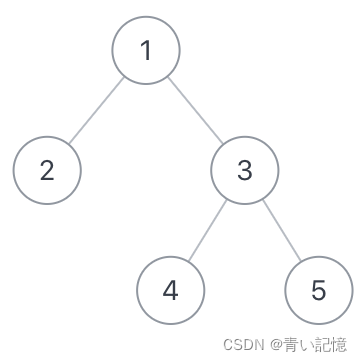
请添加图片描述
那么：
从4到5的路径为4=>3=>5，路径长度为2
从4到2的路径为4=>3=>1=>2，路径长度为3

如，输入{1,2,3,#,#,4,5,9,#,#,6,#,7,#,8}，二叉树如下:
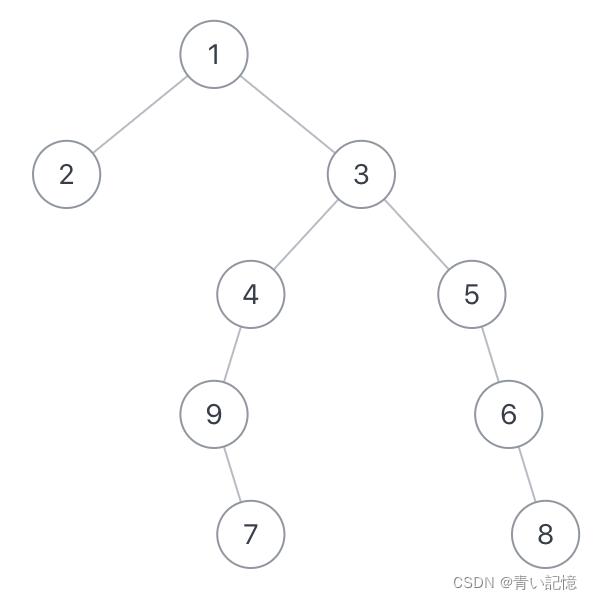
请添加图片描述
那么路径长度最长为:7=>9=>4=>3=>5=>6=>8，长度为6

数据范围：节点数量满足0≤n≤100

反思：

这个题目自己在看题的时候被条件给看懵了，没有想到二叉树的最大直径如果以当前头节点为树，直径就是左右两颗子树的高度的相加。
因为是二叉树，所以有三种情况：
1、以root为头节点，直径为左右两个子树高度的相加。
2、以root.left为头节点，直径同上。
3、以root.right为头节点，直径同上。
然后取这三者的最大值即可。

用到的知识点：

数、递归

代码：

    public int  getTreeHeight(TreeNode root)  {
        if (root == null) {
            return 0;
        }
        int lHeight = getTreeHeight(root.left);
        int rHeight = getTreeHeight(root.right);
        return lHeight > rHeight ? lHeight + 1 : rHeight + 1;
    }

    public int diameterOfBinaryTree (TreeNode root) {
        // write code here
        if (root == null) {
            return 0;
        }
        int leftHeight = getTreeHeight(root.left);
        int rightHeight = getTreeHeight(root.right);
        int nowTreeHeight =  leftHeight + rightHeight;
        int leftTreeDiameterOfHeight = diameterOfBinaryTree(root.left);
        int rightTreeDiameterOfHeight = diameterOfBinaryTree(root.right);
        return nowTreeHeight >  leftTreeDiameterOfHeight ? nowTreeHeight :
               leftTreeDiameterOfHeight > rightTreeDiameterOfHeight ?
               leftTreeDiameterOfHeight : rightTreeDiameterOfHeight;
    }