最短路径时图论中典型的问题,可用于路线规划等问题。求任意两点之间的最短路径可使用Floyd算法。
算法步骤
如果要让任意两点之间的路程变短,引入第三个点,也可引入多个点,也可能缩短原本两个点的距离:
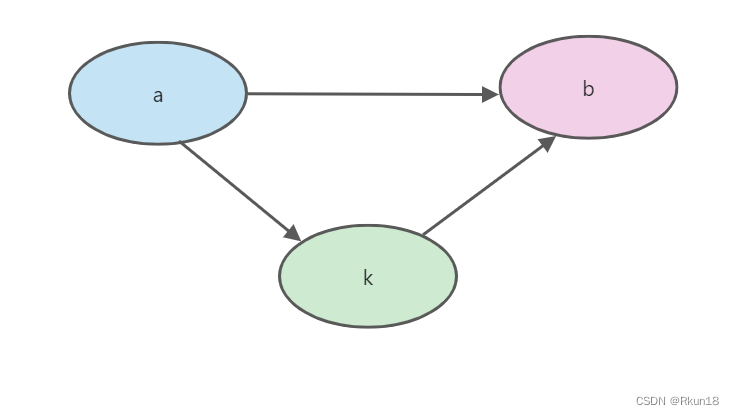
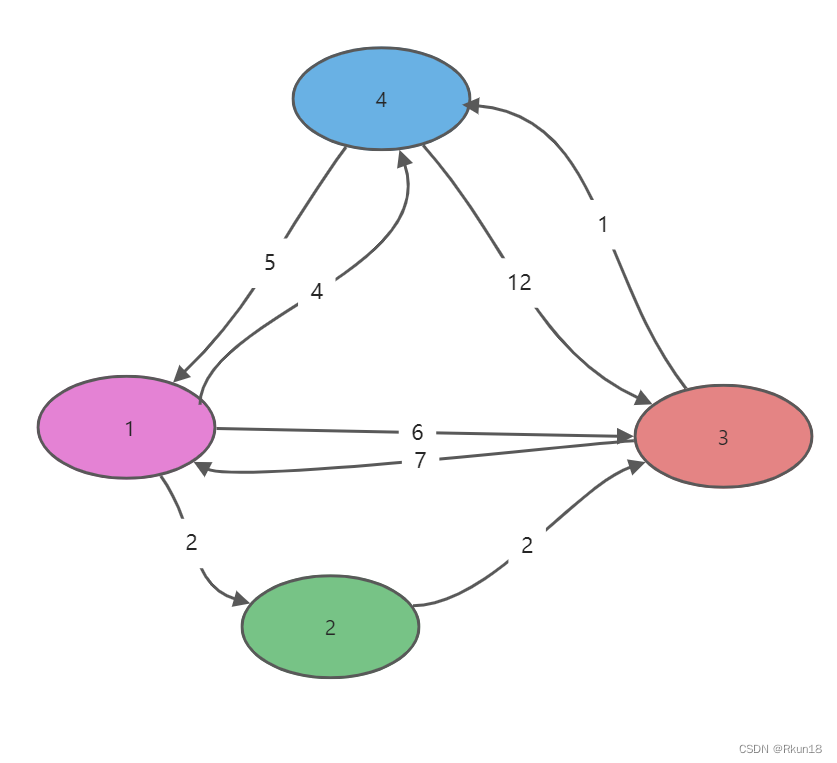
如上图的4号城市到3号城市,原本路程是a[4][3]=12,如果通过1号城市4->1->3路程将缩短为a[4][1]
+a[1][3]=5+6=11。如果同时通过1号和2号中转,4号到3号的距离又会缩短
为a[4][1]+a[1][2]+a[2][3]=10。综上,我们发现每个点都可能使另外两个顶点之间路程变短。我们可以通过递推模拟该过程。
首先存储这个图,使用二维数组存储:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 2 | 6 | 4 |
| 2 | ∞ | 0 | 3 | ∞ |
| 3 | 7 | ∞ | 0 | 1 |
| 4 | 5 | ∞ | 11 | 0 |

假设只允许经过1号顶点中转,求任意两点的最短路径(i到j):
只需判断a[i][1]+a[1][j]是否比a[i][j]小。代码:
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(a[i][j]>a[i][1]+a[1][j])
a[i][j]=a[i][1]+a[1][j];
}
再经过2号点中转:
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(a[i][j]>a[i][2]+a[2][j])
a[i][j]=a[i][2]+a[2][j];
}
然后逐个点中转。
简写为:
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
}
总结
Floyd算法可以算出任意两点的最短路径,可以处理有负边,但不能处理负环。负环是指累加起来为负数。
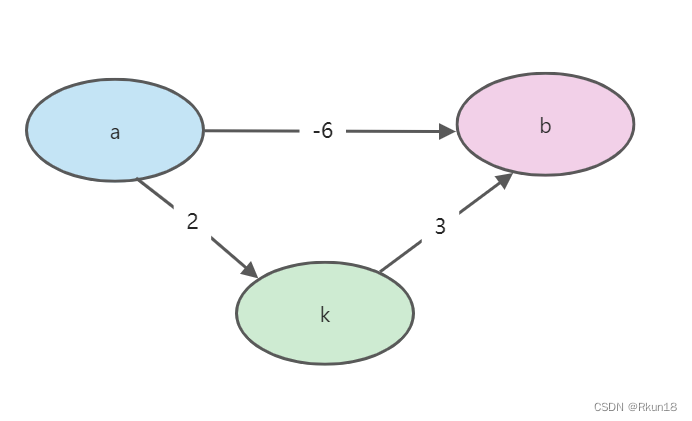
 Floyd算法详解:计算图中任意两点最短路径
Floyd算法详解:计算图中任意两点最短路径





 Floyd算法是一种用于查找图中所有顶点对间最短路径的动态规划方法。该算法通过迭代的方式,考虑每个顶点作为中转站,逐步更新最短路径。在可能存在负权边但无负权环的图中,Floyd算法能有效找到最短路径。其核心思想是通过两层循环检查每一对顶点,通过第三个顶点作为中介是否能缩短路径,并更新距离矩阵。最终得到的矩阵即包含了所有顶点对的最短路径信息。
Floyd算法是一种用于查找图中所有顶点对间最短路径的动态规划方法。该算法通过迭代的方式,考虑每个顶点作为中转站,逐步更新最短路径。在可能存在负权边但无负权环的图中,Floyd算法能有效找到最短路径。其核心思想是通过两层循环检查每一对顶点,通过第三个顶点作为中介是否能缩短路径,并更新距离矩阵。最终得到的矩阵即包含了所有顶点对的最短路径信息。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








