一、创新点
1 时空注意力机制
提取空间注意力时,要考虑到不同时间片内各个节点是怎样相互影响的。
提取时间注意力时,要考虑到各个节点的交通流量在不同时间片下的变化。
1.1 空间注意力
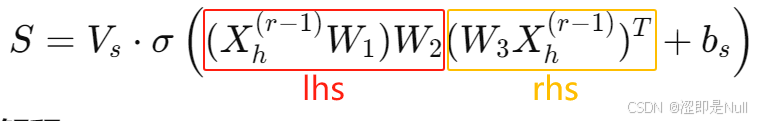
式中,X为输入数据,维度为(节点数N × 特征数C × 时间序列长度T)。W1是负责对X的时间维度进行变换的权重矩阵,W3是对X的特征维度的数据进行处理的权重矩阵,W2是用来结合时间维度和特征维度信息的权重矩阵。
与经典的注意力机制对比,左边的 lhs 类似于 Query,右边的 rhs 类似于 Key(并不是完全等价),两者相乘的结果设为 product,相当于注意力分数。
lhs = nd.dot(nd.dot(x, self.W_1.data()), self.W_2.data())
rhs = nd.dot(self.W_3.data(), x.transpose((2, 0, 3, 1)))
product = nd.batch_dot(lhs, rhs)
S = nd.dot(self.V_s.data(), nd.sigmoid(product + self.b_s.data()).transpose((1, 2, 0))).transpose((2, 0, 1))得到注意力矩阵 S 后,还需要把注意力分数通过 softmax 转化为空间注意力矩阵。
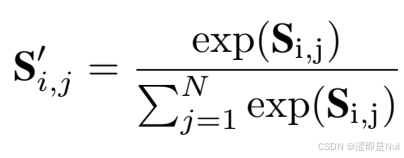
S = S - nd.max(S, axis=1, keepdims=True) # 避免计算exp时数值溢出
exp = nd.exp(S)
S_normalized = exp / nd.sum(exp, axis=1, keepdims=True)1.2 时间注意力
计算时间注意力与空间注意力的思想相同,
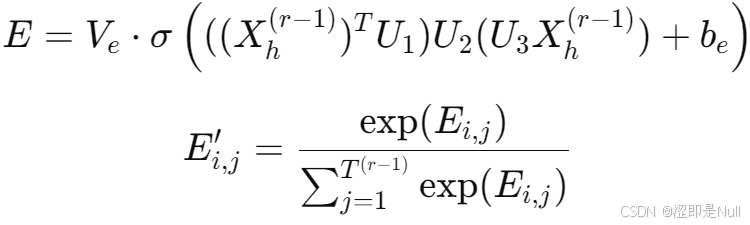
U1 用来提取每个时间片中的节点相关信息,U3 用来提取输入数据的特征维度信息,U2用来综合考虑特征维度和节点相关性。
2 时空卷积模块
2.1 空间维度上的图卷积
空间图卷积使用的方法与论文《STGCN》中提到的大差不差。包括拉普拉斯矩阵的谱分解、图信号的傅里叶变换、切比雪夫多项式递归定义。
那么真正的创新点在于图卷积和空间注意力的融合。对每一项切比雪夫多项式 Tk(L),使其与空间注意力矩阵 S' 进行对应元素乘积(哈达玛积)。最终图卷积公式变为:

具体的代码如下,其中 graph_signal 为每一个时间步下的输入x,也就是输入x去掉最后一个时间步长维度,因此它的形状为(批次大小,顶点数量,特征数) 。
for k in range(self.K):
T_k = self.cheb_polynomials[k]
T_k_with_at = T_k * spatial_attention # 计算哈达玛积
theta_k = self.Theta.data()[k]
rhs = nd.batch_dot(T_k_with_at.transpose((0, 2, 1)), graph_signal)
output = output + nd.dot(rhs, theta_k)2.2 时间维度的标准卷积
在得到时间注意力矩阵 E' 后,将其直接应用于输入数据后可得,
![]()
x_TAt = nd.batch_dot(x.reshape(batch_size, -1, num_of_timesteps), temporal_At).reshape(batch_size, num_of_vertices, num_of_features, num_of_timesteps)然后通过空间图卷积(gθ * G)、时间维度上的标准卷积(Φ∗)、非线性激活(ReLU)后可以得到第 r 层的近期模块。

虽然作者在这里并没有提及 Xh(r-1) 是否就是前面时间注意力提到的 Xh(r-1),但是从代码可以看出,作者对上面得到的 x_TAt (前面时间注意力提到的 Xh(r-1))直接添加了空间注意力。所以个人认为这个公式的 Xh(r-1) 既包含时间注意力,又包含空间注意力。
spatial_At = self.SAt(x_TAt) # 空间注意力
spatial_gcn = self.cheb_conv_SAt(x, spatial_At) # 空间图卷积
# 时间维度上的标准卷积
time_conv_output = (self.time_conv(spatial_gcn.transpose((0, 2, 1, 3))).transpose((0, 2, 1, 3)))
# 残差连接
x_residual = (self.residual_conv(x.transpose((0, 2, 1, 3))).transpose((0, 2, 1, 3)))
# 非线性激活+层归一化
return self.ln(nd.relu(x_residual + time_conv_output))二、模型结构
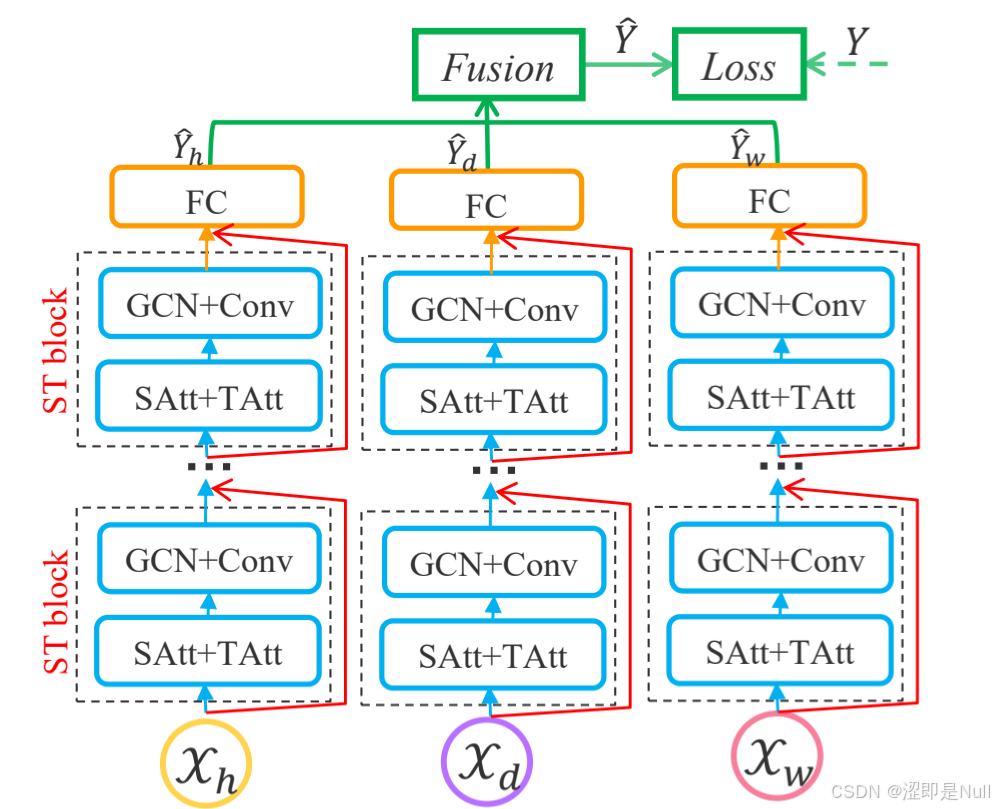
这个图再结合代码,可以看出,ASTGCN 一共分为三列,每一列都是一个子模型(ASTGCN_submodule),代表着近期片段(Xh)、日周期片段(Xd)、周周期片段(Xw)。每一个子模型都分为好几个时空卷积块 ASTGCN_block(代码中有两个 backbone,也就是两个时空卷积块)。每一个时空卷积块内就是第一部分讲到的两个创新点。
在得到不同子模型的预测结果 ŷ 后,需要使用多模块融合机制对三个子模型作出不同的加权计算,最终得到总的 ŷ。
![]()
三、实验
1 删除过多的检测器
作者采用了 PeMSD4 和 PeMSD8 两个数据集验证模型。但是考虑到这两个数据集中存在相邻检测器之间的距离过短,也就是检测器之间过于密集的情况。这样不仅会增加计算成本,而且太多的微观数据会降低模型学习效率。因此作者修改了那两个数据集,删除了距离大于3.5英里的相邻检测器。最终,PeMSD4 数据集保留了307个(原3848个)检测器,PeMSD8 数据集保留了170个(原1979个)检测器。
2 空间注意力案例
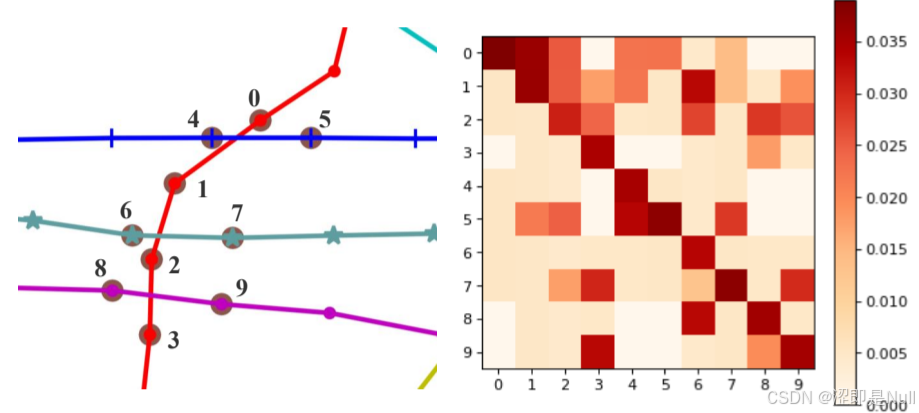
从上图左可以看出,9号检测器和3号、8号检测器的交通流相关性较强。再看右图最后一列,也是3号、8号的颜色较深。
























 1347
1347

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








