LeetCode刷题第十六天（153. 寻找旋转排序数组中的最小值）

---

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

1. 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
2. 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

算法思想

一个不包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：
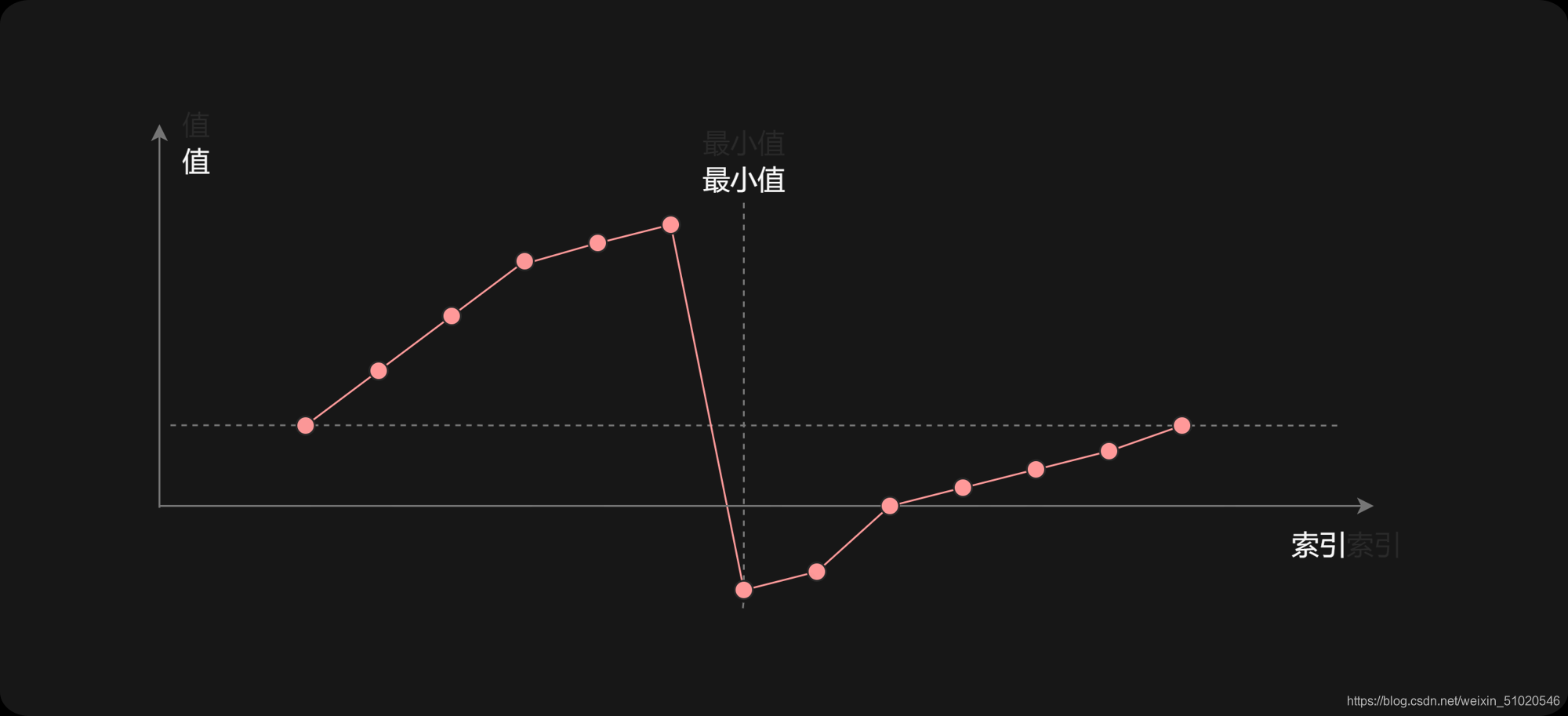其中横轴表示数组元素的下标，纵轴表示数组元素的值。图中标出了最小值的位置，是我们需要查找的目标。

我们考虑数组中的最后一个元素 $x$：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 $x$；而在最小值左侧的元素，它们的值一定都严格大于 $x$。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 $low$，右边界为 $high$，区间的中点为 $pivot$ ，最小值就在该区间内。我们将中轴元素 $nums[pivot]$ 与右边界元素 $nums[high]$ 进行比较，可能会有以下的三种情况：

第一种情况是 $nums[pivot]<nums[high]$。如下图所示，这说明 $nums[pivot]$ 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

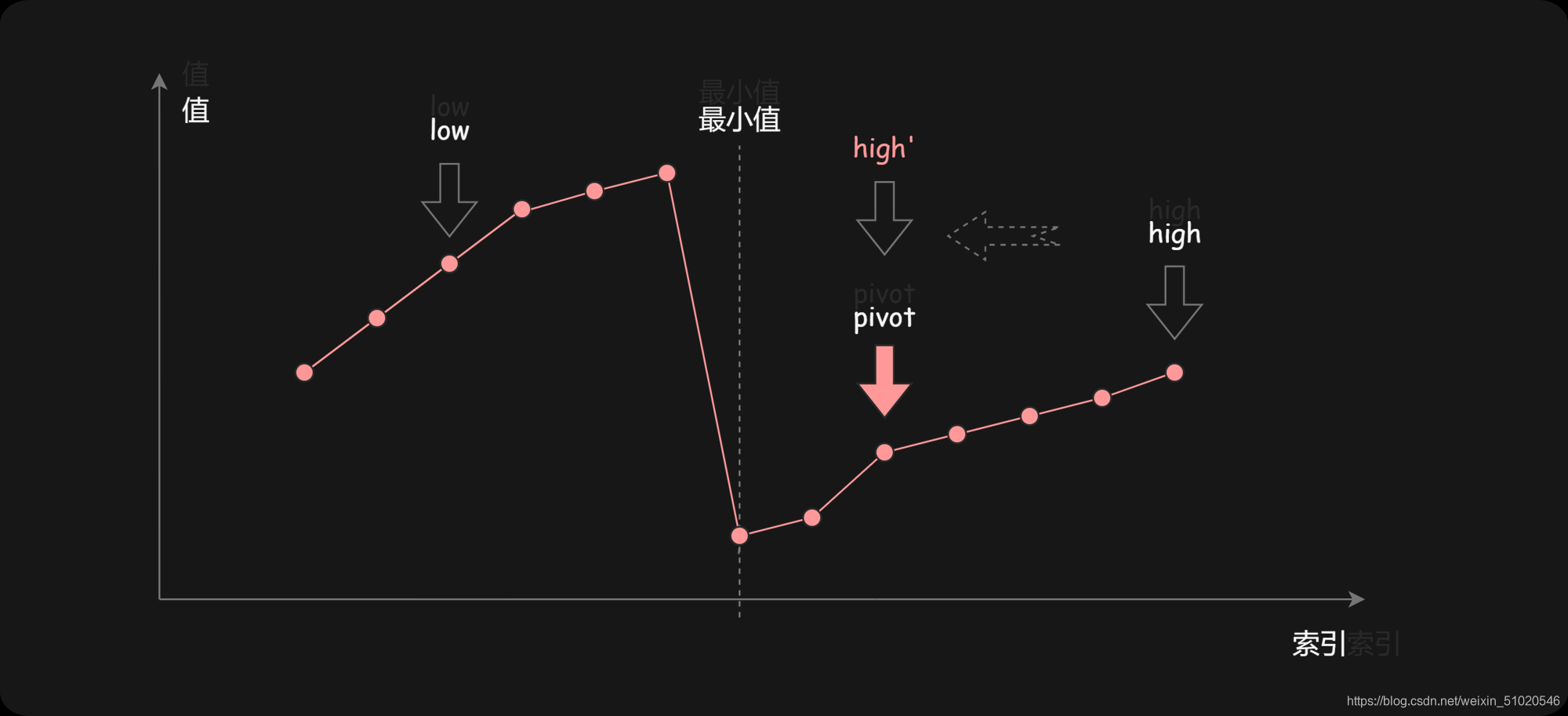第二种情况是 $nums[pivot]>nums[high]$。如下图所示，这说明 $nums[pivot]$ 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

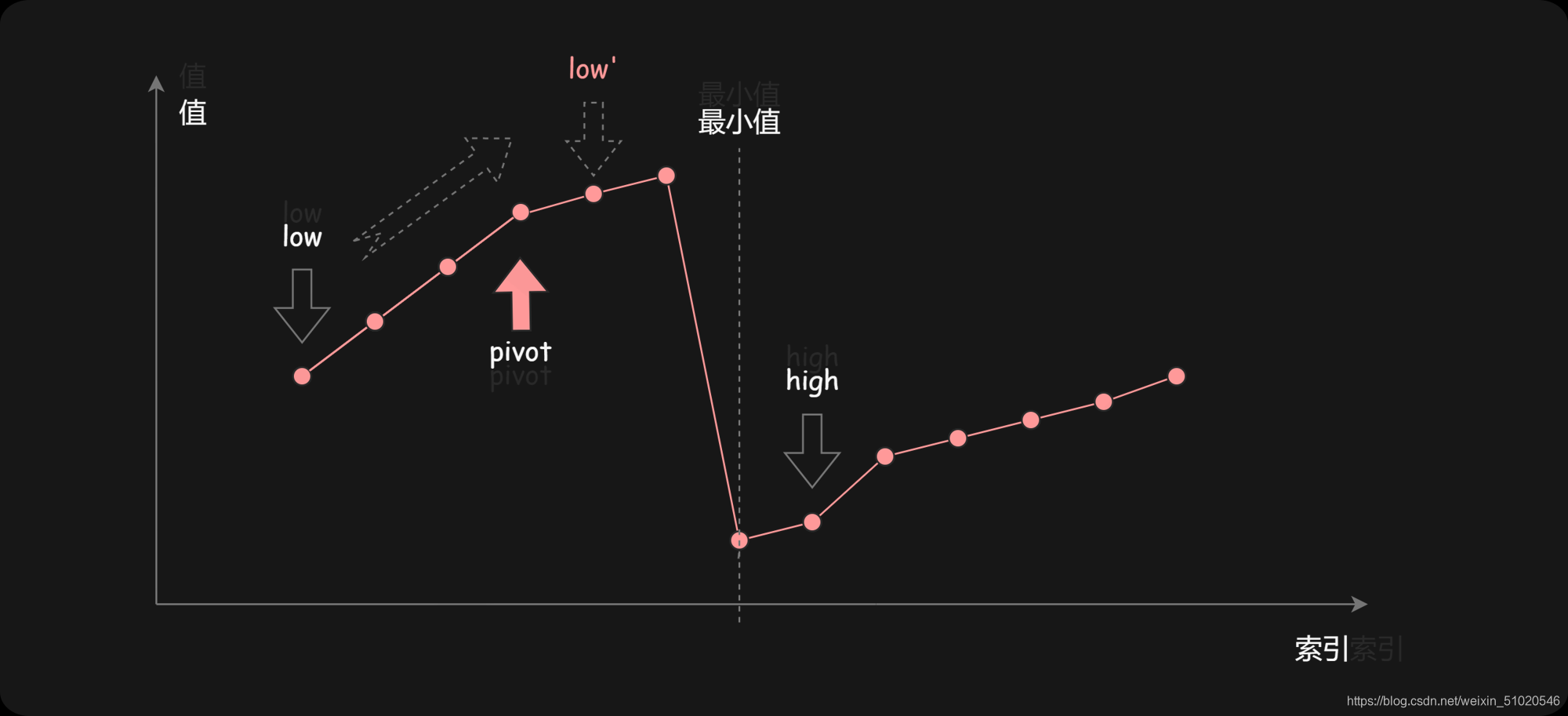
由于数组不包含重复元素，并且只要当前的区间长度不为 $1$，$pivot$ 就不会与 $high$ 重合；而如果当前的区间长度为 $1$，这说明我们已经可以结束二分查找了。因此不会存在 $nums[pivot]=nums[high]$ 的情况。

当二分查找结束时，我们就得到了最小值所在的位置。

JAVA代码

class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            } else {
                low = pivot + 1;
            }
        }
        return nums[low];
    }
}

或者：

class Solution {
    public int findMin(int[] nums) {
        if (nums.length==1){
            return nums[0];
        }
        if (nums.length==0){
            return -1111;//这块需要报错返回异常。。。数组输入为空！
        }
        int left=0;
        int right = nums.length-1;
        int mid;
    
        while(left<right){
            mid=left+(right-left)/2;
            if(nums[mid]<nums[right]){
                right=mid;
            }else{
                left=mid+1;
            }
        }
        return nums[left];
    }
}

复杂度

1. 时间复杂度：时间复杂度为 $O(logn)$，其中 $n$ 是数组 $nums$
   的长度。在二分查找的过程中，每一步会忽略一半的区间，因此时间复杂度为 $O(logn)$。
2. 空间复杂度：$O(1)$。

链接：https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/solution/xun-zhao-xuan-zhuan-pai-xu-shu-zu-zhong-5irwp/
来源：力扣（LeetCode）