装载问题（背包问题思想的运用）

1.问题
有两艘船，载重量分别是c1、c2，n个集装箱，重量是wi（i=1,2,…,n），且所有的集装箱的总重量不超过c1+c2。问是否有合适的装载方案，将n个集装箱放到这两艘轮船上，若有则找出方案。

2.解析
算法思路：将第一艘船尽量装满（第一艘船放的集装箱的重量之和接近c1），剩余的集装箱放入第二艘船，若剩余的集装箱重量之和大于第二艘船的载重量c2，则无解。

解决此问题时联系之前学过的0-1背包问题，0-1背包问题最重要的思想是：

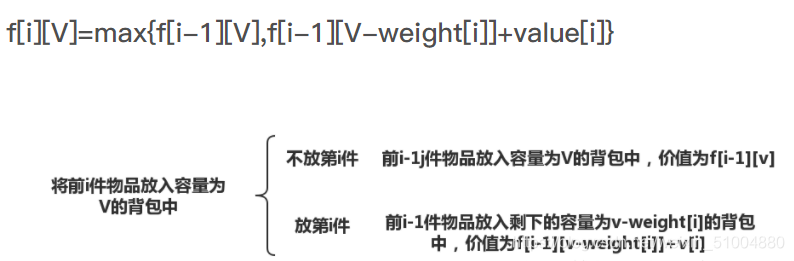
这个式子可以推广到其他问题的应用，比如上述装载问题。
其实质是求一堆数在一定范围限制中能取得的和的最大值。

所以在考虑装载问题时，可以先把问题简化成只考虑一艘船，即这些集装箱的重量在不超过c1范围内能取得的和的最大值。这个最大值可以用0-1背包问题的思想求得，然后检查剩下的集装箱的重量的和与c2的关系，若大于c2说明此问题无解，若不超过c2则说明存在最优装载方案。

假设问题的解是<x1,x2,…,xn>，其中xi=0。如果xi=1，那么第i项任务放到第一台机器加工，如果xi=0,那么第i项任务放到第二台机器加工。把这个问题描述成组合优化问题：
目标函数：
max x1t1+x2t2+…+xntn
约束条件：
x1t1+x2t2+…+xntn<=c1
xi=0或者1,i=1,2,3,…,n

3.设计

核心伪代码：
int zhuangzai(int c1,int c2,int n,int w[]){
   
   
	int sum=0,sum1=0,sum2=0;
	
	//初始化，f[i][0]表示载重量c1=0时轮船的最大重量，f[0][j]表示载重量为c1的轮船不装任何集装箱时的最大重量 
    for(int i=0;i<=n;i++){
   
   
    	f[i][0]=0;
	}
    for(int j=0;j<=c1;j++){
   
   
    	f[0][j]=0;
	}
    
	printf("集装箱的编号 集装箱的重量\n");	    
    for(int i=1;i<=n;i++){
   
   
		printf("%7d      %7d",i,w[i]);
        for(int j=1;j<=c1;j++){
   
   
            if(j<w[i]){
   
   //集装箱的重量比载重量为c1的轮船剩余的载重量大，说明无法继续装下下一个集装箱，此时的f与前i-1个的f是一样的  
				f[i][j]=f[i-1][j];
			}
            else{
   
   //集装箱的重量不超过载重量为c1的轮船剩余的载重量，说明此时可以装下下一个集装箱，但是装了也不一定能达到最优解，所以在装与不装之间选择最优的一个 
                f[i][j]=max(f[i-1][j],f[i-1