应用密码学期末速通复习

模运算

分数求模

# 一个例子
1/2 mod 23
n ≡ 1/2 mod 23
2n ≡ 1 mod 23
# 也就是求2的逆元了
n = 12

负数求模

# 一个例子	x mod y ≡ x-y* |⎣x/y⎦|
# 后面的是 x/y并且向下取整
-73 mod 23 ≡ -73 - 23 * ⎣-73/23⎦
					 = -73 - 23 * ⎣-3.17⎦
					 = -73 - 23 * -4
					 = -73 + 92
					 = 19

gcd最大公约数

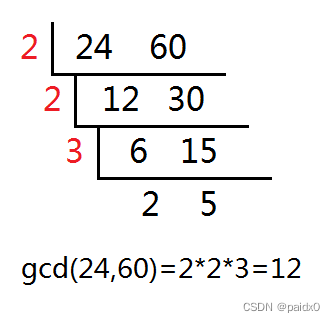
逆元

# 辗转相除
除数作为被除数、余数作为除数
一直循环除，直到除数为 0
逆元 = 余数不为0的商相乘 + 除数为0的被除数(也就是gcd)

分组密码

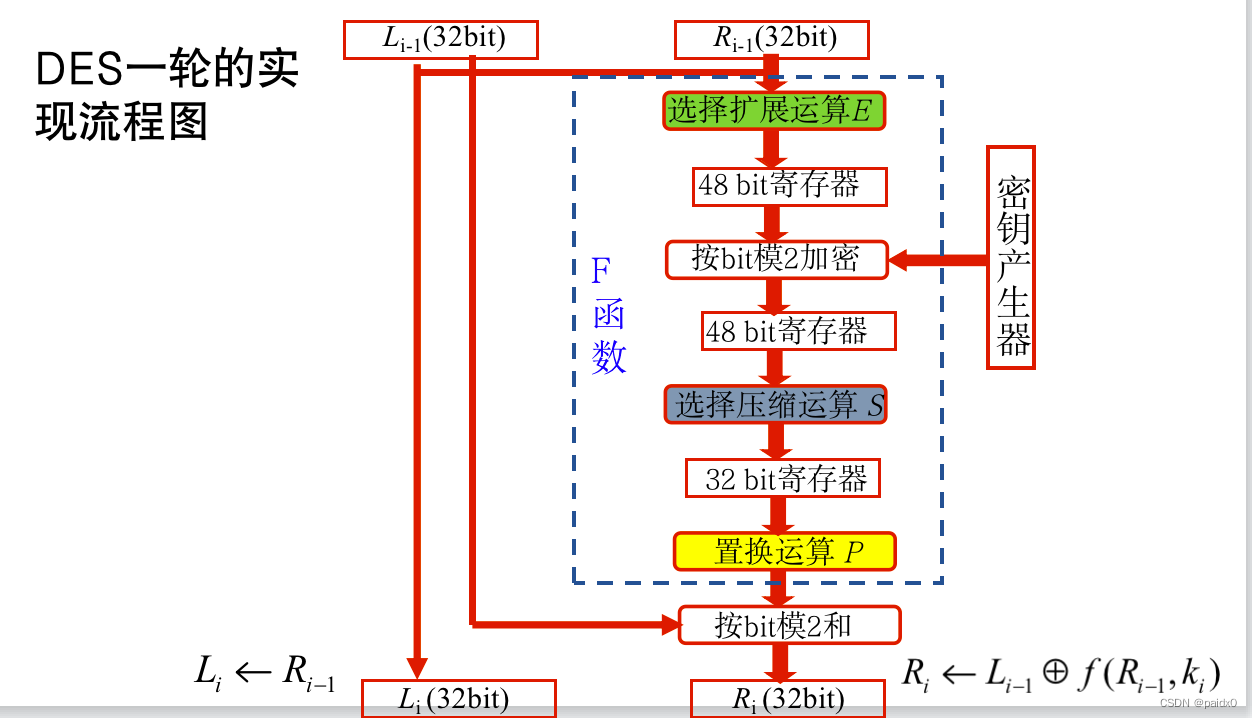
DES加密

# 分组长度64位，64位秘钥（8位校验位）,16轮迭代，每轮子密钥48位
# Feistel网络

# 加密
Li = Ri-1
Ri = Li-1⨁F(ki,Ri-1)
# 解密
Ri-1 = Li
Li-1 = Ri⨁F(ki,Li)

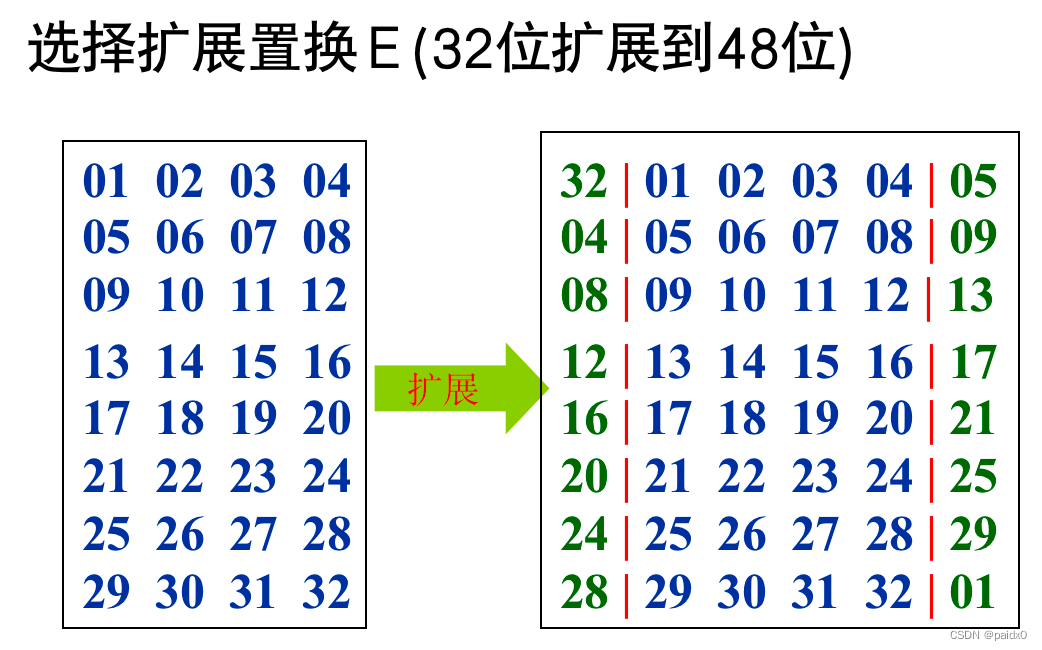
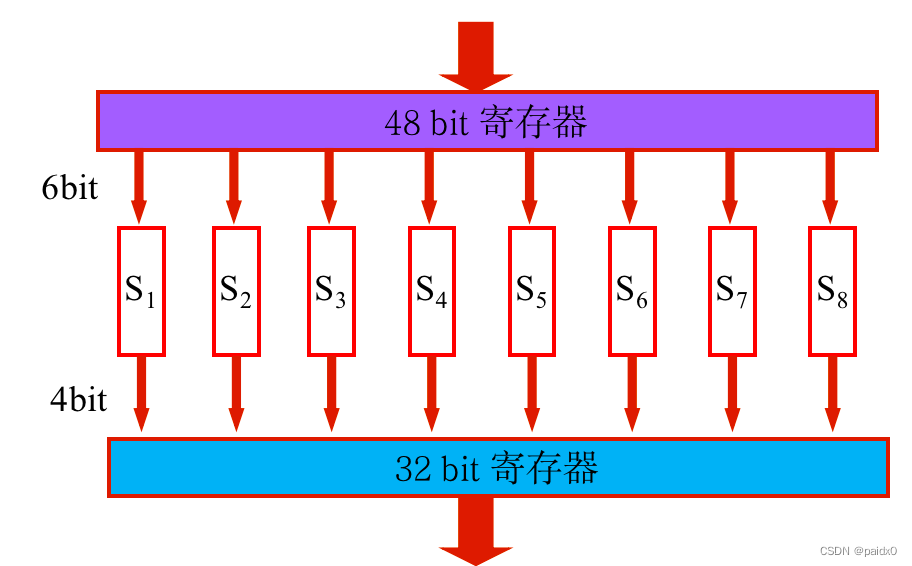
# S盒 4行16列，每行都是打乱顺序的0~15，48位8组，每组6位
# 100011，首尾代表行11(3)，中间代表列0001(1)，所以置换成第3行1列的数字，也就是6位压缩成4位

AES加密

........

操作模式

• ECB最快最简单，安全性最弱，通常加密随机数据

• CBC适合文件、软件加密，少量错误不会造成同步失败

• CFB加密字符序列，具有同步恢复

• OFB极易出错的环境使用，需要严格高速的同步机制

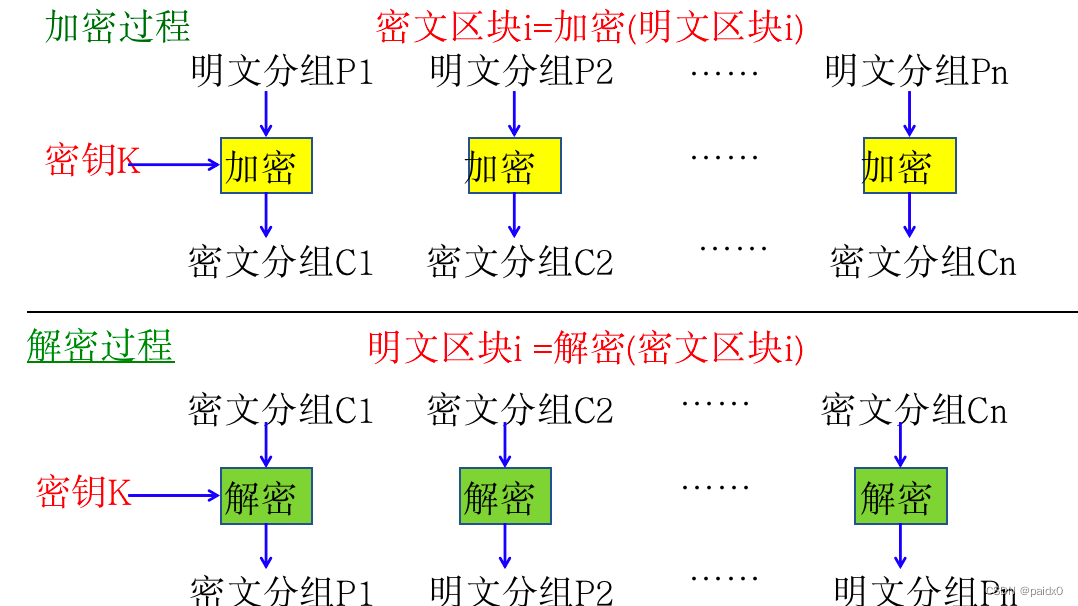
ECB电子密码本

简单，主要内容较短且随机的报文传递
加密独立分组，可以并行
单个分组的比特错误不会传播其他分组
# 相同明文或秘钥得到相同的密文，明文中重复的内容在密文体现出来，容易被统计

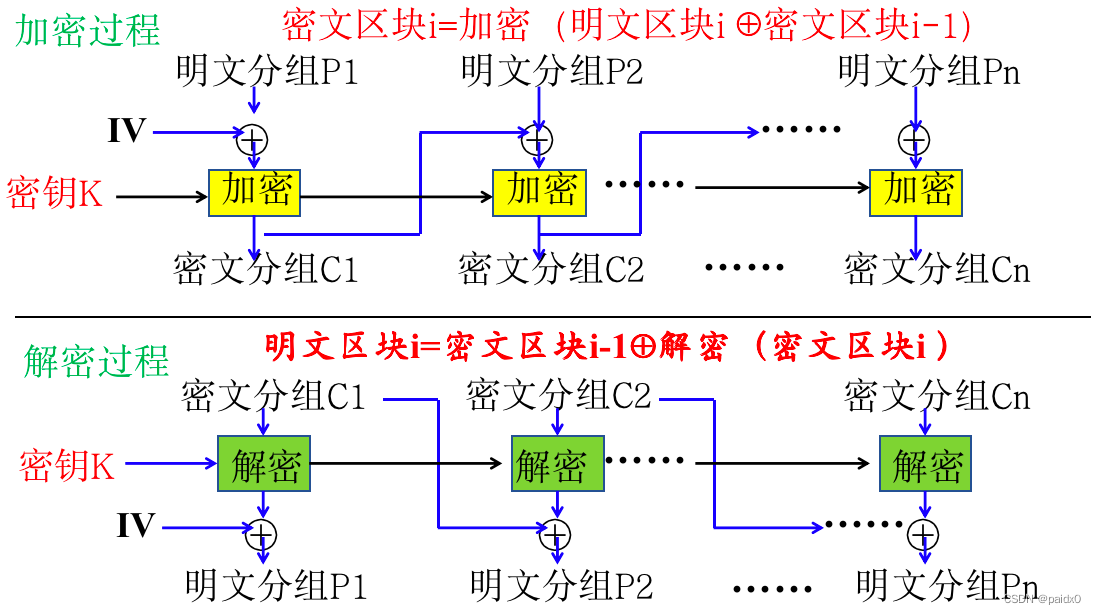
CBC分组链接

反馈机制，密文不仅依赖明文，还依赖前面的密文分组
正确解密需要确保前面的每个密文分组都是正确的
密文分组中的比特错误传播影响到本组和下一组的解密

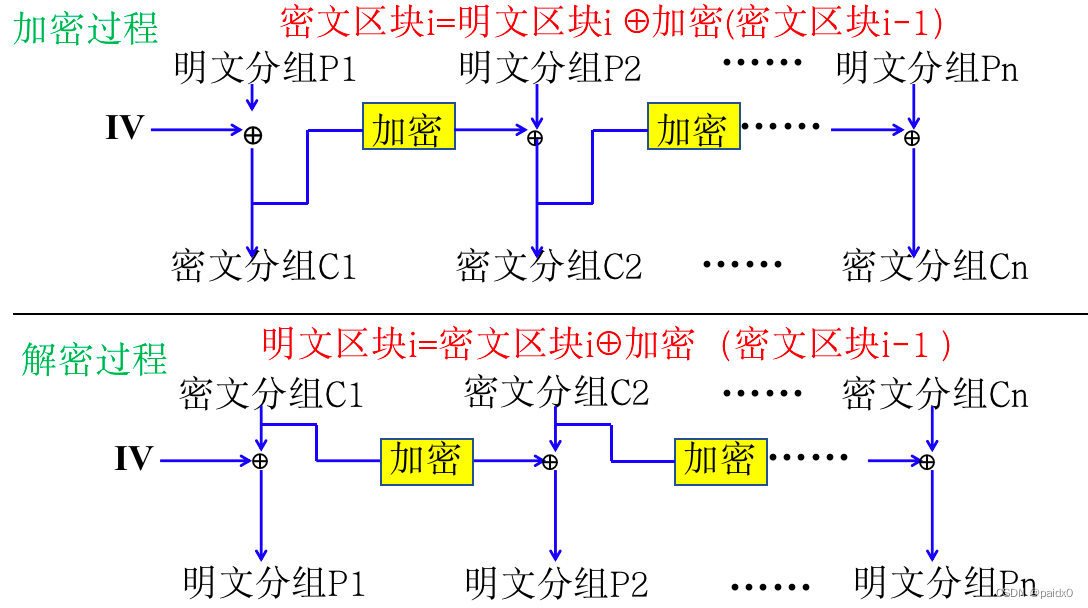
CFB密码反馈

对信道错误较敏感且造成错误传播
数据加解密的速率降低，其数据率不会太高
主要适用数据库加密、无线电通信或密文信号容易丢失出错的环境

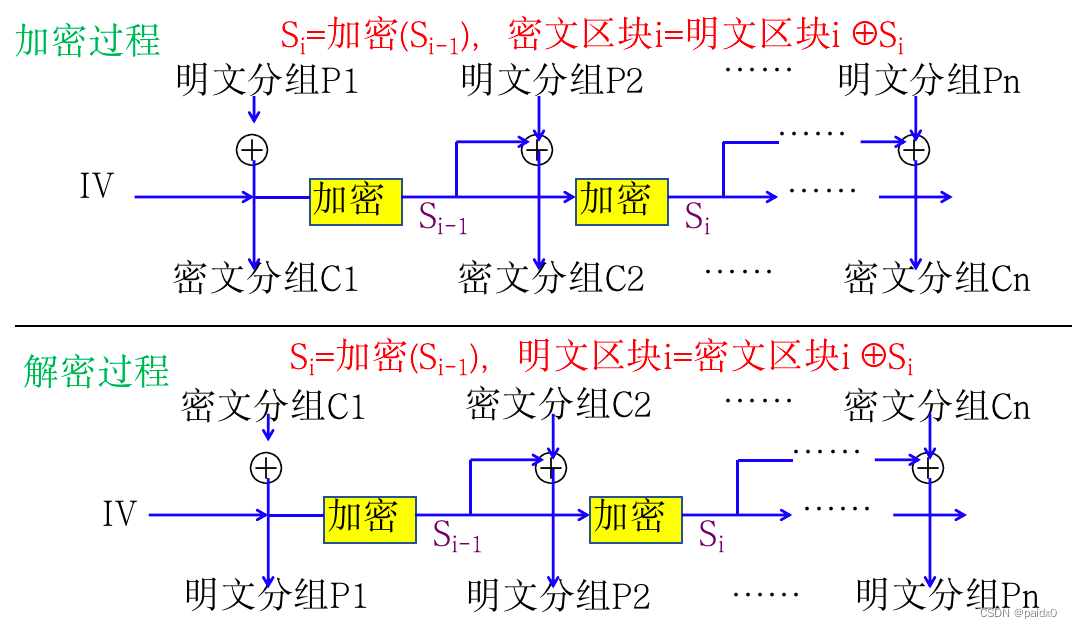
OFB输出反馈

克服错误传播带来的问题，但对密文被篡改难于检测
不具有自同步，需要保持严格的同步

序列密码

A5-1算法

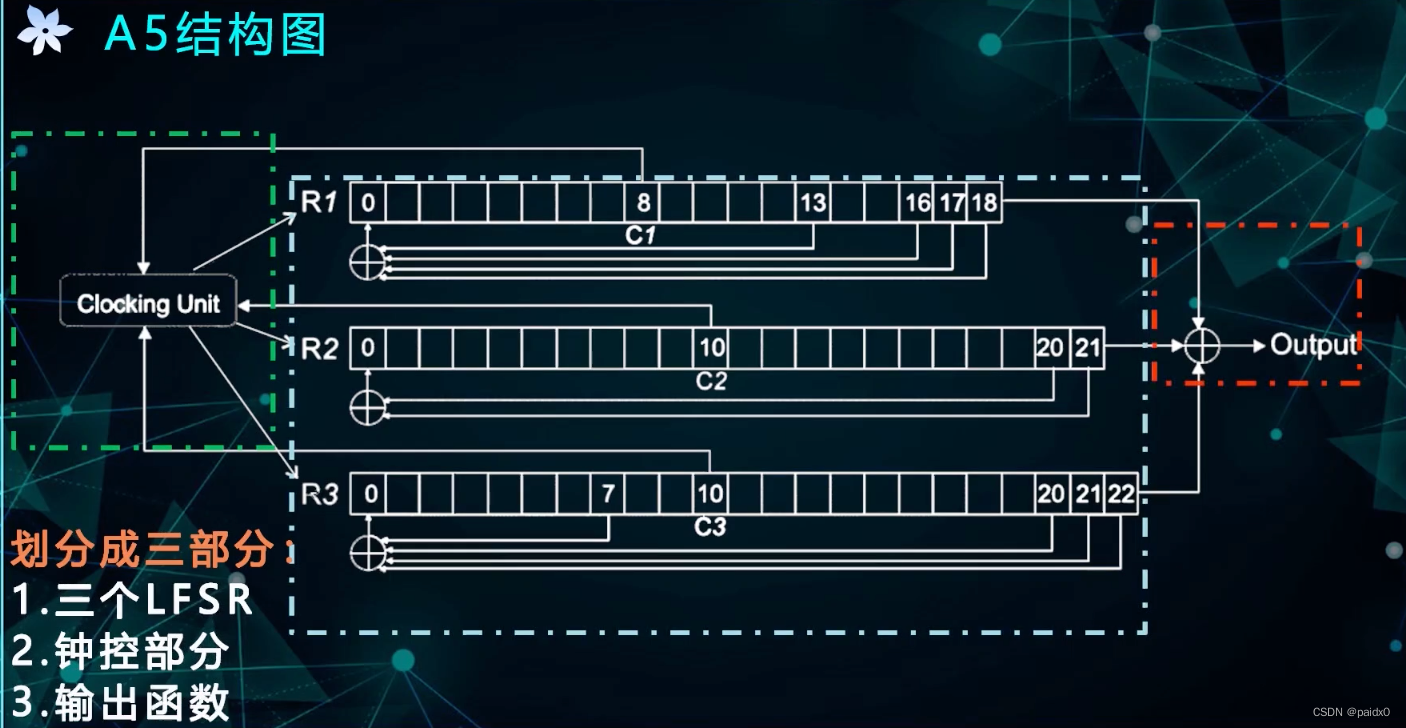
# 三个反馈序列LFSR，长度19、22、23

a1= [18]⨁[17]⨁[16]⨁[13]
a2= [21]⨁[20]
a3= [22]⨁[21]⨁[