数据结构与算法——串与数组篇详解

1. 串与数组

1.1 串概述

• 串，也称为字符串，是一个种特殊的线性表，由n（n>=0）个字符组成的有序序列。

• 名词解释

  • 长度：包含的字符个数n。
  • 空串：n为0的串就是空串，不包含任何字符。
  • 空白串：包含一个及以上（n>=1）空白字符的串，长度为空白字符的个数。
  • 子串：串中任意连续的字符组成的子序列。
    • 空串是任意串的子串。
    • 任意串是其自身的子串。“ABC”
  • 主串：包含子串的串。
  • 序号值：在之前的学习过程中称为“索引值”，字符在串中的位置。
  • 子串在主串中的位置：子串在主串中首次出现时的第一个字符在主串中的位置。
  • 串相等：两个串的长度相同，且各个对应位置的字符相同。

• 串的抽象类型（接口）

  public interface IString{
      public void clear();		//串的清空
      public boolean isEmpty();	//是否为空
      public int length();		//串的长度，串中字符的个数
      public char charAt(index);	//返回第index个字符值
      public IString substring(begin,end);	//*获得子串[begin,end)
      public IString insert(offset, str);		//在第offset个字符之前插入str串
      public IString delete(begin, end);		//删除子串[begin,end)
      public IString concat(IString str);		//*把str串连接到当前串的后面
      public int compareTo(IString str);		//串的比较，相同返回0，否则返回正/负
      public int indexOf(str, begin);		//从start开始，返回str在串中位置，不存在返回-1
  }
  

1.2 串的存储

• 串的存储结构包括：顺序存储 和 链式存储。

  • 顺序存储：使用数组存放字符。

    public class SeqString implements IString{
        private char[] strvalue;		// 字符数组，用于存放字符串信息
        private int curlen;				// 串的长度 current length
    }
    

  • 链式存储：使用链表存储。

    • 字符链表：每个结点只有一个字符的链表。

      

    • 块链表：每个结点可以有多个字符。

      

1.3 顺序串

1.3.1 算法：基本功能（了解）

public class SeqString implements IString{
    private char[] strvalue;		// 字符数组，用于存放字符串信息
    private int curlen;				// 串的长度 current length
    
    public void clear() {			//清空
        this.curlen = 0;
    }
    public boolean isEmpty() {		//是否有空
        return this.curlen == 0;
    }
    public int length() {			//串的长度
        return this.curlen;
    }
    public char charAt(int index) {
        if(index < 0 || index >= curlen) {
            throw new 字符串索引越界异常();	//String Index OutOfBounds Exception
        }
        return strvalue[index];
    }
}

1.3.2 算法：扩容

/**
* @param newCapacity 新容器大小
*/
public void allocate(int newCapacity) {
    char[] temp = strvalue;					// 存放原来的数据 ab数组
    strvalue = new char[newCapacity];		// 给strValue重新赋一个更大数组的值
    for(int i = 0; i < temp.length; i++) {	// 拷贝数据
        strvalue[i] = temp[i];
    }
}

1.3.3 算法：求子串

• 需求：“abcd”.substring(1,3) --> “bc”

  

public IString substring(int begin , int end) {
    // 1 两个参数校验
    if(begin < 0) {			// 1.1 begin 不能小于0
        throw new StringIndexOutOfBoundsException("begin不能小于0");
    }
    if(end > curlen) {		// 1.2 end 不能大于当前长度
        throw new StringIndexOutOfBoundsException("end不能大于当前长度");
    }
    if(begin > end) {		// 1.3 
        throw new StringIndexOutOfBoundsException("begin不能大于end");
    }
    
    // 2 优化：当前串直接返回
    if(begin == 0 && end == curlen) {
        return this;
    } 
    
    // 3 核心算法
    char[] buffer = new char[end - begin];			// 构建新数组
    for(int i = 0 ; i < buffer.length ; i ++) {		// 依次循环遍历新数组，一个一个赋值
        buffer[i] = strvalue[i + begin];
    }
    return new SeqString(buffer);					// 使用字符数组构建一个新字符串
}

1.3.4 算法：插入

/**  "abcdef".insert(2,"123").insert(...)
* @param offset 偏移量，插入的位置
* @param str 插入数据
*/
public IString insert (int offset, IString str) {
    //1 校验
    if(offset < 0 || offset > curlen) {
        throw new StringIndexOutOfBoundsException("插入位置不合法");
    }
    //2 兼容：如果容器不够，需要扩容   当前长度 + 新字符串 > 容器长度
    int newCount = curlen + str.length();
    if( newCount > strvalue.length ) {
        allocate(newCount);		//扩容结果就是刚刚好，没有额外空间
    }
    // 3 核心
    //3.1 核心1：从offset开始向后移动 str长度 个字符
    for(int i = curlen-1 ; i >= offset ; i --) {
        strvalue[i + str.length() ] = strvalue[i];
    }
    //3.2 核心2：依次插入
    for(int i = 0; i < str.length() ; i ++) {
        strvalue[i + offset] = str.charAt(i);
    }
    //3.3 设置数组长度
    this.curlen = newCount;
    return this;
}

1.3.5 算法：删除

/**
* @param begin 删除开始位置(含)
* @param end 删除结果位置(不含)
*/
public IString delete(int begin , int end) {
    // 1 校验
    // 1.1 begin 范围
    if(begin < 0) {
        throw new StringIndexOutOfBoundsException("begin不能小于0");
    }
    // 1.2 end 范围
    if(end > curlen) {
        throw new StringIndexOutOfBoundsException("end不能大于串长");
    }
    // 1.3 关系
    if(begin > end) {
        throw new StringIndexOutOfBoundsException("begin不能大于end");
    }
    
    // 2 核心：将后面内容移动到签名
    // 2.1 移动
    for(int i = 0 ; i < curlen - end ; i ++) {
        strvalue[i + begin] = strvalue[i + end];
    }
    // 2.2 重新统计长度  (end-begin 需要删除串的长度)
    curlen = curlen - (end-begin)
    return this;
}

1.3.6 算法：比较

/**
* @param str 需要比较的串
* return 
* 	>0 : 前面串值的值大于后面串
*   =0 : 前面串值的值等于后面串
*   <0 : 前面串值的值小于后面串
*/
public int compareTo(SeqString str) {
    int n = Math.min(curlen, str.curnlen) ; 	// 获得最短串的长度
    int k = 0 ;									// 循环遍历k
    char[] s1 = strvalue;
    char[] s2 = str.strvalue;
    while(k < n) {
        if(s1[k] != s2[k]) {					// 处理前缀不一致
            return s1[k] - s2[k];
        }
        k++;
    }
    return curlen - str.curlen;					// 两个串的前缀相等
}

1.4 模式匹配【难点，了解】

1.4.1 概述

• 串的查找定位操作，也称为串的模式匹配操作。
  • 主串：当前串，长度用n表示。
  • 模式串：在主串中需要寻找的子串，长度用m表示。
• 模式匹配特点：
  • 匹配成功，返回模式串的首字母在主串中的位序号（索引号）。
  • 匹配失败，返回-1
• 模式匹配的常见算法：
  • Brute-Force算法：蛮力算法，依次比较每一个，比较次数多，时间复杂度O(n×m)
  • KMP算法：滑动算法，比较的次数较少，时间复杂度O(n+m)

1.4.2 Brute-Force算法：分析

• 第一趟：运行后的结果

​

• 第一趟过渡到第二趟

  

• 第二趟不匹配，直接过渡到第三趟

  

• 第三趟：

  

• 第三趟过渡到第四趟

  

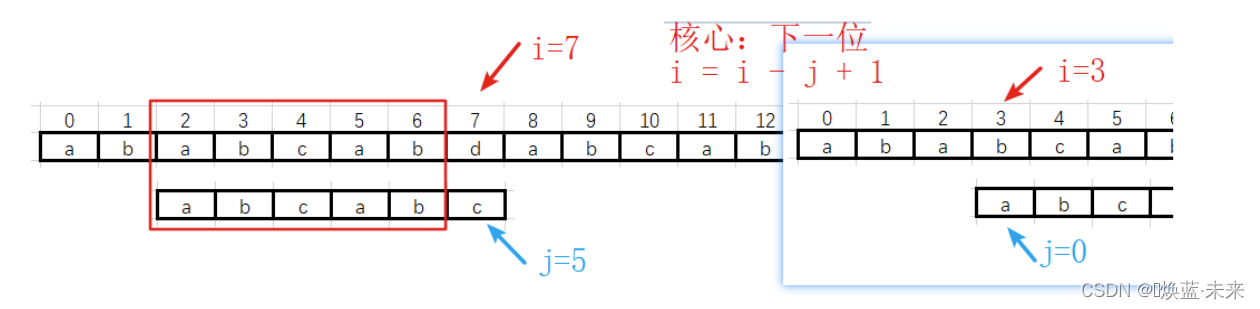
• 总结：核心算法（找主串的下一位）

  

1.4.3 Brute-Force算法：算法实现

/** this 主串
* @param t 模式串
* @param start 在主串中开始位置，例如：indexOf_BF("abcabc", 0)
*/
public int indexOf_BF(IString t, int start) {
    // 0.1 非空校验
    if(this == null || t == null) {				//0.1 主串或模式串为空
        return -1;
    }
    // 0.2 范围校验
    if(t.length() == 0 || this.length() < t.length()) {	//0.2模式串为空或比主串长
        return -1;
    }
    int i = start , j = 0;						// 1 声明变量
    while( i<this.length() && j<t.length() ) {	// 2 循环比较,主串和模式串都不能超过长度
        if(this.charAt(i) == t.charAt(j)) {		// 2.1 主串和模式串依次比较每一个字符
            i++;
            j++;
        } else {								// 2.2 当前趟过渡到下一趟
            i = i - j + 1;						// 2.3 核心算法：主串中下一字符
            j = 0;								// 2.4 模式串归零
        }
    }
    											// 3 处理结果
    if(j >= t.length()) {						//3.1 模式串已经循环完毕
        return i - t.length();					//3.2 匹配成功，第一个字母的索引号
    } else {
        return -1;								//3.3 匹配失败
    }
}

1.4.4 KMP算法：动态演示

• 核心思想：主串的指针i不会回退，通过滑动模式串进行匹配。

  • 滑动的原则：可以从最大公共前缀，直接跳到最大公共后缀。

• 思考：ababa 最大公共前后缀是？

  • 最大公共前缀：ababa
  • 最大公共后缀：ababa

• 第一趟：i 从 0–>2

  

• 遇到不匹配的数据时，需要移动模式串，当前公共部分是“ab”，没有最大公共前后缀。模式串从头开始

  

• 第二趟：i 从 2 --> 7

  

• 遇到不匹配的数据时，需要移动模式串，当前公共部分是“abcab”，有最大公共前后缀

  

• 第三趟： i=7 位置数据不一致

​

• 遇到不匹配的数据时，需要移动模式串，当前公共部分是“ab”，没有最大公共前后缀。模式串从头开始

  

• 第4趟：数据不一致，i 7 --> 8 ， j 归零

  

• 第五趟：i从8 --> 13

  

1.4.5 KMP算法：求公共前后缀 next数组 – 推导

• 当我们准备求公共前后缀时，主串和模式串具有相同的内容，所以只需要看模式串。
• 实例1：模式串：“abcabc”
• 提前将模式进行处理（预判）：将每一个字符假设不匹配时，公共前后缀提前记录下来，形成一个表格。
  • 第一个位置：-1
  • 第二个位置：0
  • 使用next数组，记录统计好的表格。

$$\begin{array}{ccccccc}模式串& a& b& c& a& b& c\\ j& 0& 1& 2& 3& 4& 5\\ next[j]& -1& 0& 0& 0& 1& 2\end{array}\text{\hspace{1em}(KMP next表格)}$$

• 实例2：“ababaaa”

$$\begin{array}{cccccccc}模式串& a& b& a& b& a& a& a\\ j& 0& 1& 2& 3& 4& 5& 6\\ next[j]& -1& 0& 0& 1& 2& 3& 1\end{array}\text{\hspace{1em}(KMP next表格)}$$

• 实例3：“ababaab”
  $$\begin{array}{cccccccc}模式串& a& b& a& b& a& a& b\\ j& 0& 1& 2& 3& 4& 5& 6\\ next[j]& -1& 0& 0& 1& 2& 3& 1\end{array}\text{\hspace{1em}(KMP next表格)}$$

1.4.6 KMP算法：求公共前后缀 next数组 – 算法演示

• 实例1：模式串：“abcabc”
  $$\begin{array}{ccccccc}模式串& a& b& c& a& b& c\\ j& 0& 1& 2& 3& 4& 5\\ next[j]& & & & & & \end{array}\text{\hspace{1em}(KMP next表格)}$$

  • 第三位的数值

    

  • 第四位的数值

    

  • 第五位的数值

    

  • 第六位的数值

    

  • 处理完成

    

• 实例2：“ababaaa”
  $$\begin{array}{cccccccc}模式串& a& b& a& b& a& a& a\\ j& 0& 1& 2& 3& 4& 5& 6\\ next[j]& -1& 0& & & & & \end{array}\text{\hspace{1em}(KMP next表格)}$$

  • 第三位的值： k == 0

    

  • 第四位的值：字符相等

    

  • 第五位的值： 字符相等

    

  • 第六位的值：字符相等

    

  • 第七位的值：字符不相等，且k!=0

    • 字符不相等，k!=0，移动k

      

    • 字符不相等，k!=0，再移动k

      

    • 字符相等

      

  • 处理完成

    

1.4.7 KMP算法：求公共前后缀 next数组 – 算法

/** 获得next数组
* @param T 模式串
* return 返回next数组
*/
public int[] getNext(IString T) {
    //1. 创建数组，与模式串字符个数一致
    int[] next = new int[T.length()]; 		
    int j = 1;								// 串的指针
    int k = 0;								// 模式串的指针（相同字符计数器）
    // 2 默认情况
    next[0] = -1;							
    next[1] = 0;
    // 3 准备比较
    while( j < T.length() -1 ) {			// 比较倒数第二个字符
        if(T.charAt(j) == T.charAt(k)) {	// 连续有字符相等
            next[j+1] = k+1;
            j++;
            k++;
        } else if (k == 0) {
            next[j+1] = 0;
            j++;
        } else {		//k不是零
            k = next[k];				//p119 数学推导
        }
    }
    // 4 处理完成，返回数组
    return next;
}

• 处理字符相同

• 处理字符不相等，且k==0

1.4.8 KMP算法：next数组使用

• 主串：ababababaaa

• 模式串：ababaaa

  • next数组
    $$\begin{array}{cccccccc}模式串& a& b& a& b& a& a& a\\ j& 0& 1& 2& 3& 4& 5& 6\\ next[j]& -1& 0& 0& 1& 2& 3& 1\end{array}\text{\hspace{1em}(KMP next表格)}$$

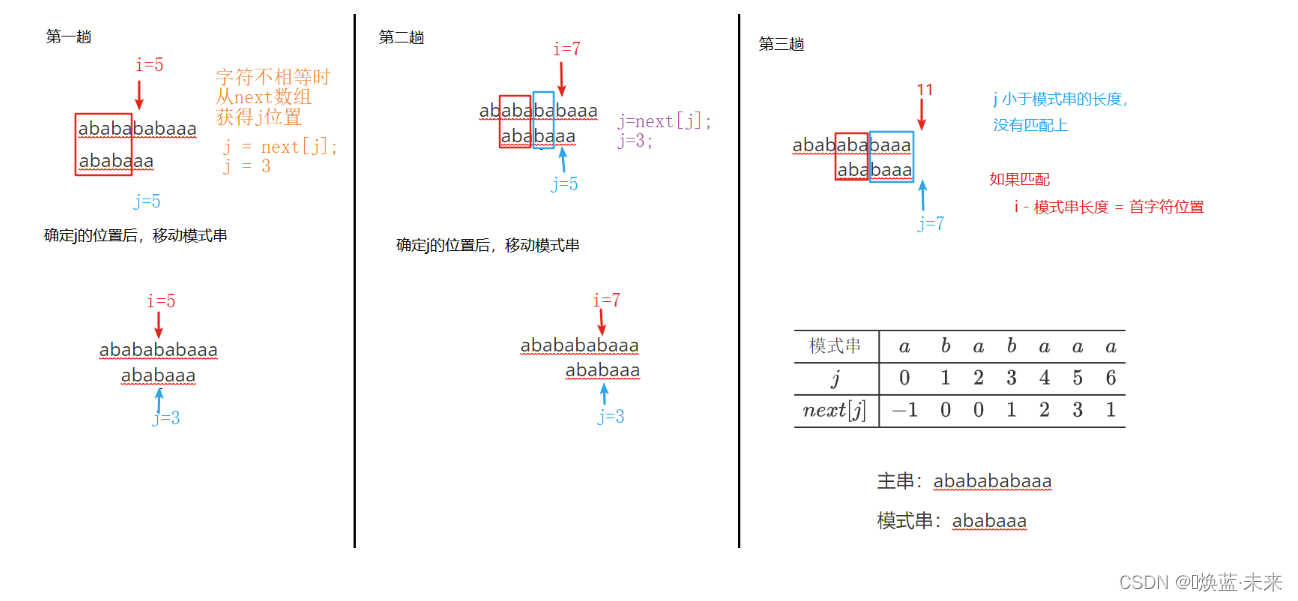
1.4.9 KMP算法

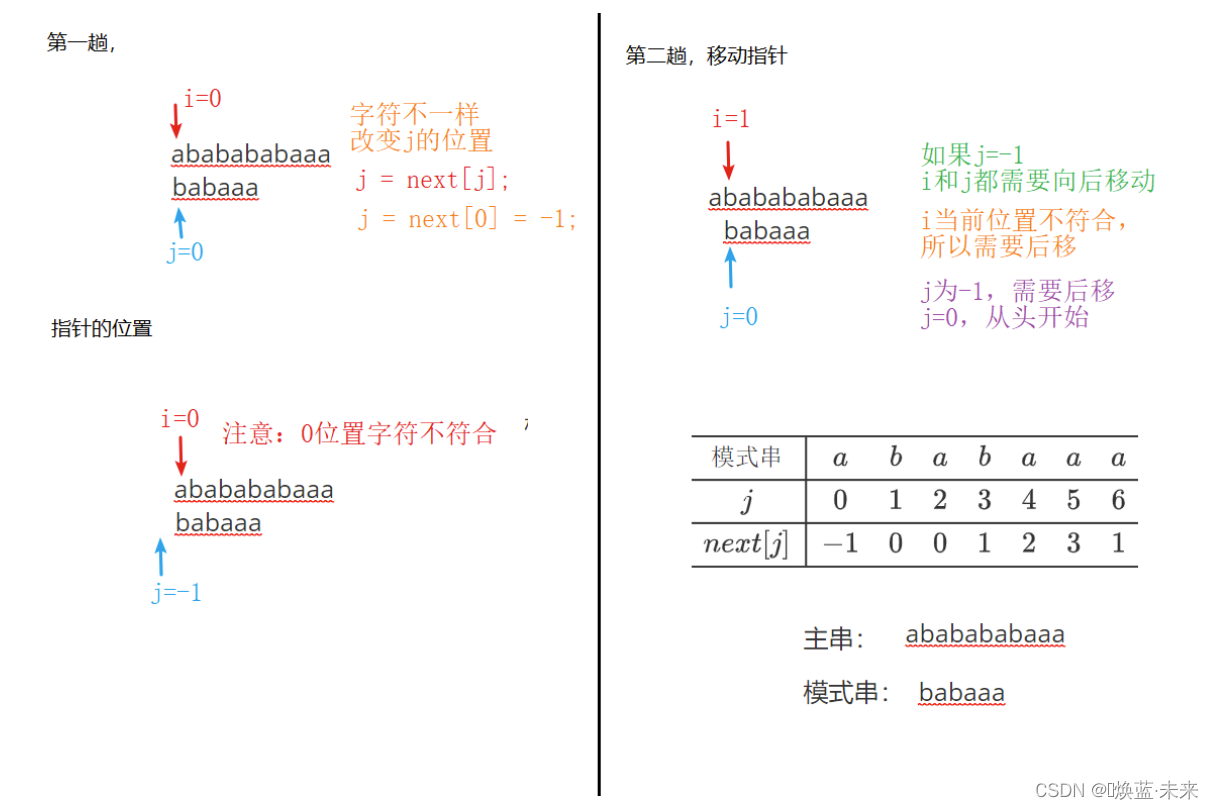
/** this 当前串，也就是主串 (this.length() 主串长度)
* @param T 模式串 (T.length() 模式串长度)
* @param start 从主串中开始位置，例如："abaababaaa".index_KMP("ababaaa",0);
*/
public int index_KMP(IString T, int start) {
    //1 准备工作：next数组、指针
    int[] next = getNext(T);			//1.1 获得模式的next数组
    int i = start;						//1.2 主串指针
    int j = 0;							//1.3 模式串的指针
    //2 字符比较移动
    while(i<this.length() && j<T.length()) {	//2.1 串小于长度
        if(j == -1 || 							//2.2.1 第一个字符不匹配，直接跳过
           		this.charAt(i) == T.charAt(j)) {//2.2.2 字符匹配
            i++;
            j++;
        } else {
            j = next[j];						//2.3 移动模式串
        }
    }
    //3 处理结果
    if(j < T.length()) {				//3.1 移动位置没有模式串长，不匹配
        return -1;
    } else {
        return i - T.length();			//3.2 匹配，目前在串后面，需要移动首字符
    }
}

1.5 数组

1.5.1 概述

• 数组：一组具有相同数据类型的数据元素的集合。数组元素按某种次序存储在一个地址连续的内存单元空间中。

• 一维数组：一个顺序存储结构的线性表。[a0,a1,a2, …]

• 二维数组：数组元素是一维数组的数组。[ [] , [] , [] ] 。二维数组又称为矩阵。
  $$A_{n\times m}=\left[\begin{array}{cccc}{a}_{0,0}& a_{0,1}& \cdots & a_{0,m-1}\\ a_{1,0}& a_{1,1}& \cdots & a_{1,m-1}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n-1,0}& a_{n-1,1}& \cdots & a_{n-1,m-1}\end{array}\right]\text{\hspace{1em}(二维数组的矩阵表示)}$$

1.5.2 数组的顺序存储（一维）

• 多维数组中，存在两种存储方式：

  • 以行序为主序列的存储方式（行优先存储）。大部分程序都是按照行序进行存储的。
  • 以列序为主序列的存储方式（列优先存储）

• 一维数组内存地址

  • Loc(0) ：数组的首地址
  • i ： 第i个元素
  • L ：每一个数据元素占用字节数
    

1.5.3 数组的顺序存储（二维）

1）行序

• 行序：使用内存中一维空间（一片连续的存储空间），以行的方式存放二维数组。先存放第一行，在存放第二行，依次类推存放所有行。

  

• 二维数组（n×m）内存地址（以行序为主序列）

  • Loc(0,0) ：二维数组的首地址
  • i ： 第i个元素
  • L ： 每一个数据元素占用字节数
  • m：矩阵中的列数

  $$Loc(i,j)=Loc(0,0)+(i\times m+j)\times L(0\le i\le n-1,0\le j\le m-1)\text{\hspace{1em}()}$$

• 注意：

  • 如果索引号不是从0开始，不能使用此公式。
  • 如果索引号不是从0开始的，需要先将索引号归零，再使用公式。

  

2）列序

• 列序：使用内存中一维空间（一片连续的存储空间），以列的方式存放二维数组。先存放第一列，再存放第二列，依次类推，存放所有列。

  

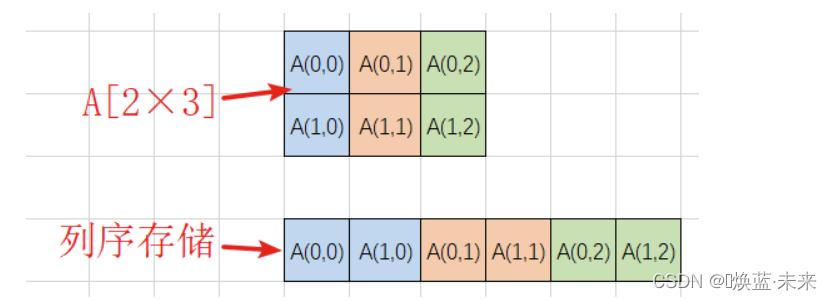
• 二维数组（n×m）内存地址（以列序为主序列）
  $$Loc(i,j)=Loc(0,0)+(j\times n+i)\times L(0\le i\le n-1,0\le j\le m-1)\text{\hspace{1em}()}$$

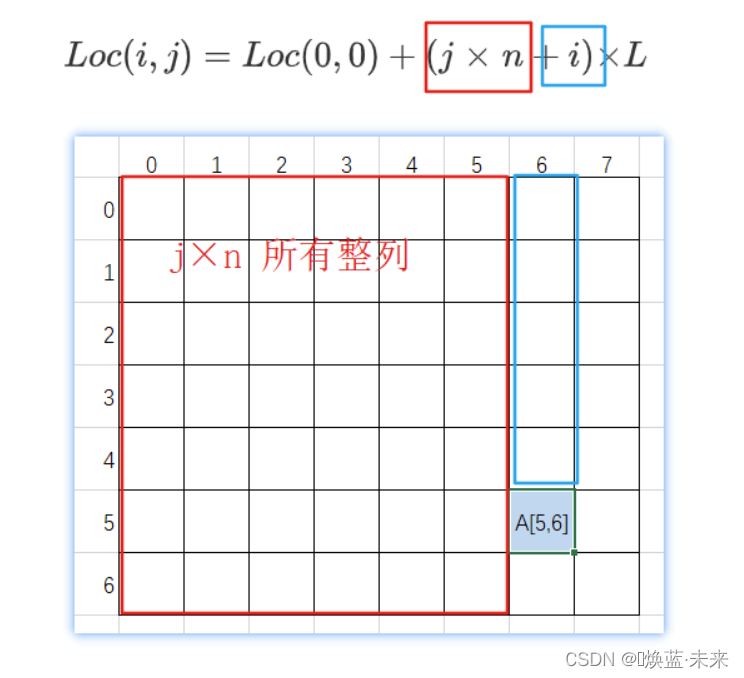
3）练习

• 实例1：

  有一个二维数组A[1…6,0…7]，每一个数组元素用相邻的6个字节存储，存储器按字节编址，那么这个数组占用的存储空间大小是（ D ）个字节。

  A. 48

  B. 96

  C. 252

  D. 288

​

• 实例2：

  设有数组A[1…8,1…10]，数组的每个元素占3字节，数组从内存首地址BA开始以列序为主顺序存放，则数组元素A[5,8]的存储首地址为（ ）。

  A. BA + 141

  B. BA + 180

  C. BA + 222

  D. BA + 225

A[1..8,1..10]  --> A[8×10] 			//先行后列

• 例如3：

设有数组A[0…8,1…10]，数组的每个元素占5字节，数组从内存首地址BA开始以列序为主顺序存放，则数组元素A[7,8]的存储首地址为（ BA + 350 ）。

A[0..8,1..10]   --> A[9×10]

1.5.4 特殊矩阵概述

• 特殊矩阵：具有相同的数据或0元素，且数据分布具有一定规律。
• 分类：
  • 对称矩阵
  • 三级矩阵
  • 对角矩阵
• 特殊矩阵只有部分有数据，其他内容为零，使用内存中一维空间（一片连续的存储空间）进行存储时，零元素没有必要进行存储，通常都需要进行压缩存储。
• 压缩存储：多个值相同的矩阵元素分配同一个存储空间，零元素不分配存储空间。
  • 存储有效数据，零元素和无效数据不需要存储。
  • 不同的举证，有效和无效定义不同。

1.5.5 对称矩阵压缩存储【重点】

1）定义及其压缩方式

• 什么是对称矩阵：a(i,j) = a(j,i)
  $$\left[\begin{array}{cccc}0& 1& 0& 0\\ 1& 0& 1& 1\\ 0& 1& 0& 0\\ 0& 1& 0& 0\end{array}\right]\text{\hspace{1em}(对称矩阵)}$$

• 对称矩阵的压缩方式：共4种

  1. 下三角部分以行序为主序存储的压缩【学习，掌握】

     

  2. 下三角部分以列序为主序存储的压缩

     

  3. 上三角部分以行序为主序存储的压缩

     

  4. 上三角部分以列序为主序存储的压缩

     

• n×n对称矩阵压缩 n (n+1) / 2 个元素，求 1+2+3+…+n的和，只需要计算三角中的数据即可

  

$$\left[\begin{array}{cccc}{a}_{0,0}& 0& 0& 0\\ a_{1,0}& a_{1,1}& 0& 0\\ a_{2,0}& a_{2,1}& a_{2,2}& 0\\ a_{3,0}& a_{3,1}& a_{3,2}& a_{3,3}\end{array}\right]\text{\hspace{1em}(对称矩阵)}$$

2）压缩存放及其公式

• 压缩后存放到一维空间（连续的存放空间中）
  

• 对称矩形 A(i,j) 对应 一维数组 s[k] , k与i和j 公式：
  $$k=\{\begin{array}{ll}\frac{i(i+1)}{2}+j& \text{(i}\ge \text{j)}\\ \frac{j(j+1)}{2}+i& \text{(i<j)}\end{array}\text{\hspace{1em}(对称矩阵压缩存储公式)}$$

3）练习

• 练习1：

  

a(8,5)  -->索引库1,1表示方式
需要将1,1转化成0,0方式，从而可以使用公式，i和j同时-1
a(7,4)  -->索引库0,0表示方式
因为：i >= j
k= i(i+1)/2 +j = 7 * 8 / 2 + 4 = 32
32为索引为0的一维数组的下标
数据b下标是从1开始，对应的下标 32+1=33

• 练习2：

b[13] 下标从1开始，归零
b[12] 下标从0开始，k=12
i*(i+1)/2 , 如果i=4，结果为10
12-10 = j
下标0,0时，a(4,2)
下标1,1时，a(5,3)

1.5.6 三角矩阵

1）概述&存储方式

• 三角矩阵分为：上三角矩阵、下三角矩阵

  • 上三角矩阵：主对角线（不含主对角线）下方的元素值均为0。只在上三角的位置进行数据存储

    

  • 下三角矩阵：主对角线（不含主对角线）上方的元素值均为0。只在下三角的位置进行数据存储

    

• 存储方式：三角矩阵的存放方式，与对称矩阵的存放方式相同。

2）上三角矩阵

• 上三角矩阵实例

$$\left[\begin{array}{cccc}{a}_{0,0}& a_{0,1}& \cdots & a_{0,n-1}\\ 0& a_{1,1}& \cdots & a_{1,n-1}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & a_{n-1,n-1}\end{array}\right]\text{\hspace{1em}(上三角矩阵)}$$

• 上三角矩阵对应一维数组存放下标，计算公式
  $$k=\{\begin{array}{ll}空& \text{(i>j)}\\ \frac{j(j+1)}{2}+i& \text{(i}\le \text{j)}\end{array}\text{\hspace{1em}(上三角矩阵公式)}$$

3）下三角矩阵

• 下三角矩阵实例

$$\left[\begin{array}{cccc}{a}_{0,0}& 0& \cdots & 0\\ a_{1,0}& a_{1,1}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ a_{n-1,0}& a_{n-1,1}& \cdots & a_{n-1,n-1}\end{array}\right]\text{\hspace{1em}(下三角矩阵)}$$

• 下三角矩阵对应一维数组存放下标，计算公式
  $$k=\{\begin{array}{ll}\frac{i(i+1)}{2}+j& \text{(i}\ge \text{j)}\\ 空& \text{(i<j)}\end{array}\text{\hspace{1em}(下三角矩阵压缩公式)}$$

1.5.7 对角矩阵

1） 定义&名词

• 对角矩阵：矩阵的所有非零元素都集中在以主对角线为中心的带状区域中，即除主对角线上和直接在主对角线上、下方若干条对角线上的元素之外，其余元素皆为零。

  

• 名词：

  • 半带宽：主对角线一个方向对角线的个数，个数为d。

  • 带宽：所有的对角线的个数。个数为 2d+1

  • n阶2d+1对角矩阵非零元素个数：n(2d+1) - d(d+1)

    • n(2d+1) ：下图中所有颜色的个数
    • d(d+1)/2 ：右下方浅蓝色三角的个数
    • d(d+1) ：2个三级的个数（右下方、左上方）

    

  • 一维数组存储个数：n(2d+1) ，若某行没有2d+1个元素，则0补足。

2）压缩存储

$$A[5\times 5]=\left[\begin{array}{ccccc}{a}_{0,0}& a_{0,1}& 0& 0& 0\\ a_{1,0}& a_{1,1}& a_{1,2}& 0& 0\\ 0& a_{2,1}& a_{2,2}& a_{2,3}& 0\\ 0& 0& a_{3,2}& a_{3,3}& a_{3,4}\\ 0& 0& 0& a_{4,3}& a_{4,4}\end{array}\right]\text{\hspace{1em}(对角矩阵)}$$

• 压缩后存放一维数组，第一行和最后一行不够2d+1，所以需要补零。

$$Loc(i,j)=Loc(0,0)+[i(2d+1)+d+(j-i)]\times L\text{\hspace{1em}(对角矩阵公式)}$$

1.6 稀疏矩阵

1.6.1 定义&存储方式

• 稀疏矩阵：具有较多的零元素，且非零元素的分布无规律的矩阵。
  $$A[5\times 6]=\left[\begin{array}{cccccc}0& 0& 8& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 5& 0& 0& 0& 16& 0\\ 0& 0& 18& 0& 0& 0\\ 0& 0& 0& 9& 0& 0\end{array}\right]\text{\hspace{1em}(系数矩阵)}$$

  • 稀疏因子：用于确定稀疏矩阵个数指标

• 常见的2种存放方式：三元组表存储、十字链表存储

1.6.2 三元组表存储

1） 概述

• 使用三元组唯一的标识一个非零元素
• 三元组组成：row行、column列、value值
• 三元组表：用于存放稀疏矩阵中的所有元素。

2）相关类及其操作

• 三元组结点类

  public class TripleNode {	//三结点
      public int row;			//行号
      public int column;		//列号
      public int value;		//元素值
  }
  

• 三元组顺序表类：

  public class SparseMatrix {			//稀疏矩阵
      public TripleNode[] data;		//三元组表
      public int rows;				//行数n
      public int cols;				//列数m
      public int nums;				//非零元素的个数
  }
  

• 三元组表初始化操作：

1.6.3 三元组表存储：矩阵转置

1）定义

• 矩阵转置：一种简单的矩阵运算，将矩阵中每个元素的行列序号互换。
  • 特点：矩阵N[m×n] 通过转置 矩阵M[n×m]
  • 转置原则：转置前从左往右查看每一列的数据，转置后就是一行一行的数据。

$$\begin{array}{cccccc}& 0& 1& 2& 3& 4\\ 转置前& a_{0,2,8}& a_{2,0,5}& a_{2,4,16}& a_{3,2,18}& a_{4,3,9}\\ & & & & & \\ 转置后& a_{0,2,5}& a_{2,0,8}& a_{2,3,18}& a_{3,4,9}& a_{4,2,16}\end{array}\text{\hspace{1em}(a(row,column,value))}$$

2）算法分析

3）算法：转置（了解）

/** this转置前的对象，每一个对象中都有一个data数据
*   tm 转置后的对象，每一个对象中都有一个data数据
* return 转置后的稀疏矩阵对象
*/
public SparseMatrix transpose() {		//转置
    // 1 根据元素个数，创建稀疏矩阵
    SparseMatrix tm = new SparseMatrix(nums);
    // 2 设置基本信息
    tm.cols = rows;					//2.1 行列交换
    tm.rows = cols;					//2.2 列行交换
    tm.nums = nums;					//2.3 元素个数
    // 3 进行转置
    int q = 0;									//3.1 转置后数据的索引
    for(int col = 0 ; col < cols; col ++) {		//3.2 转置之前数据数组的每一个列号
        for(int p = 0; p < nums; p ++) {		//3.3 依次获得转置前数据数组的每一个数据
            if (data[p].column == col) {		//3.4 获得指定列的数据
                tm.data[q].row = data[p].column;	//3.5 行列交换，值不变
                tm.data[q].column = data[p].row;
                tm.data[q].value = data[p].value;
                q++;								//3.6 转置后的指针后移
            }
        }
    }
    // 4 返回转置后的稀疏矩阵
    return tm;
}

• 矩阵转置时间复杂度：O(n×t) ，n列数，t非零个数

1.6.4 三元组表存储：快速矩阵转置

1）定义

• 假设：原稀疏矩阵为N、其三元组顺序表为TN，N的转置矩阵为M，其对应的三元组顺序表为TM。
• 快速转置算法：求出N的每一列的第一个非零元素在转置后的TM中的行号，然后扫描转置前的TN，把该列上的元素依次存放于TM的相应位置上。
• 基本思想：分析原稀疏矩阵的数据,得到与转置后数据关系
  • 每一列第一个元素位置：上一列第一个元素的位置 + 上一列非零元素的个数
  • 当前列，原第一个位置如果已经处理，第二个将更新成新的第一个位置。

2）公式

• 需要提供两个数组：num[]、cpot[]
  • num[] 表示N中第col列的非零元素个数
  • cpot[] 初始值表示N中的第col列的第一个非零元素在TM中的位置
• 公式：

$$\begin{gathered} cpot[0]=0 \\ cpot[col]=cpot[col-1]+num[col-1] \\ \begin{array}{ccccccc}col& 0& 1& 2& 3& 4& 5\\ num& 1& 0& 2& 1& 1& 0\\ cpot& 0& 1& 1& 3& 4& 5\end{array}\text{\hspace{1em}(矩阵快速转置)} \end{gathered}$$

3）算法：快速转置（了解）

public SparseMatrix fasttranspose() {
    // 1 根据元素个数，创建稀疏矩阵
    SparseMatrix tm = new SparseMatrix(nums);
    // 2 设置基本信息
    tm.cols = rows;					//2.1 行列交换
    tm.rows = cols;					//2.2 列行交换
    tm.nums = nums;					//2.3 元素个数
    
    // 3 校验
    if(num <= 0) {
        return tm;
    }
    
    // 4 每一列的非零个数
    int num = new int[cols];			//4.1 根据列数创建num数组
    for(int i = 0; i<cols; i ++) {		//4.2 初始数据（可省略）
        num[i] = 0;
    }
    for(int i = 0; i< nums; i ++) {		//4.3 遍历转置的数据
        int j = data[i].column;
        num[j]++;
    }
    
    // 5 转置后每一列第一个元素的位置数组
    int cpot = new int[cols];			// 5.1 位置的数组
    cpot[0] = 0;						// 5.2 第一列第一个元素为0
    for(int i = 1; i < cols ; i ++) {
        cpot[i] = cpot[i-1] + num[i-1];	// 5.3 当前列第一个元素位置 = 上一列位置+个数
    }
    
    // 6 转置处理
    for(int i = 0 ; i < nums ; i ++) {
        int j = data[i].column;				//6.1 转置前，每一个元素的列数
        int k = cpot[j];					//6.2 转置后的位置
        tm.data[k].row = data[i].column;	//6.3 原数据 转置后 数据
        tm.data[k].column = data[i].row;
        tm.data[k].value = data[i].value;
        cpot[j]++;							//6.4 下一个元素的位置
    }
    
}

• 时间复杂度：O(n+t) ，n列数，t非零个数

1.6.5 十字链表存储

1）定义

• 当稀疏矩阵中非零元素的位置或个数经常发生变化时，不宜采用三元组顺序表存储结构，而该用链式存储结构。

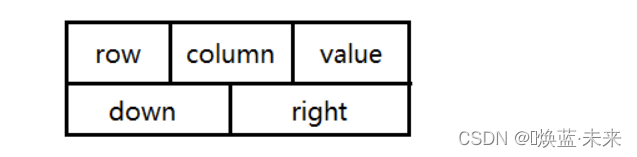
• 十字链表结点由5个域组成：

  • row：所在行

  • column：所在列

  • value：非零元素值

  • right：存放与该非零元素同行的下一个非零元素结点指针。

  • down：存放与该非零元素同列的下一个非零元素结点指针。

    

2）相关类

• 结点类：

  class OLNode {
      public int row, col;		//行号、列号
      public int value;			//元素值
      public OLNode right;		//行链表指针
      public OLNode down;			//列链表指针
  }
  

• 十字链表类：

  class CrossList {
      public int mu, nu, tu;			//行数、列数、非零元素个数
      public OLNode[] rhead, chead;	//行、列指针数组
  }
  

=========================================================

后记

好啦，以上就是本期全部内容，能看到这里的人呀，都是能人。

十年修得同船渡，大家一起点关注。

我是♚焕蓝·未来，感谢各位【能人】的：点赞、收藏和评论，我们下期见！

各位能人们的支持就是♚焕蓝·未来前进的巨大动力~

注：如果本篇Blog有任何错误和建议，欢迎能人们留言！